Baccalauréat STI2D Antilles Guyane 2013 - Correction Exercice 4
Page 8 sur 8
Exercice 4 6 points
Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par $f(x) = \dfrac{1}{x} - \ln x$. On appelle $\mathcal{C}_{f}$ sa courbe représentative dans un repère orthonormal $\left( {{\mathrm{O}};\vec i,\vec j} \right)$.
- Sur le graphique ci-dessous, on donne $\mathcal{C}_{f}$ et les courbes $C$ et $\Gamma$. L'une de ces deux courbes représente graphiquement la dérivée $f'$ de $f$, et l'autre une des primitives $F$ de $f$.
- Indiquer laquelle des deux courbes $C$ et $\Gamma$ représente graphiquement $f'$. Justifier. Sur le graphique on voit que $f$ est décroissante sur $]0~;~+ \infty[$ ; donc sur cet intervalle $f'(x) < 0$ : seuls les points de $\Gamma$ ont tous leurs ordonnées négatives .
- Par lecture graphique, donner $F(1)$. D'après la question précédente $C$ est la représentation graphique de l'une des primitives de $f$. On lit sur le graphe que le point de $C$ d'abscisse 1 a pour ordonnée 1. $F(1) = 1$.
$\Gamma$ est donc la représentation de $f'$.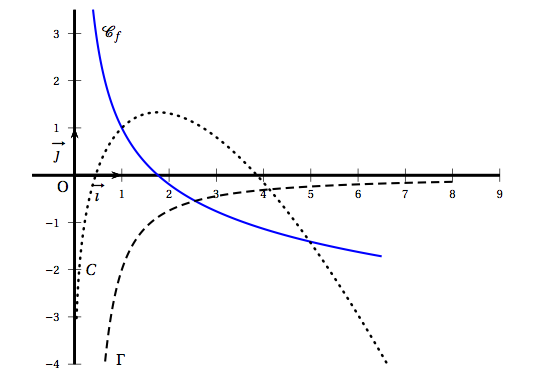
- Dans cette question, on pourra vérifier la cohérence des résultats obtenus avec les courbes représentatives données sur le dessin.
- Déterminer la limite de la fonction $f$ quand $x$ tend vers $0$. Interpréter graphiquement cette limite. On a pour $x > 0 , \: \displaystyle\lim_{x \to 0} \dfrac{1}{x} = + \infty$ et $\displaystyle\lim_{x \to 0} \ln x = - \infty$, donc par différence $\displaystyle\lim_{x \to 0} \dfrac{1}{x} - \ln x = + \infty$. Graphiquement ceci signifie que l'axe des ordonnées est asymptote verticale au graphe de $f$.
- Déterminer la limite de la fonction $f$ quand $x$ tend vers $+ \infty$. $\displaystyle\lim_{x \to + \infty} \dfrac{1}{x} = 0$ et $\displaystyle\lim_{x \to + \infty} - \ln x = - \infty$, donc par somme de limites, $\displaystyle\lim_{x \to + \infty} f(x) = - \infty$.
- Calculer $f'(x)$ et montrer que l'on peut écrire : $f'(x) = \dfrac{- x - 1}{x^2}$. Sur $]0~;~+ \infty[$, \:$f$ est dérivable et $f'(x) = - \dfrac{1}{x^2} - \dfrac{1}{x} = \dfrac{- 1 - x}{x^2} = - \dfrac{x + 1}{x^2} = \dfrac{- x - 1}{x^2}$.
- Étudier le signe de $f'(x)$ puis donner le tableau de variations de $f$. Comme $x^2 > 0$ pour $x > 0$, le signe de $f'(x)$ est celui du numérateur $- x - 1$.
$- x - 1 > 0 \iff - 1 > x \iff x < - 1$
et $- x - 1 < 0 \iff - 1 < x \iff x > - 1$.
Comme $x > 0$, la dérivée est donc négative et ceci confirme que la fonction $f$ est décroissante sur $]0~;~+ \infty[$. D'où le tableau de variations :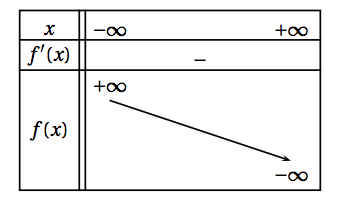
- Soit $H$ la fonction définie sur $]0~;~+ \infty[$ par $H(x) = x - (x - 1) \ln x$.
- Montrer que $H$ est une primitive de $f$ sur $]0~;~+ \infty[$. On a $H'(x) = 1 - 1\ln x - (x - 1) \times \dfrac{1}{x} = 1 - \ln x - 1 + \dfrac{1}{x} = \dfrac{1}{x} - \ln x = f(x).$ $H$ est donc une des primitives de $f$.
- En déduire l'expression de la fonction $F$ de la question 1. On a $H(1) = \dfrac{1}{1} - \ln 1 = 1$ et on a vu que $F(1) = 1$, donc $F = H$ et $F(x) = x - (x - 1) \ln x$.
- Calculer $\displaystyle\int_{1}^{e} f(x)\:\mathrm{d}x$. On connaît une primitive de $f$ on peut donc calculer l'intégrale : $$\begin{array}{ll}\displaystyle\int_{1}^{\text{e}} f(x)\:\text{d}x &= \left[F(x) \right]_{0}^{\text{e}}\\& = F(\text{e}) - F(1) \\&= \text{e} - (\text{e} - 1) \ln \text{e} - \left[1 - (1 - 1) \ln 1 \right]\\& = \text{e} - (\text{e} - 1) - 1\\& = 1 - 1 \\&= 0\end{array}$$
- Vues: 17756
