Baccalauréat STI2D Antilles Guyane 2013 - Correction Exercice 3

Page 6 sur 8: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Nombres complexes

Le plan complexe est rapporté à un repère orthonormal direct $\left( {{\mathrm{O}};\vec u,\vec v} \right)$. On note $\mathbb C$ l'ensemble des nombres complexes, et i le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$.

1. On considère l'équation (E) d'inconnue $z$ : \[(2 - i)z = 2 - 6i.\]
   1. Résoudre dans $\mathbb C$ l'équation (E). On notera $z_{1}$ la solution de (E) que l'on écrira sous forme algébrique.
   Rappel : Pour calculer le quotient de deux nombres complexes, on multiplie numérateur et dénominateur par le conjugué du dénominateur. $$\begin{array}{lll} (2 - i)z = 2 - 6i&\iff z = \dfrac{2-6i}{2-i}&\\ &\iff z = \dfrac{(2-6i)(2+i)}{(2-i)(2+i)}& \\ &\iff z = \dfrac{4+2i-12i+6}{2^2+1^2}& \text{ car } z\overline{z}=a^2+b^2\\ &\iff z = \dfrac{10-10i}{5}& \\ &\iff z = 2-2i &\\ \end{array}$$
   L'équation (E) a pour ensemble de solution : $\mathcal{S}=\{2-2i\}$
   2. Déterminer la forme exponentielle de $z_{1}$.
   Forme trigonométrique de $z_1=2-2i$:
   Module : $|z_1|=\sqrt{a^2+b^2}=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}$
   Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{2}{2\sqrt{2}}= \dfrac{1}{ \sqrt{2}}= \dfrac{\sqrt2}{ 2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{-2}{2\sqrt{2}}=-\dfrac{\sqrt2}{ 2} \end{array} \right.$$ Ainsi $\theta=-\dfrac{\pi}{4}$ convient; on a donc: $$z_1=[2\sqrt{2};-\dfrac{\pi}{4}] \text{ ou } z_2=2\sqrt{2}\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$
   La forme exponentielle de $z_{1}$ est $z_1= 2\sqrt{2}e^{-i\frac{\pi}{4}}$
   3. Soit $z_{2}$ le nombre complexe défini par : $z_{2} = e^{- i\frac{\pi}{2}} \times z_{1}$. Déterminer les formes exponentielle et algébrique de $z_{2}$.
2. Soit $A$, $B$ et $C$ les points du plan d'affixes respectives : $z_{A} = 2 - 2i$, $z_{B} = - 2 - 2i$ et $z_{C} = - 4i$.
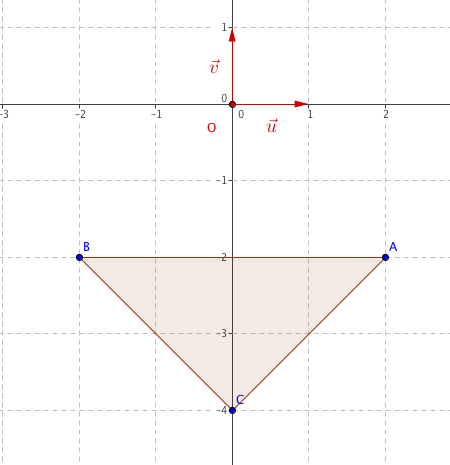
   1. Placer les points $A$, $B$ et $C$ dans le plan complexe.
   
   2. Calculer le produit scalaire $\vec{CA} \cdot \vec{CB}$.
      • Le vecteur $\vec{CA}$ a pour affixe $z_{\vec{CA}}=z_A-z_C=2-2i-(-4i)= 2-2i+4i= 2+2i$ donc $\vec{CA}$ a pour coordonnées $\begin{pmatrix} 2 \\ 2 \end{pmatrix}$
      • Le vecteur $\vec{CB}$ a pour affixe $z_{\vec{CB}}=z_B-z_C=2-2i-(-4i)= -2-2i+4i= -2+2i$ donc $\vec{CB}$ a pour coordonnées $\begin{pmatrix} -2 \\ 2 \end{pmatrix}$
      • $\vec{CA} \cdot \vec{CB} = XX'+YY' = 2 \times (-2) + 2\times 2 =-4 + 4 +0$
      $\vec{CA} \cdot \vec{CB} =0$, ce qui montre que les vecteurs $\vec{CA}$ et $ \vec{CB}$ sont orthogonaux et donc le triangle $ABC$ est rectangle en $C$.
   3. Déterminer la nature du triangle $ABC$.
   On sait déjà que $ABC$ est rectangle en $C$ ;
   $CA =\vert z_A-z_C\vert =\vert 2+2i \vert =\sqrt{2^2+2^2}= \sqrt 8 = 2\sqrt 2$
   $CB =\vert z_B-z_C\vert =\vert -2+2i \vert =\sqrt{2^2+2^2}= \sqrt 8 = 2\sqrt 2$
   Ayant $CA=CB$ , le triangle $ABC$ est rectangle isocèle en $C$.
   Le triangle $ABC$ est rectangle isocèle en $C$.