Lois normales - Table de $\pi(t)$

Page 3 sur 7: Table de $pi(t)$

La loi normale centrée réduite est caractérisée par la densité de probabilité~: $\displaystyle { f (x) = \dfrac{1}{\sqrt {2\pi }} e^{-x^2/2}. }$

 

Extraits de la table associée à la loi normale centrée réduite ${\cal N} (0, 1)$.

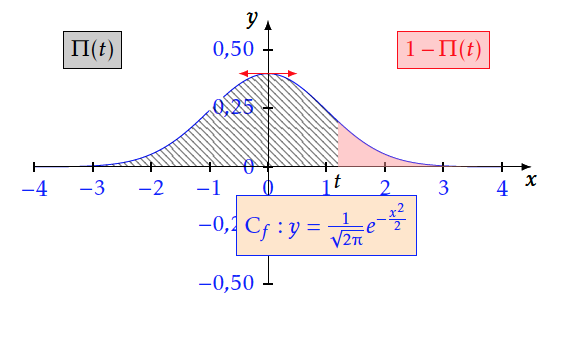
$$ \Pi (t) = P \big( T \leq t\big) = \int _{-\infty }^t f (x) \, {\rm d}x =0,5+\int _{0 }^t f (x) \, {\rm d}x \qquad \qquad $$ $f$ est continue sur $\mathbb{R}$, donc $\Pi'(t)=f(t)$.

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline & t&& 0,00&& 0,01&& 0,02&& 0,03&& 0,04&& 0,05&& 0,06&& 0,07&& 0,08&& 0,09 \\ \hline & 0,0&& 0,500\, 0&& 0,504\, 0&& 0,508\, 0&& 0,512\, 0&& 0,516\, 0&& 0,519\, 9&& 0,523\, 9&& 0,527\, 9&& 0,531\, 9&& 0,535\, 9 \\ \hline & 0,1&& 0,539\, 8&& 0,543\, 8&& 0,547\, 8&& 0,551\, 7&& 0,555\, 7&& 0,559\, 6&& 0,563\, 6&& 0,567\, 5&& 0,571\, 4&& 0,575\, 3 \\\hline & 0,2&& 0,579\, 3&& 0,583\, 2&& 0,587\, 1&& 0,591\, 0&& 0,594\, 8&& 0,598\, 7&& 0,602\, 6&& 0,606\, 4&& 0,610\, 3&& 0,614\, 1 \\\hline & 0,3&& 0,617\, 9&& 0,621\, 7&& 0,625\, 5&& 0,629\, 3&& 0,633\, 1&& 0,636\, 8&& 0,640\, 6&& 0,644\, 3&& 0,648\, 0&& 0,651\, 7 \\\hline & 0,4&& 0,655\, 4&& 0,659\, 1&& 0,662\, 8&& 0,666\, 4&& 0,670\, 0&& 0,673\, 6&& 0,677\, 2&& 0,680\, 8&& 0,684\, 4&& 0,687\, 9 \\\hline & 0,5&& 0,691\, 5&& 0,695\, 0&& 0,698\, 5&& 0,701\, 9&& 0,705\, 4&& 0,708\, 8&& 0,712\, 3&& 0,715\, 7&& 0,719\, 0&& 0,722\, 4 \\\hline & 0,6&& 0,725\, 7&& 0,729\, 1&& 0,732\, 4&& 0,735\, 7&& 0,738\, 9&& 0,742\, 2&& 0,745\, 4&& 0,748\, 6&& 0,751\, 7&& 0,754\, 9 \\\hline & 0,7&& 0,758\, 0&& 0,761\, 1&& 0,764\, 2&& 0,767\, 3&& 0,770\, 3&& 0,773\, 4&& 0,776\, 4&& 0,779\, 3&& 0,782\, 3&& 0,785\, 2 \\\hline & 0,8&& 0,788\, 1&& 0,791\, 0&& 0,793\, 9&& 0,796\, 7&& 0,799\, 5&& 0,802\, 3&& 0,805\, 1&& 0,807\, 8&& 0,810\, 6&& 0,813\, 3 \\\hline & 0,9&& 0,815\, 9&& 0,818\, 6&& 0,821\, 2&& 0,823\, 8&& 0,826\, 4&& 0,828\, 9&& 0,831\, 5&& 0,834\, 0&& 0,836\, 5&& 0,838\, 9 \\\hline & & & & & & & & & & & \\\hline & 1,0&& 0,841\, 3&& 0,843\, 8&& 0,846\, 1&& 0,848\, 5&& 0,850\, 8&& 0,853\, 1&& 0,855\, 4&& 0,857\, 7&& 0,859\, 9&& 0,862\, 1 \\\hline & 1,1&& 0,864\, 3&& 0,866\, 5&& 0,868\, 6&& 0,870\, 8&& 0,872\, 9&& 0,874\, 9&& 0,877\, 0&& 0,879\, 0&& 0,881\, 0&& 0,883\, 0 \\\hline & 1,2&& 0,884\, 9&& 0,886\, 9&& 0,888\, 8&& 0,890\, 6&& 0,892\, 5&& 0,894\, 3&& 0,896\, 2&& 0,898\, 0&& 0,899\, 7&& 0,901\, 5\\\hline & 1,3&& 0,903\, 2&& 0,904\, 9&& 0,906\, 6&& 0,908\, 2&& 0,909\, 9&& 0,911\, 5&& 0,913\, 1&& 0,914\, 7&& 0,916\, 2&& 0,917\, 7\\\hline & 1,4&& 0,919\, 2&& 0,920\, 7&& 0,922\, 2&& 0,923\, 6&& 0,925\, 1&& 0,926\, 5&& 0,927\, 9&& 0,929\, 2&& 0,930\, 6&& 0,931\, 9\\\hline & 1,5&& 0,933\, 2&& 0,934\, 5&& 0,935\, 7&& 0,937\, 0&& 0,938\, 2&& 0,939\, 4&& 0,940\, 6&& 0,941\, 8&& 0,942\, 9&& 0,944\, 1\\\hline & 1,6&& 0,945\, 2&& 0,946\, 3&& 0,947\, 4&& 0,948\, 4&& 0,949\, 5&& 0,950\, 5&& 0,951\, 5&& 0,952\, 5&& 0,953\, 5&& 0,954\, 5\\\hline & 1,7&& 0,955\, 4&& 0,956\, 4&& 0,957\, 3&& 0,958\, 2&& 0,959\, 1&& 0,959\, 9&& 0,960\, 8&& 0,961\, 6&& 0,962\, 5&& 0,963\, 3\\\hline & 1,8&& 0,964\, 1&& 0,964\, 9&& 0,965\, 6&& 0,966\, 4&& 0,967\, 1&& 0,967\, 8&& 0,968\, 6&& 0,969\, 3&& 0,969\, 9&& 0,970\, 6\\\hline & 1,9&& 0,971\, 3&& 0,971\, 9&& 0,972\, 6&& 0,973\, 2&& 0,973\, 8&& 0,974\, 4&& 0,975\, 0&& 0,975\, 6&& 0,976\, 1&& 0,976\, 7\\\hline & & & & & & & & & & &\\\hline & 2,0&& 0,977\, 2&& 0,977\, 8&& 0,978\, 3&& 0,978\, 8&& 0,979\, 3&& 0,979\, 8&& 0,980\, 3&& 0,980\, 8&& 0,981\, 2&& 0,981\, 7\\\hline & 2,1&& 0,982\, 1&& 0,982\, 6&& 0,983\, 0&& 0,983\, 4&& 0,983\, 8&& 0,984\, 2&& 0,984\, 6&& 0,985\, 0&& 0,985\, 4&& 0,985\, 7\\\hline & 2,2&& 0,986\, 1&& 0,986\, 4&& 0,986\, 8&& 0,987\, 1&& 0,987\, 5&& 0,987\, 8&& 0,988\, 1&& 0,988\, 4&& 0,988\, 7&& 0,989\, 0\\\hline & 2,3&& 0,989\, 3&& 0,989\, 6&& 0,989\, 8&& 0,990\, 1&& 0,990\, 4&& 0,990\, 6&& 0,990\, 9&& 0,991\, 1&& 0,991\, 3&& 0,991\, 6\\\hline & 2,4&& 0,991\, 8&& 0,992\, 0&& 0,992\, 2&& 0,992\, 5&& 0,992\, 7&& 0,992\, 9&& 0,993\, 1&& 0,993\, 2&& 0,993\, 4&& 0,993\, 6\\\hline & 2,5&& 0,993\, 8&& 0,994\, 0&& 0,994\, 1&& 0,994\, 3&& 0,994\, 5&& 0,994\, 6&& 0,994\, 8&& 0,994\, 9&& 0,995\, 1&& 0,995\, 2\\\hline & 2,6&& 0,995\, 3&& 0,995\, 5&& 0,995\, 6&& 0,995\, 7&& 0,995\, 9&& 0,996\, 0&& 0,996\, 1&& 0,996\, 2&& 0,996\, 3&& 0,996\, 4\\\hline & 2,7&& 0,996\, 5&& 0,996\, 6&& 0,996\, 7&& 0,996\, 8&& 0,996\, 9&& 0,997\, 0&& 0,997\, 1&& 0,997\, 2&& 0,997\, 3&& 0,997\, 4\\\hline & 2,8&& 0,997\, 4&& 0,997\, 5&& 0,997\, 6&& 0,997\, 7&& 0,997\, 7&& 0,997\, 8&& 0,997\, 9&& 0,997\, 9&& 0,998\, 0&& 0,998\, 1\\\hline & 2,9&& 0,998\, 1&& 0,998\, 2&& 0,998\, 2&& 0,998\, 3&& 0,998\, 4&& 0,998\, 4&& 0,998\, 5&& 0,998\, 5&& 0,998\, 6&& 0,998\, 6\\\hline \end{array} $$

Table pour les grandes valeurs de $ t$

$$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline & t && 3,0&& 3,1&& 3,2&& 3,3&& 3,4&& 3,5&& 3,6&& 3,8&& 4,0&& 4, 5 \\ \hline & \Pi (t)&& 0,998\, 65&& 0,999\, 04&& 0,999\, 31&& 0,999\, 52&& 0,999\, 66&& 0,999\, 76&& 0,999\, 841&& 0,999\, 928&& 0,999\, 968&& 0,999\, 997\\ \hline \end{array}$$

Nota :  La table donne les valeurs de $\Pi (t)$ pour $t$ positif.

Lorsque $t$ est négatif, il faut prendre le complément à l'unité de la valeur lue dans la table pour la valeur absolue de $t$.

Exemple :

 

pour $t=1,37$ ;$ \Pi (1,37)=0,914\, 7$

pour $t=-1,37$ ;$ \Pi (-1,37)=1-0,914\, 7=0,085\, 3$