Probabilités discrètes
ILes probabilités conditionnelles
AConditionnement
On définit la probabilité de $\displaystyle{B}$ sachant $\displaystyle{A}$ par :
$$ P_{A}(B) = \frac{P(A \cap B)}{P(A)} $$
BIndépendance
$$P(A \cap B) = P(A) \times P(B)$$
$$P(A \cap B) = P(A) \times P(B) \Leftrightarrow P_{A}(B) = P(B) \Leftrightarrow P_{B}(A) = P(A) $$
Soient $\displaystyle{X}$ et $\displaystyle{Y}$ deux variables aléatoires définies sur un univers $\displaystyle{\Omega}$ telles que :
- $\displaystyle{X(\Omega) = {x_{1}, x_{2},..., x_{n}}}$
- $\displaystyle{Y(\Omega) = {y_{1}, y_{2},..., y_{p}}}$
Les variables $\displaystyle{X}$ et $\displaystyle{Y}$ sont indépendantes si et seulement si, pour tout $\displaystyle{i}$ compris entre $\displaystyle{1}$ et $\displaystyle{n}$ et tout $\displaystyle{j}$ compris entre $\displaystyle{1}$ et $\displaystyle{p}$ :
$$P(X = x_{i} \cap Y = y_{j}) = P(X = x_{i}) \times P(Y = y_{j})$$
CLa formule des probabilités totales
Soit un ensemble $\displaystyle{E}$.
Les événements de probabilités non nulles $\displaystyle{\{E_{1}, E_{2}, E_{3},..., E_{k}\}}$ forment un système complet ou une partition de $\displaystyle{E}$ si et seulement si :
- $\displaystyle{\forall i \in [\![ 1 ; k ]\!] \text{ , } E_{i} \in E}$ ;
- les événements $\displaystyle{E_{1}, E_{2}, E_{3},..., E_{k}}$ sont deux à deux incompatibles ;
- et leur réunion est égale à l'ensemble $\displaystyle{E}$.
D'après la formule des probabilités totales, pour tout événement $\displaystyle{A}$ de E :
$$ P(A) = P(A \cap E_{1}) + P(A \cap E_{2}) + P(A \cap E_{3}) +... + P(A \cap E_{k}) $$
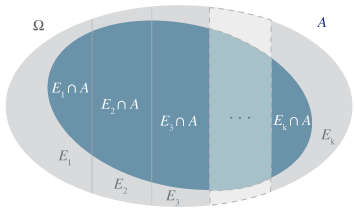
La formule des probabilités totales peut s'illustrer à l'aide d'un arbre pondéré :
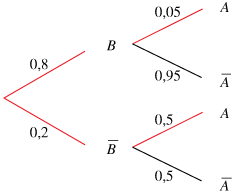
Dans cet exemple, $\displaystyle{\{B, \overline{B}\}}$ forme une partition de l'univers de l'expérience.
La formule des probabilités totales permet de calculer $\displaystyle{P(A)}$ :
$\displaystyle{P(A) = P(A \cap B) + P(A \cap \overline{B})}$
Soit : $\displaystyle{P(A) = P(B) \times P_{B}(A) + P(\overline{B}) \times P_{\overline{B}}(A)}$
La formule des probabilités totales revient ainsi à sommer les probabilités de tous les chemins de l'arbre menant à l'événement $\displaystyle{A}$ :
$\displaystyle{P(A) = 0,8 \times 0,05 + 0,2 \times 0,5}$
$\displaystyle{P(A) = 0,14}$
IILes lois de probabilité discrètes
ALes variables aléatoires
La loi de probabilité de $\displaystyle{X}$ associe à chaque réel $\displaystyle{x_{i}}$ la probabilité $\displaystyle{P(X = x_{i})}$.
On présente en général une loi de probabilité à l'aide d'un tableau.
| $\displaystyle{x_{i}}$ | $\displaystyle{x_{1}}$ | $\displaystyle{x_{2}}$ | ... | $\displaystyle{x_{n}}$ |
|---|---|---|---|---|
| $\displaystyle{P(X = x_{i})}$ | $\displaystyle{P(X = x_{1})}$ | $\displaystyle{P(X = x_{2})}$ | ... | $\displaystyle{P(X = x_{n})}$ |
$$E(X) = \sum_{i=0}^{n} x_{i} P(X = x_{i}) $$ Soit :
$$E(X) = x_{1} P(X = x_{1}) + x_{2} P(X = x_{2}) +... + x_{n} P(X = x_{n})$$
$$V(X) = \sum_{i=0}^{n} [x_{i} - E(X)]^{2} P(X = x_{i}) $$
$$σ(X) = \sqrt{ V(X) } $$
BLa loi de Bernoulli
Soit un réel $\displaystyle{p}$ compris entre $\displaystyle{0}$ et $\displaystyle{1}$.
Une épreuve de Bernoulli est une expérience aléatoire ne présentant que deux issues possibles :
- succès, de probabilité $\displaystyle{p}$
- échec, de probabilité $\displaystyle{1 - p}$.
Soit un réel $\displaystyle{p}$ compris entre $\displaystyle{0}$ et $\displaystyle{1}$.
Une variable aléatoire suit la loi de Bernoulli de paramètre $\displaystyle{p}$ si :
- $\displaystyle{X(\Omega) = \{0 ; 1\}}$
- $\displaystyle{P(X = 1) = p}$ et $\displaystyle{P(X = 0) = 1 - p}$
$$E(X) = p$$ $$V(X) = p(1 - p)$$
CLa loi binomiale
Soit un réel $\displaystyle{p}$ compris entre $\displaystyle{0}$ et $\displaystyle{1}$ et $\displaystyle{n}$ un entier naturel non nul.
Le nombre de succès dans la répétition de $\displaystyle{n}$ épreuves de Bernoulli identiques et indépendantes suit la loi binomiale de paramètres $\displaystyle{n}$ et $\displaystyle{p}$.
Une variable aléatoire suit ainsi la loi binomiale de paramètres $\displaystyle{n}$ et $\displaystyle{p}$, notée $\displaystyle{B(n ; p)}$, si :
- $\displaystyle{X(\Omega) = [\![0 ; n]\!]}$
- $\displaystyle{\forall k \in [\![0 ; n]\!] \text{ , } P(X = k) = \binom{n}{k} p^{k} (1 - p)^{n-k}}$
Le coefficient $\displaystyle{\binom{n}{k}}$ est égal au nombre de possibilités de placer les $\displaystyle{k}$ succès parmi les $\displaystyle{n}$ répétitions.
$$E(X) = np$$ $$V(X) = np(1 - p)$$
- Vues: 5524
