Nombres complexes
- I La notion de nombre complexe
- A L'ensemble des nombres complexes
- B La forme algébrique
- C Le conjugué et le module
- D La représentation analytique
- II Les équations dans $\displaystyle{\mathbb{C}}$
- A Résoudre une équation dans $\displaystyle{\mathbb{C}}$
- B Les équations du second degré
- III Les formes trigonométrique et exponentielle
- A La forme trigonométrique
- B La forme exponentielle
- C L'interprétation géométrique
ILa notion de nombre complexe
AL'ensemble des nombres complexes
On appelle $\displaystyle{i}$ le nombre (non réel) dont le carré est égal à $\displaystyle{- 1}$ :
$$ i^2 = -1 $$
$$ i^2 = -1 $$
Un nombre complexe est un nombre $\displaystyle{z}$ qui peut s'écrire sous la forme
$\displaystyle{z = x + iy}$ , avec $\displaystyle{x}$ et $\displaystyle{y}$ deux réels.
L'ensemble des nombres complexes est désigné par $\displaystyle{\mathbb{C}}$ .
L'ensemble des nombres complexes est désigné par $\displaystyle{\mathbb{C}}$ .
Les nombres suivants sont des complexes : $\displaystyle{4 - 2i}$, $\displaystyle{12}$, $\displaystyle{5i}$.
Les opérations dans $\displaystyle{\mathbb{C}}$ obéissent aux mêmes règles de calcul que dans $\displaystyle{\mathbb{R}}$.
BLa forme algébrique
L'écriture $\displaystyle{z = x + iy}$ est appelée forme algébrique de $\displaystyle{z}$. Elle est unique.
Soit un nombre complexe $\displaystyle{z = x + iy}$ :
- on appelle partie réelle de $\displaystyle{z}$, notée $\displaystyle{\text{Re}(z)}$, le réel $\displaystyle{x}$ ;
- on appelle partie imaginaire de $\displaystyle{z}$, notée $\displaystyle{\text{Im}(z)}$, le réel $\displaystyle{y}$.
Deux nombres complexes sont égaux si et seulement s'ils ont même partie réelle et même partie imaginaire.
- Le nombre $\displaystyle{z}$ est réel si et seulement si $\displaystyle{\text{Im}(z) = 0}$.
- Le nombre $\displaystyle{z}$ est imaginaire pur si et seulement si $\displaystyle{\text{Re}(z) = 0}$.
Soit $\displaystyle{z}$ un nombre complexe non nul, il existe un unique nombre complexe $\displaystyle{z'}$ tel que
$\displaystyle{zz' = 1}$.
Ce nombre est l'inverse de $\displaystyle{z}$, noté $\displaystyle{\frac{1}{z}}$.
Ce nombre est l'inverse de $\displaystyle{z}$, noté $\displaystyle{\frac{1}{z}}$.
CLe conjugué et le module
Soit un nombre complexe $\displaystyle{z = x + iy}$.
On appelle conjugué de $\displaystyle{z}$, noté $\displaystyle{\overline{z}}$, le complexe : $$x - iy$$
On appelle conjugué de $\displaystyle{z}$, noté $\displaystyle{\overline{z}}$, le complexe : $$x - iy$$
$\displaystyle{\overline{2 - 2i} = 2 + 2i}$
$\displaystyle{\overline{4i} = -4i}$
$\displaystyle{\overline{4i} = -4i}$
Soient $\displaystyle{z}$ et $\displaystyle{z'}$ deux nombres complexes.
- $\displaystyle{\overline{\overline{z}} = z}$
- $\displaystyle{z + \overline{z} = 2 \text{Re}(z)}$
- $\displaystyle{z - \overline{z} = 2i \text{ Im}(z)}$
- $\displaystyle{z}$ est réel $\displaystyle{\Leftrightarrow z = \overline{z}}$
- $\displaystyle{z}$ est imaginaire pur $\displaystyle{\Leftrightarrow z = - \overline{z}}$
- $\displaystyle{\overline{z + z'} = \overline{z} + \overline{z'}}$
- $\displaystyle{\overline{zz'} = \overline{z} \overline{z'}}$
- Si $\displaystyle{z'}$ non nul : $\displaystyle{\overline{ \left( \frac{z}{z’} \right) } = \frac{\overline{z}}{\overline{z'}}}$
- Pour tout entier $\displaystyle{n}$ : $\displaystyle{\overline{z^n} = (\overline{z})^{n}}$
Soit un nombre complexe $\displaystyle{z = x + iy}$.
On appelle module de $\displaystyle{z}$, noté $\displaystyle{|z|}$, le réel : $$\sqrt{ x^{2} + y^{2} }$$
On appelle module de $\displaystyle{z}$, noté $\displaystyle{|z|}$, le réel : $$\sqrt{ x^{2} + y^{2} }$$
$\displaystyle{|1 + 2i| = \sqrt{1^{2} + 2^{2}} = \sqrt{1 + 4} = \sqrt{5}}$
$\displaystyle{|-3i| = \sqrt{0^{2} + (-3)^{2}} = \sqrt{0 + 9} = \sqrt{9} = 3}$
$\displaystyle{|-3i| = \sqrt{0^{2} + (-3)^{2}} = \sqrt{0 + 9} = \sqrt{9} = 3}$
Soient $\displaystyle{z}$ et $\displaystyle{z’}$ deux nombres complexes.
- $\displaystyle{z \overline{z} = |z|^{2}}$
- $\displaystyle{|z| = |\overline{z}|}$
- $\displaystyle{|z| = |- z|}$
- $\displaystyle{|zz'| = |z| \times |z'|}$
- Si $\displaystyle{z'}$ non nul : $\displaystyle{\left| \frac{z}{z'} \right| = \frac{|z|}{|z'|}}$
- Pour tout entier $\displaystyle{n}$ : $\displaystyle{|z^{n}| = |z|^{n}}$
DLa représentation analytique
Soit un repère orthonormal direct du plan $\displaystyle{(O ; \overrightarrow{u} ; \overrightarrow{v} )}$.
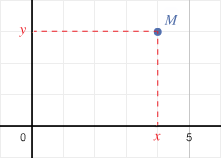
A tout point $\displaystyle{M}$ de coordonnées $\displaystyle{(x ; y)}$ on associe le nombre complexe $\displaystyle{z = x + iy}$ :
- le nombre complexe $\displaystyle{z}$ est appelé affixe du point $\displaystyle{M}$ (et du vecteur $\displaystyle{\overrightarrow{OM}}$) ;
- le point $\displaystyle{M}$ est appelé image du nombre complexe $\displaystyle{z}$.
On définit ainsi le plan complexe.
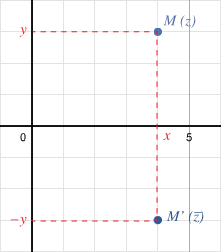
Les points $\displaystyle{M}$ et $\displaystyle{M'}$, images respectives des nombres complexes $\displaystyle{z}$ et $\displaystyle{\overline{z}}$ dans le plan complexe, sont symétriques par rapport à l'axe des abscisses.
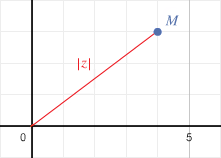
Le module $\displaystyle{|z|}$ du nombre complexe $\displaystyle{z}$, affixe du point $\displaystyle{M}$, est égal à la distance $\displaystyle{OM}$.
IILes équations dans $\displaystyle{\mathbb{C}}$
ARésoudre une équation dans $\displaystyle{\mathbb{C}}$
On résout une équation dans $\displaystyle{\mathbb{C}}$ à l'aide des mêmes techniques de calcul que dans $\displaystyle{\mathbb{R}}$.
BLes équations du second degré
Soit un trinôme du second degré à coefficients réels ($\displaystyle{a \neq 0}$) $\displaystyle{az^{2} + bz + c}$, avec $\displaystyle{\Delta \lt 0}$.
Ce trinôme admet deux racines complexes :
$$z_{1} = \frac{-b-i\sqrt{-\Delta}}{2a}$$ $$z_{2} = \frac{-b+i\sqrt{-\Delta}}{2a}$$
Ce trinôme admet deux racines complexes :
$$z_{1} = \frac{-b-i\sqrt{-\Delta}}{2a}$$ $$z_{2} = \frac{-b+i\sqrt{-\Delta}}{2a}$$
IIILes formes trigonométrique et exponentielle
ALa forme trigonométrique
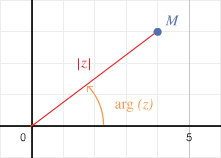
On appelle argument de $\displaystyle{z}$, noté $\displaystyle{\arg(z)}$ la mesure en radians de l'angle orienté
$\displaystyle{(\overrightarrow{u} ; \overrightarrow{OM})}$ :
$$\arg(z) = (\overrightarrow{u} ; \overrightarrow{OM}) [2\pi]$$
$$\arg(z) = (\overrightarrow{u} ; \overrightarrow{OM}) [2\pi]$$
Soit un nombre complexe $\displaystyle{z}$ non nul d'argument $\displaystyle{\theta}$. On peut alors exprimer $\displaystyle{z}$ sous sa forme trigonométrique :
$$z = |z| (\cos(\theta) + i\sin(\theta))$$
Réciproquement, si $\displaystyle{z = r (\cos(\theta) + i\sin(\theta))}$, avec $\displaystyle{r \gt 0}$ et $\displaystyle{\theta}$ réel quelconque, alors :
$$|z| = r$$ $$\arg(z) = \theta$$
$$z = |z| (\cos(\theta) + i\sin(\theta))$$
Réciproquement, si $\displaystyle{z = r (\cos(\theta) + i\sin(\theta))}$, avec $\displaystyle{r \gt 0}$ et $\displaystyle{\theta}$ réel quelconque, alors :
$$|z| = r$$ $$\arg(z) = \theta$$
Deux nombres complexes non nuls sont égaux si et seulement s'ils ont même module et même argument.
Soient $\displaystyle{z}$ et $\displaystyle{z'}$ deux nombres complexes non nuls.
- $\displaystyle{\arg(zz') = \arg(z) + \arg(z')}$
- $\displaystyle{\arg( \frac{1}{z} ) = - \arg(z)}$
- $\displaystyle{\arg( \frac{z}{z'} ) = \arg(z) - \arg(z')}$
- Pour tout entier naturel $\displaystyle{n}$ : $\displaystyle{\arg(z^{n}) = n \arg(z)}$
- $\displaystyle{z}$ est réel $\displaystyle{\Leftrightarrow \arg(z) = 0 [2\pi]}$ ou $\displaystyle{\arg(z) = \pi [2\pi]}$
- $\displaystyle{z}$ est imaginaire pur $\displaystyle{\Leftrightarrow \arg(z) = \frac{\pi}{2} [2\pi]}$ ou $\displaystyle{\arg(z) = - \frac{\pi}{2} [2\pi]}$
BLa forme exponentielle
Pour tout réel $\displaystyle{\theta}$, on pose :
$$e^{i\theta} = \cos(\theta) + i\sin(\theta)$$
$$e^{i\theta} = \cos(\theta) + i\sin(\theta)$$
Attention, une exponentielle complexe peut être négative, par exemple $\displaystyle{e^{i\pi} = -1}$.
Soit un nombre complexe $\displaystyle{z}$ non nul d'argument $\displaystyle{\theta}$. On peut alors exprimer $\displaystyle{z}$ sous sa forme exponentielle :
$$z = |z| e^{i\theta}$$
Réciproquement, si $\displaystyle{z = re^{i\theta}}$, avec $\displaystyle{r \gt 0}$ et $\displaystyle{\theta}$ réel quelconque, alors :
$$|z| = r$$ $$arg(z) = \theta$$
$$z = |z| e^{i\theta}$$
Réciproquement, si $\displaystyle{z = re^{i\theta}}$, avec $\displaystyle{r \gt 0}$ et $\displaystyle{\theta}$ réel quelconque, alors :
$$|z| = r$$ $$arg(z) = \theta$$
Soient $\displaystyle{\theta}$ et $\displaystyle{\theta'}$ deux réels.
- $\displaystyle{\overline{e^{i\theta}} = e^{-i\theta}}$
- $\displaystyle{e^{i(\theta+\theta')} = e^{i\theta} e^{i\theta'}}$
- $\displaystyle{\frac{1}{e^{i\theta}} = e^{-i\theta}}$
- Pour tout entier $\displaystyle{n}$ : $\displaystyle{(e^{i\theta})^{n} = e^{in\theta}}$
CL'interprétation géométrique
Soient $\displaystyle{A}$ et $\displaystyle{B}$ deux points d'affixes respectives $\displaystyle{z_{A}}$ et $\displaystyle{z_{B}}$ :
$$AB = |z_{B} - z_{A}|$$
$$AB = |z_{B} - z_{A}|$$
Soient $\displaystyle{A}$ et $\displaystyle{B}$ deux points d'affixes respectives $\displaystyle{z_{A}}$ et $\displaystyle{z_{B}}$ :
$$(\overrightarrow{u} ; \overrightarrow{AB}) = \arg(z_{B} - z_{A})$$
$$(\overrightarrow{u} ; \overrightarrow{AB}) = \arg(z_{B} - z_{A})$$
Soient $\displaystyle{\overrightarrow{v_{1}}}$ et $\displaystyle{\overrightarrow{v_{2}}}$ deux vecteurs non nuls d'affixes respectives $\displaystyle{z_{1}}$ et $\displaystyle{z_{2}}$ :
$$(\overrightarrow{v_{1}} ; \overrightarrow{v_{2}}) = \arg\left( \frac{z_{2}}{z_{1}} \right)$$
$$(\overrightarrow{v_{1}} ; \overrightarrow{v_{2}}) = \arg\left( \frac{z_{2}}{z_{1}} \right)$$
Soient $\displaystyle{A}$, $\displaystyle{B}$ et $\displaystyle{C}$ trois points distincts d'affixes respectives $\displaystyle{z_{A}}$, $\displaystyle{z_{B}}$ et $\displaystyle{z_{C}}$ :
$$(\overrightarrow{AB} ; \overrightarrow{AC}) = \arg\left( \frac{z_{C} - z_{A}}{z_{B} - z_{A}} \right)$$
$$(\overrightarrow{AB} ; \overrightarrow{AC}) = \arg\left( \frac{z_{C} - z_{A}}{z_{B} - z_{A}} \right)$$
- Vues: 5578
