Fonction logarithme népérien
ILes propriétés caractéristiques du logarithme népérien
ALa caractérisation
La fonction logarithme népérien, définie sur $\displaystyle{\mathbb{R}^{+*}}$ et notée $\displaystyle{\ln}$, est la bijection réciproque de la fonction exponentielle :
$$\forall x \gt 0 \text{ , } \ln(x) = y \Leftrightarrow x = e^{y}$$
$$\forall x \gt 0 \text{ , } \ln(x) = y \Leftrightarrow x = e^{y}$$
- Pour tous réels strictement positifs $\displaystyle{x}$ et $\displaystyle{y}$ : $\displaystyle{\ln(xy) = \ln(x) + \ln(y)}$
- Pour tout réel $\displaystyle{x}$ : $\displaystyle{\ln(e^{x}) = x}$
- Pour tout réel $\displaystyle{x}$ strictement positif : $\displaystyle{e^{\ln(x)} = x}$
- $\displaystyle{\ln(1) = 0}$
BLe signe

CLes propriétés algébriques
Pour tous réels strictement positifs $\displaystyle{x}$ et $\displaystyle{y}$, et tout entier naturel $\displaystyle{n}$ :
- $\displaystyle{\ln(xy) = \ln(x) + \ln(y)}$
- $\displaystyle{\ln \left( \frac{1}{x} \right) = - \ln(x)}$
- $\displaystyle{\ln \left( \frac{x}{y} \right) = \ln(x) - \ln(y)}$
- $\displaystyle{\ln(x^{n}) = n \ln(x)}$
- $\displaystyle{\ln( \sqrt{ x } ) = \frac{1}{2} \ln(x)}$
IIEtude du logarithme népérien
ALes limites
Les limites de la fonction logarithme népérien aux bornes de son ensemble de définition sont :
$$\lim_{x \to 0} \ln(x) = - \infty$$ $$\lim_{x \to +\infty} \ln(x) = + \infty$$
$$\lim_{x \to 0} \ln(x) = - \infty$$ $$\lim_{x \to +\infty} \ln(x) = + \infty$$
D'après le théorème des croissances comparées, pour tout entier naturel non nul $\displaystyle{n}$ :
$$ \lim_{x \to +\infty} \frac{\ln(x)}{x^n} = 0$$$$\lim_{x \to 0^{+}} x^n \ln(x) = 0$$
$$ \lim_{x \to +\infty} \frac{\ln(x)}{x^n} = 0$$$$\lim_{x \to 0^{+}} x^n \ln(x) = 0$$
Le nombre dérivé de la fonction logarithme népérien en $\displaystyle{1}$ étant égal à $\displaystyle{1}$ :
$$ \lim_{x \to 1} \frac{\ln(x)}{x-1} = 1$$
$$ \lim_{x \to 1} \frac{\ln(x)}{x-1} = 1$$
BLa dérivée
La fonction logarithme népérien est dérivable sur $\displaystyle{\mathbb{R}^{+*}}$.
Pour tout réel $\displaystyle{x}$ strictement positif :
$$\ln'(x) = \frac{1}{x} $$
Pour tout réel $\displaystyle{x}$ strictement positif :
$$\ln'(x) = \frac{1}{x} $$
Soit $\displaystyle{u}$ une fonction dérivable et strictement positive sur un intervalle $\displaystyle{I}$.
La composée $\displaystyle{\ln(u)}$ est alors dérivable sur $\displaystyle{I}$, et pour tout réel $\displaystyle{x}$ de $\displaystyle{I}$ :
$$(\ln(u))'(x) = \frac{u’(x)}{u(x)} $$
La composée $\displaystyle{\ln(u)}$ est alors dérivable sur $\displaystyle{I}$, et pour tout réel $\displaystyle{x}$ de $\displaystyle{I}$ :
$$(\ln(u))'(x) = \frac{u’(x)}{u(x)} $$
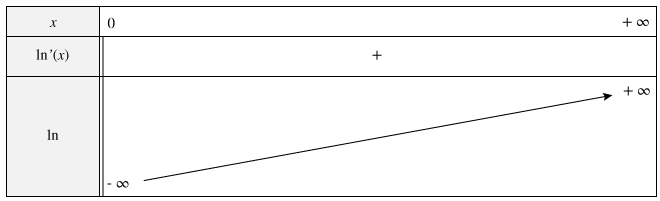
CLe sens de variation
La fonction logarithme népérien est strictement croissante sur $\displaystyle{\mathbb{R}^{+*}}$.
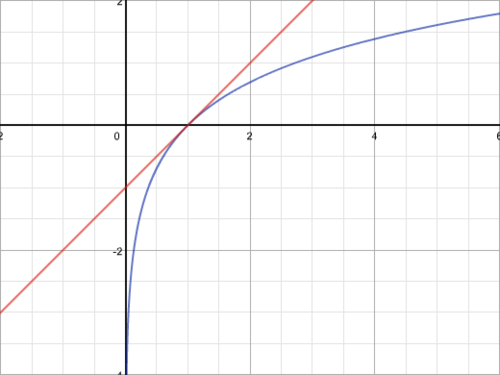
La droite d’équation $\displaystyle{y = x - 1}$ est tangente à la courbe représentative de la fonction logarithme népérien au point d’abscisse $\displaystyle{1}$ :
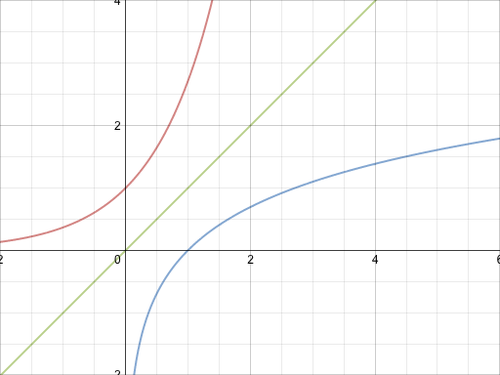
De plus, les fonctions exponentielle et logarithme népérien étant réciproques, leurs courbes représentatives sont symétriques par rapport à la droite d'équation $\displaystyle{y = x}$ :
DLe logarithme décimal
La fonction logarithme décimal, notée $\displaystyle{\log}$, est définie sur $\displaystyle{\mathbb{R}^{+*}}$ par :
$$\log(x) = \frac{\ln(x)}{\ln(10)} $$
$$\log(x) = \frac{\ln(x)}{\ln(10)} $$
- $\displaystyle{\log(10) = 1}$
- $\displaystyle{\log(10^n) = n}$, pour tout entier naturel $\displaystyle{n}$
- Vues: 7103
