Dérivées - Applications
Applications
Variations
- $f'(x)>0$ sur $[ a; b ]$ (sauf en des points isolés\footnotemark) $\iff$ $f$ strictement croissante sur $[ a; b ]$.
- $f'(x)<0$ sur $[ a; b ]$ (sauf en des points isolés) $\iff$ $f$ strictement décroissante sur $[ a; b ]$.
- $f'(x)=0$ sur $[ a; b ]$ si et seulement si $f$ constante sur $[ a; b ]$.
- si $f$ admet un maximum ou un minimum local en $x_0$, alors $f'(x_0)=0$.
- la réciproque est vrai seulement si $f$ change de signe en $x_0$.
Preuve (non rigoureuse, il s'agit seulement d'une idée) : Si $f'(x)>0$ sur $I$, cela signifie que toutes les tangentes à $\mathcal C_f$ sur $I$ ont des coefficients directeurs strictement positifs, donc sont strictement croissantes. Au voisinage de $x\in I$,
la courbe et sa tangente étant presque identiques, la fonction $f$ est également strictement croissante au voisinage de chaque $x\in I$, donc sur l'intervalle $I$ tout entier.
c'est-à-dire : on n'a pas $f'(x)=0$ sur un intervalle ouvert contenu dans $[a,b]$
Exemple
Dresser le tableau de variations de $g:\left]-\dfrac\pi2;\dfrac\pi2\right[\to\mathbb{R}, x\mapsto \tan(x)$
Lecture graphique
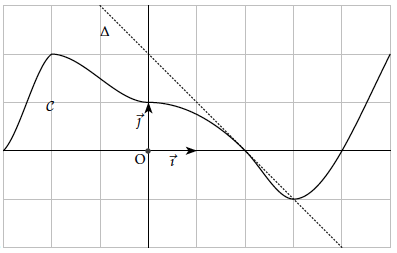
$\mathcal C$ représente $f:[-3;5]\to\mathbb{R}$, $\Delta$ est tangente à $\mathcal C$ en $(2;0)$.
Résoudre
- Calculer $f'(2)$.
- $f'(x)=0$
- Résoudre $f'(x)\leq 0$
Limites
Methode : Les limites de taux d'accroissement que l'on a calculé permettent, en les réutilisant, de lever certaines formes indéterminées : lorsqu'on reconnaît le taux d'accroissement d'une fonction $f$ dérivable en $x_0$, la limite en $0$ de cet taux est $f'(x_0)$. Exemple
$\displaystyle\lim_{h\to 0}\dfrac{\sin(h)}{h}=1$
Dérivées des fonctions usuelles
$$\begin{array}{|c|c|c|c|} \hline f(x) &f'(x) &\text{ Domaine de validité } &\text{ Condition } \\ \hline k & 0 &\mathbb R &k\in\mathbb R\\ \hline x & 1 &\mathbb R &\\ \hline ax+b &a & \mathbb{R} &a,b\in \mathbb{R} \\ \hline \displaystyle \frac 1 x &-\displaystyle \frac 1 {x^2} & \mathbb{R}-\{0\} & \\ \hline x^n & nx^{n-1} &\mathbb R:(n\geq 0); \mathbb{R}-\{0\}:(n<0) &n\in\mathbb{Z}-\{0\} \\ \hline \sqrt x & \displaystyle \frac 1 {2\sqrt x} &]0,+\infty[ &\\ \hline \cos(x) & -\sin(x) & \mathbb{R} & \\ \hline \sin(x) & \cos(x) & \mathbb{R} & \\ \hline \ln(x) &\displaystyle \frac 1 x &]0,+\infty[ & \\ \hline e^x &e^x &x\in\mathbb R &\\ \hline \end{array}$$
Opérations sur les dérivées
Soient $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ et $k$ un réel. Alors, $$ \begin{array}{|c|c|c|} \hline \text{ Fonction } f & \text{ Fonction dérivée } f' &\text{ Domaine de validité} \\ \hline u+v & u'+v' &I \\ \hline uv & u'v+v'u &I \\ \hline ku & ku'&I \\ \hline \displaystyle \frac u v & \displaystyle \frac {u'v-v'u}{v^2} & \text{ tout } x\in I \text{ tel que } v(x)\neq 0\\ \hline \hline \displaystyle \frac 1 u & \displaystyle \frac {-1}{u^2}\times u' & \text{ tout } x\in I \text{ tel que } u(x)\neq 0\\ \hline u^n & nu^{n-1}\times u' &I ; n\in\mathbb{N}-\{0\} \\ \hline \sqrt u & \displaystyle \frac 1 {2\sqrt u}\times u' &x\in I \text{ tels que } u(x)>0\\ \hline \cos(u) & -\sin(u)\times u' &I \\ \hline \sin(u) & \cos(u)\times u' &I \\ \hline {\ln}(u) & \displaystyle \frac {1}u\times u' &x\in I \text{ tels que } u(x)>0\\ \hline e^u & e^u\times u' &I \\ \hline \end{array}$$
- 1
- 2
- 3
- 4
- Toutes les pages
- Vues: 14438
