Dérivées
Nombre dérivé
Remarque En physique, on notera souvent $\displaystyle f'(x_0)=\dfrac{df}{dx}(x_0)$.
Exemple
Soit $f:\mathbb{R}\rightarrow\mathbb{R}, x\mapsto x^2$. Pour tout $x\in\mathbb{R}$ et $h\neq 0$, le taux d'accroissement de $f$ est \[\tau_{x,h}f=\dfrac{(x+h)^2-x^2}h=\dfrac{2xh+h^2}h=2x+h\text{ donc } \displaystyle\lim_{h\to 0}\tau_{x,h}=2x=f'(x)\] Exemple
Montrer que $f:[0;+\infty[\to\mathbb{R}, \sqrt{x}$ n'est pas dérivable en $0$.Exemple
Montrer que $g:[0;+\infty[\to\mathbb{R}, x\mapsto x\sqrt{x}$ est dérivable en $0$. Calculer $g'(0)$.
Propriété Soit $f$ une fonction définie sur un intervalle ouvert $I$ et $x\in I$. Il existe une fonction $r$ et deux réels $a$ et $b$ tels que $\displaystyle\lim_{h\to 0}r(h)=0$ et $f(x+h)=b+ha+hr(h)$ si et seulement si $f$ est dérivable en
$x_0$. On a alors $f(x_0)=b$ et $f'(x_0)=a$.
Preuve
Si une telle fonction $r(h)$ existe, on a $f(x_0)=b$ en faisant tendre $h$ vers $0$. Ainsi, $r(h)=\tau_{x_0,h}-a$. Comme la limite en $0$ de $r(h)$ est nulle, $f$ est dérivable en $x_0$ et $f'(x_0)=a$.
Réciproquement, si $f$ est dérivable en $x_0$, la fonction définie par $r(h)=\tau_{x_0,h}-f'(x_0)$ possède les deux propriétés attendues.
Exemple
Soit $v:x\mapsto x^n$. Développer $v(x+h)$ à l'aide du binôme de Newton. Écrire $v(x+h)$ sous la forme $v(x+h)=v(x)+hb+hr(h)$ et en déduire $v'(x)$.
Interprétations
Interprétation géométrique
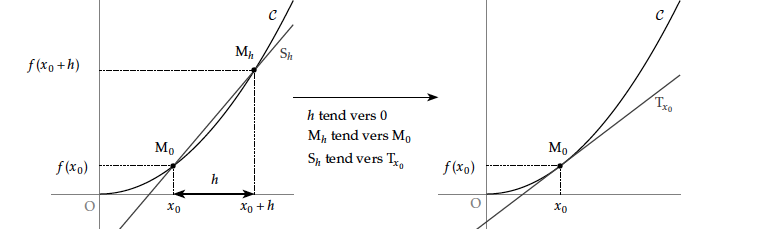
Soit $f$ une fonction définie sur $I$ et dérivable en $x_0\in I$. On note $\mathcal{ C}$ sa courbe représentative dans un repère orthonormé. On note $M_0$ le point de $\mathcal{ C}$ d'abscisse $x_0$ et $M_h$ le point de $\mathcal{ C}$d'abscisse $x_0+h$.
Le coefficient directeur de la sécante $S_h=(M_0M_h)$ à la courbe $\mathcal{ C}$ est le taux d'accroissement $\tau_{x_0,h}f$.
Lorsque $h$ tend vers $0$, la position limite de $M_h$ est celle du point $M$ et la position limite de la sécante $S_h$ est la tangente $T_{x_0}$ à $\mathcal C$ au point d'abscisse $x_0$.
Le coefficient directeur de cette tangente est $f'(x_0)$, la limite des coefficients directeurs des sécantes.
Soit $f$ une fonction définie sur $I$ et dérivable en $x_0\in I$. On note $\mathcal{ C}$ sa courbe représentative dans le plan muni d'un repère orthonormé $\left(\text{O},\vec{j},\vec{j},\vec{k}\right)$.
La tangente à la courbe $\mathcal C$ au point d'abscisse $x_0$ est la droite $T_{x_0}$ d'équation \[y=f'(x_0)(x-x_0)+f(x_0).\] En particulier, le coefficient directeur de cette tangente est le nombre $f'(x_0)$.
Exemple
Équation de la tangente à $\mathcal {P}:y=f(x)$ (où $f:x\mapsto x^2$) au point $A(1,1)$ ?
Remarque Si la limite en $x_0$ du taux d'accroissement $\tau_{x_0,h}f$ est $+\infty$ ou $-\infty$, la courbe $\mathcal C$ admet en $x_0$ une tangente verticale d'équation $x=x_0$.
Exemple
Montrer que la courbe de $x\mapsto\sqrt x$ admet une tangente verticale à l'origine. l
Interprétation cinétique
Soit $x(t)$ la position d'un mobile en mouvement rectiligne sur un axe gradué, en fonction du temps $t$. Le taux d'accroissement $\tau_{t_0,h}x$ représente la vitesse moyenne du mobile entre $t_0$ et $t_0+h$, alors que $x'(t)$ est la vitesse instantanée du mobile au temps $t$.
Interprétation numérique
Exemple
Soit $u:x\mapsto \dfrac 1x$. Donner $u'(1)$, une approximation de $\dfrac1{1+h}$ puis de $\dfrac{1}{1{,}001}$
Calcul de fonctions dérivées
En pratique, pour calculer les fonctions dérivées, on calcule une fois pour toute les dérivées de fonctions usuelles (par le taux d'accroissement, voir tableau onctionsusuelle ), et on les utilise avec les règles de calcul du tableau des dérivées et opérations :
Exemple
Soit $f:\mathbb{R}-\{0\}\to\mathbb{R}, x\mapsto \dfrac 1x$. Pour $x\neq 0$, calculer $\tau_{x,h}f$ et en déduire $f'(x)$.
Exemple
Soit $g:]0;+\infty[\to\mathbb{R}, x\mapsto \sqrt x$. Calculer $\tau_{x,h}f$ et en déduire $f'(x)$.
Opérations sur les dérivées
- $u+v$ est dérivable sur $I$ de dérivée $(u+v)'=u'+v'$.
- $uv$ est dérivable sur $I$ de dérivée $(uv)'=u'v+v'u$.
- $ku$ est dérivable sur $I$ de dérivée $(ku)'=ku'$. (où $k\in\mathbb {R}$)
- $\dfrac1v$ est dérivable sur $I$ privé des $x$ tels que $v(x)=0$, de dérivée $-\dfrac {v'}{v^2}$.
- $\dfrac uv$ est dérivable sur $I$ privé des $x$ tels que $v(x)=0$, de dérivée $\dfrac {u'v-v'u}{v^2}$.
Preuve
$\star$ Pour la somme, on calcule le taux d'accroissement de $(u+v)$ : $\tau_{x,h}(u+v)=\dfrac{u(x+h)+v(x+h)-(u(x)+v(x))}h=\dfrac{u(x+h)-u(x)}h+\dfrac{v(x+h)-v(x)}h=\tau_{x,h}u+\tau_{x,h}v$.
En faisant tendre $h$ vers $0$ on a bien : $(u+v)'(x)=u'(x)+v'(x)$.
$\star$ Pour le produit, on procède de même : $$\begin{array}\\ \tau_{x,h}(u\times v)(x)&=&\dfrac{u(x+h)\times v(x+h)-u(x)\times v(x)}h \\ &=& \dfrac{u(x+h)\times v(x+h)-u(x)v(x+h)+u(x)v(x+h)-u(x)\times v(x)}h \\ &=& \dfrac{u(x+h)-u(x)}h\times v(x+h)+u(x)\times\dfrac{v(x+h)-v(x)}h \end{array}$$
En faisant tendre $h$ vers $0$ on a bien : $(u\times v)'(x)= u'(x)v(x)+u(x)v'(x)$.
$\star$ La dérivée de $ku$ est un cas particulier de la situation précédente : $v(x)=k$ et $v'(x)=0$.
$\star$ La dérivée de $\dfrac 1v$ est un cas particulier de composition de fonctions.
$\star$ La dérivée de $\dfrac uv$ s'obtient par la formule de dérivée d'un produit appliquée à $u\times\dfrac 1v$.
Exemple
Dérivabilité et dérivée de $g:\mathbb{R}\to\mathbb{R}, x\mapsto x\sin(x)$
Exemple
Calculer la dérivée de $u:\mathbb{R}-\{0\}\to\mathbb{R}, x\mapsto \dfrac 1{x^n}$ ($n\geq 1$ entier). En déduire que la deuxième formule des dérivées usuelles est en fait valable pour $n\in \mathbb{Z}-\{0\}$.
Fonctions composées
Soit deux fonctions dérivables $u:I\to J$ et $v:J\to\mathbb{R}$. La fonction $v\circ u$ est dérivable de dérivée : $(v\circ u)'=u'\times(v'\circ u)$ (donc $(v\circ u)'(x)=u'(x)\times v'(u(x))$.
Preuve : On calcul le taux d'accroissement : pour $h$ tel que $v(u(x+h))-v(u(x))\neq 0$ : \[\tau_{x,h}v\circ u=\dfrac{v(u(x+h))-v(u(x))}{h}=\dfrac{v(u(x+h))-v(u(x))}{u(x+h)-u(x)}\times\dfrac {u(x+h)-u(x)}h\] Or $\displaystyle\lim_{x\to h}u(x+h)=u(x)$ donc par composition, en posant $X=u(x+h)$ et $X_0=u(x)$ : \[\displaystyle\lim_{h\to 0}\dfrac{v(u(x+h))-v(u(x))}{u(x+h)-u(x)}=\displaystyle\lim_{X\to X_0}\dfrac{v(X)-v(X_0)}{X-X_0}=v'(X_0)=v'(u(x))\] et par produit : $\displaystyle\lim_{h\to 0}\tau_{x,h}v\circ u=v'(u(x)) \times u'(x)$.
Exemple
Soit $u$ est dérivable sur $I$. Dérivabilité et dérivée de $u^n$ ?
Exemple
Soit $u$ est dérivable sur $I$. Dérivabilité et dérivée de $\sin(u)$ ?
Exemple
Soit $u$ est dérivable sur $I$ et strictement positive. Dérivabilité , dérivée de $\sqrt u$ ?
Exemple
Dérivabilité et dérivée de $f:]-\infty;3[, x\mapsto \sqrt{3-x}$.
Exemple
Dérivabilité et dérivée de $g:\mathbb{R}\rightarrow\mathbb{R}, x\mapsto \cos(x^2)$.
Applications
Variations
- $f'(x)>0$ sur $[ a; b ]$ (sauf en des points isolés\footnotemark) $\iff$ $f$ strictement croissante sur $[ a; b ]$.
- $f'(x)<0$ sur $[ a; b ]$ (sauf en des points isolés) $\iff$ $f$ strictement décroissante sur $[ a; b ]$.
- $f'(x)=0$ sur $[ a; b ]$ si et seulement si $f$ constante sur $[ a; b ]$.
- si $f$ admet un maximum ou un minimum local en $x_0$, alors $f'(x_0)=0$.
- la réciproque est vrai seulement si $f$ change de signe en $x_0$.
Preuve (non rigoureuse, il s'agit seulement d'une idée) : Si $f'(x)>0$ sur $I$, cela signifie que toutes les tangentes à $\mathcal C_f$ sur $I$ ont des coefficients directeurs strictement positifs, donc sont strictement croissantes. Au voisinage de $x\in I$,
la courbe et sa tangente étant presque identiques, la fonction $f$ est également strictement croissante au voisinage de chaque $x\in I$, donc sur l'intervalle $I$ tout entier.
c'est-à-dire : on n'a pas $f'(x)=0$ sur un intervalle ouvert contenu dans $[a,b]$
Exemple
Dresser le tableau de variations de $g:\left]-\dfrac\pi2;\dfrac\pi2\right[\to\mathbb{R}, x\mapsto \tan(x)$
Lecture graphique
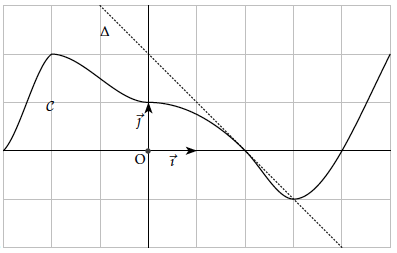
$\mathcal C$ représente $f:[-3;5]\to\mathbb{R}$, $\Delta$ est tangente à $\mathcal C$ en $(2;0)$.
Résoudre
- Calculer $f'(2)$.
- $f'(x)=0$
- Résoudre $f'(x)\leq 0$
Limites
Methode : Les limites de taux d'accroissement que l'on a calculé permettent, en les réutilisant, de lever certaines formes indéterminées : lorsqu'on reconnaît le taux d'accroissement d'une fonction $f$ dérivable en $x_0$, la limite en $0$ de cet taux est $f'(x_0)$. Exemple
$\displaystyle\lim_{h\to 0}\dfrac{\sin(h)}{h}=1$
Dérivées des fonctions usuelles
$$\begin{array}{|c|c|c|c|} \hline f(x) &f'(x) &\text{ Domaine de validité } &\text{ Condition } \\ \hline k & 0 &\mathbb R &k\in\mathbb R\\ \hline x & 1 &\mathbb R &\\ \hline ax+b &a & \mathbb{R} &a,b\in \mathbb{R} \\ \hline \displaystyle \frac 1 x &-\displaystyle \frac 1 {x^2} & \mathbb{R}-\{0\} & \\ \hline x^n & nx^{n-1} &\mathbb R:(n\geq 0); \mathbb{R}-\{0\}:(n<0) &n\in\mathbb{Z}-\{0\} \\ \hline \sqrt x & \displaystyle \frac 1 {2\sqrt x} &]0,+\infty[ &\\ \hline \cos(x) & -\sin(x) & \mathbb{R} & \\ \hline \sin(x) & \cos(x) & \mathbb{R} & \\ \hline \ln(x) &\displaystyle \frac 1 x &]0,+\infty[ & \\ \hline e^x &e^x &x\in\mathbb R &\\ \hline \end{array}$$
Opérations sur les dérivées
Soient $u$ et $v$ deux fonctions dérivables sur un intervalle $I$ et $k$ un réel. Alors, $$ \begin{array}{|c|c|c|} \hline \text{ Fonction } f & \text{ Fonction dérivée } f' &\text{ Domaine de validité} \\ \hline u+v & u'+v' &I \\ \hline uv & u'v+v'u &I \\ \hline ku & ku'&I \\ \hline \displaystyle \frac u v & \displaystyle \frac {u'v-v'u}{v^2} & \text{ tout } x\in I \text{ tel que } v(x)\neq 0\\ \hline \hline \displaystyle \frac 1 u & \displaystyle \frac {-1}{u^2}\times u' & \text{ tout } x\in I \text{ tel que } u(x)\neq 0\\ \hline u^n & nu^{n-1}\times u' &I ; n\in\mathbb{N}-\{0\} \\ \hline \sqrt u & \displaystyle \frac 1 {2\sqrt u}\times u' &x\in I \text{ tels que } u(x)>0\\ \hline \cos(u) & -\sin(u)\times u' &I \\ \hline \sin(u) & \cos(u)\times u' &I \\ \hline {\ln}(u) & \displaystyle \frac {1}u\times u' &x\in I \text{ tels que } u(x)>0\\ \hline e^u & e^u\times u' &I \\ \hline \end{array}$$
Des exercices pour s'entraîner
Exercice
Soit $f$ définie sur $[0;+\infty[$ par $f(x)=\sqrt{x}$.
- Étudier, en utilisant la définition, la dérivabilité de $f$ en $x_0= 3$.
- Étudier, en utilisant la définition, la dérivabilité de $f$ en $x_0 \in ]0;+\infty[$
- Que peut-on dire de la dérivabilité de $f$ en $0$ ?
Exercice
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=|x|$. On rappelle que $$f(x)= \left\{ \begin{array}{ll} x, & \text{ si } x\geq 0 ; \\ -x, & \text{ si } x< 0 . \end{array} \right.$$ Étudier la dérivabilité de $f$ en $x_0$ . (On pourra envisager plusieurs cas)
Exercice
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=|x^2-1|$.
Tracer sa représentation graphique en utilisant une calculatrice. Vérifier en utilisant les fonctions de zoom, que cette courbe présente deux points anguleux. Justifier en revenant à la définition du nombre dérivé.
Exercice
On considère les fonctions $f,g,h$ définies sur $\mathbb{R}$ par : $\displaystyle f(x)=k,k \in \mathbb{R};g(x)=x;c(x)=x^2$.
En utilisant la définition, démontrer que ces fonctions sont dérivables sur $\mathbb{R}$ et donner pour chacune d'elles sa fonction dérivée.
Exercice
Soit $n$ un entier naturel. On considère la fonction $x\mapsto x^n$.
(On conviendra que la fonction $x\mapsto x^0$ est la fonction constante $x \mapsto 1$)
Démontrer par récurrence que pour tout $n \geq 1,x \mapsto x^n$ est dérivable sur $\mathbb{R}$ et $(x^n)'=nx^{n-1}$ .
Démontrer que, pour tout $n \geq 1,x \mapsto x^{-n}$ est dérivable sur $]0;+\infty[$ et sur $]-\infty;0[ $ et $(x^{-n})'=-nx^{-n-1}$ .
Exercice
Calculer, en précisant l'intervalle considéré, les dérivées des fonctions suivantes : \[\begin{array}{l ll} \text{a.} : f(x)=x^3-3x^2+2x-5 .& \text{b.} : g(x)=\dfrac{x^2-3x+1}{5}. & \text{c.} : h(x)=2+\dfrac{1}{x}.\\ \text{d.} : p(x)=\dfrac{1}{2}x^4-x^3+\dfrac{5}{3}x.& \text{e.} : q(x)=\dfrac{3}{2x} .& \text{f.} : r(x)=\dfrac{x+1}{x-3}\\ \end{array}\]
Exercice
Calculer, en précisant l'intervalle considéré, les dérivées des fonctions suivantes : \[\begin{array}{l ll} \text{a.} : f(x)=\dfrac{\sin x}{x} .& \text{b.} : g(x)=\dfrac{1}{x^6}. & \text{c.} : h(x)=x\sqrt{x}.\\ \text{d.} : p(x)=(x-3)\dfrac{1}{x^2}.& \text{e.} : q(x)=\dfrac{x^2+x-1}{x^2+x+1} .& \text{f.} : r(x)=\dfrac{x+1}{\sqrt{x}}\\ \end{array}\]
Exercice
Calculer, en précisant l'intervalle considéré, les dérivées des fonctions suivantes : \[\begin{array}{l ll} \text{a.} : f(x)=\dfrac{\sin x}{\cos x} .& \text{b.} : g(x)=(x^3+3x)\sqrt{x}. & \text{c.} : h(x)=\dfrac{2+\cos x}{2+\sin x}.\\ \end{array}\]
Exercice
Soit $f$ la fonction définie par $\displaystyle\dfrac{x^2+1}{x-1}:$
La courbe représentative $\mathcal{C}$ de $f$ a-t-elle des tangentes parallèles à la droite $\Delta$ d'équation $y=-x+1 $ ? Si oui en quels points ?
Exercice
En utilisant la définition du nombre dérivé, déterminer : \[\begin{array}{l ll} \text{a.} : \displaystyle\lim_{x \to 3}\dfrac{\sqrt{x+6}-3}{x-3} .& \text{b.} : \displaystyle\lim_{x \to 0}\dfrac{\sin x}{x }. & \text{c.} : \displaystyle\lim_{x \to \dfrac{\pi}{2}}\dfrac{\cos x}{x-\dfrac{\pi}{2}}.\\ \end{array}\]
Exercice
On considère la fonction $f$ définie sur $]0;2[$ par $f(x)=\dfrac{1+x}{x^2-2x}$
- Donner les limites de $f$ aux bornes de son intervalle de définition.
- Justifier que $f$ est dérivable sur $]0;2[$ et calculer sa dérivée $f'$.
- Étudier le signe de $f'$ et donner le tableau de variations de $f$.
Exercice
$f$ est définie sur $\mathbb{R}$ par $f(x)=x^3-3x^2+1$
- Donner le tableau de variations de $f$.
- Représenter graphiquement $f$
- Quel est le nombre de solutions de l'équation $f(x)=0$. Donner une valeur approchée de chacune des solutions.
Exercice
$f$ est la fonction définie sur $[0;+\infty[$ par $f(x)=\dfrac{\sqrt{x}}{x^2+3}$
Donner le tableau de variations de $f$. Tracer la courbe représentative de $f$ , on étudiera en particulier la tangente à la courbe en son point d'abscisse $0$.
Exercice
Calculer les dérivées de : \[\begin{array}{l ll} \text{a.} : f(x)=\sin (x^2+1) .& \text{b.} : g(x)=\cos (\dfrac{1}{x}). & \text{c.} : h(x)=\dfrac{\sqrt{x+1}}{x-1}.\\ \end{array}\]
Exercice
Pour chacune des fonctions ci-dessous on considère un intervalle $I$ sur lequel la fonction est dérivable. Calculer alors la dérivée. \[\begin{array}{l lll} \text{a.} : r(x)=\sqrt {x^2+x} .& \text{b.} : s(x)=\sqrt {x^4+x^2}. & \text{c.} : p(x)=(x^2+x-5)^8.& \text{d.} : q(x)=\cos(x^4-x+2).\\ \end{array}\]
Exercice
Étudier la dérivabilité en $0$ des fonctions $r,s$ et $t$ : \[\begin{array}{l ll} \text{a.} : r(x)=\sqrt {x^2+x} .& \text{b.} : s(x)=\sqrt {x^4+x^2}. & \text{c.} : t(x)=\sqrt {x^4+x^6}.\\ \end{array}\]
Exercice
Le but de cet exercice est de calculer la limite suivante : $$\lim\limits_{h \to 0}\dfrac{(1+h)^{2007}-1}{h}$$ Pour cela, on considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = (1 + x)^{2007}$.
- Calculer la dérivée $f'$ de la fonction$f$.
- Calculer l'accroissement moyen de la fonction $f$ entre $0$ et $h$. En déduire la limite ci-dessus.
Exercice
On considère la fonction $f$ définie par : $f(x) =\sqrt{ x^2 - 4x}$
On note $C_f$ sa représentation graphique dans un repère orthonormal $(O, \vec{i},\vec{j} )$.
- Déterminer le domaine de définition $D_f$ de la fonction $f$.
- Étudier les limites de $f$ en 4 et en $+\infty$.
- Étude de la fonction $f$ sur $[4 ; +\infty[$:
- Étudier la dérivabilité de la fonction $f$ au point d'abscisse $x_0 = 4$.
- Calculer la dérivée $f'$ (pour $x > 4$). Établir le tableau de variations de $f$ sur l'intervalle $[4 ; +\infty[$.
- Tracer la courbe $C_f$ représentant $f$ sur l'intervalle $[4 ; 10]$.
Exercice
Soit $f$ la fonction numérique de la variable réelle $x$ définie sur $[0;1[$ par $f(x)=\dfrac{\sqrt{x^3}}{1-x }$ .
Partie A Tracé de la cissoïde de Dioclès
- Dresser le tableau des variations de $f$.
- Soit $\Gamma_1$ la courbe représentative de $f$ dans le plan rapporté à un repère orthonormal $\left(\text{O},\vec{j},\vec{j},\vec{k}\right)$. Déterminer une équation de la tangente $T$ à la courbe $\Gamma_1$ au point d'abscisse $\dfrac{1}{2}$ . Tracer la courbe $\Gamma_1$ et la droite $T$.
- Sur le même grahique, tracer la courbe $\Gamma_2$ image de $\Gamma_1$ par la réflexion d'axe $Ox$.
- Soit $\Gamma=\Gamma_1 \cup \Gamma_2$ . Montrer que $\Gamma$ a pour équation cartésienne $x^3+(x-1)y^2=0$ $\Gamma$ est appelée cissoïde de Dioclès.
Partie B Une propriété géométrique
- $I$ est le point de coordonnées $(1 ; 0)$ dans le repère $\left(\text{O},\vec{j},\vec{j},\vec{k}\right)$. $C$ est le cercle de diamètre $[OI]$ et $\Delta$ est la tangente à $C$ au point $I$. Soit $D$ la droite passant par $O$ et de coefficient directeur $(t,t \in \mathbb{R}$ .\\ Déterminer les coordonnées de $M$ , point d'intersection de $C$ et de $\Delta$, distinct de $O$. Déterminer les coordonnées de $N$ , point d'intersection de $\Delta$ et de $D$.
- Déterminer les coordonnées du point $M'$ tel que $\vec{OM'}=\vec{MN}$ .Montrer que $M'$ est un point de $\Gamma$.
Exercice
Soit $f$ la fonction définie sur l'intervalle [0 ; 1] par $f(x) = x - 2\sqrt{x} + 1$. Cette fonction est dérivable sur [0 ; 1] et sa dérivée $f'$ vérifie $f'(1) = 0$. La courbe représentative $\Gamma$ de la fonction $f$ dans un rep\`ere orthonormal est donnée ci-contre.\\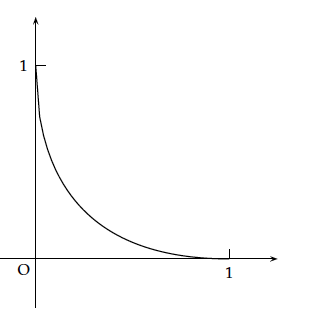
-
- Montrer que le point $M$ de coordonnées $(x, y)$ appartient à $\Gamma$ si et seulement si $x \geqslant 0, y \geqslant 0$ et $\sqrt{x} + \sqrt{y} = 1$.
- Montrer que $\Gamma$ est symétrique par rapport à la droite dont une équation est $y=x$.
-
- Si $\Gamma$ était un arc de cercle, quel serait son centre ? Quel serait son rayon ?
- La courbe $\Gamma$ est-elle un arc de cercle ?
Exercice
Une preuve de la divergence de certaines suites géométrique
- Montrez que, pour tout réel positif $x$ et tout entier naturel non nul $n$, on a $$(1+x)^n\geq 1+nx$$ déterminez le signe de $(1+x)^n-1-nx$ en étudiant une fonction.
- Que peut-on en déduire concernant les suites géométriques ?
Exercice
Étude d'une fonction irrationnelle avec problème de dérivabilité en un point. Étudiez et représentez graphiquement la fonction $$f : \ x\mapsto \dfrac{2}{5}\sqrt{25-x^2}$$ pour la dérivabilité en 5, utilisez la limite du taux d'accroissement.
Exercice
Étude d'une fonction trigonométrique. Étudiez et représentez graphiquement la fonction $$f : \ x\mapsto \tan x=\dfrac{\sin x}{\cos x}$$ commencez par régler les problèmes de définition, de périodicité et de parité.
Exercice
Résolution analytique d'un problème géométrique. Extremum d'une fonction. Un triangle $ABC$ isocèle, de sommet principal $A$, est inscrit dans un cercle de centre $O$ et de rayon 1. $H$ est le pied de la hauteur issue de $A$. On note $\alpha$ la mesure en radian de l'angle $\widehat{HOC}$. On suppose enfin que $0\leq\alpha\leq\dfrac{\pi}{2}$.
-
- Exprimez $BC$ et $AH$ en fonction de $\alpha$.
- En déduire, en fonction de $\alpha$, l'aire du triangle $ABC$.
- On considère la fonction $f$ définie sur $[0,\dfrac{\pi}{2}]$ par $$f(\alpha)=\sin\alpha(1+\cos\alpha)$$ Calculez la dérivée $f'$ de $f$ et prouvez que, pour tout réel $\alpha$ de $[0,\pi/2]$, on a $f'(\alpha)=2\cos^2\alpha+\cos\alpha-1$
-
- Factorisez le polynôme $2X^2+X-1$ et en déduire une factorisation de $f'(\alpha)$
- Dressez alors le tableau de variations de $f$.
- Démontrez qu'il existe une valeur de $\alpha$, que vous déterminerez, pour laquelle l'aire du triangle $ABC$ est maximale. Précisez ce maximum. Quelle est alors la nature du triangle $ABC$ ?
Exercice
Problème d'optimisation : les dents de la mer XXXII Albert est un fervent adepte de la plongée sous-marine. Alors qu'il se trouve en $A$ et s'émerveille devant la beauté du paysage aquatique,
il aperçoit au loin un requin d'une taille qui le dissuade de poursuivre plus avant son exploration des fonds marins et décide de rejoindre son bateau situé en $B$. À quel endroit doit-il rejoindre la surface pour que le temps de parcours soit minimal ?
Grâce à l'adrénaline secrétée par la portion médullaire de ses glandes surrénales, Albert se déplace à la vitesse de $7,2\,km.h^{-1}$ sous l'eau et à la vitesse de $9\,km.h^{-1}$ en surface. On supposera que la surface de l'eau est rectiligne,
que la dérive due au courant est nulle et que la trajectoire d'Albert est une ligne brisée.
Exercice
Une fonction avec valeur absolue Soit $f$ la fonction définie sur $\mathbb{R}$ par $$f(x)=\sqrt{|x^2+4x-5|}$$ Soit $C_f$ la courbe représentative de $f$ dans un repère orthogonal $\left(\text{O},~\vec{i},~\vec{i}\right)$.
- Écrivez $f(x)$ sans utiliser de valeur absolue.
- Montrez que $C_f$ admet la droite d'équation $x=-2$ comme axe de symétrie. Que peut-on en déduire sur le domaine d'étude de $f$.
- Étudiez les variations de $f$ là où elle est dérivable.
- Étudiez la dérivabilité de $f$ en 1. Interprétez graphiquement.
- Calculez $\displaystyle\lim_{x\rightarrow+\infty}\dfrac{f(x)}{x}$ puis $\displaystyle\lim_{x\rightarrow+\infty} f(x)-x$. Interprétez graphiquement.
- Tracez $C_f$. Vous prendrez 1cm comme unité en abscisse et 2cm en ordonnées. Vous prendrez soin de tracer les tangentes remarquables.
- Vues: 14440
