Baccalauréat S Centres étrangers 13 juin 2019 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
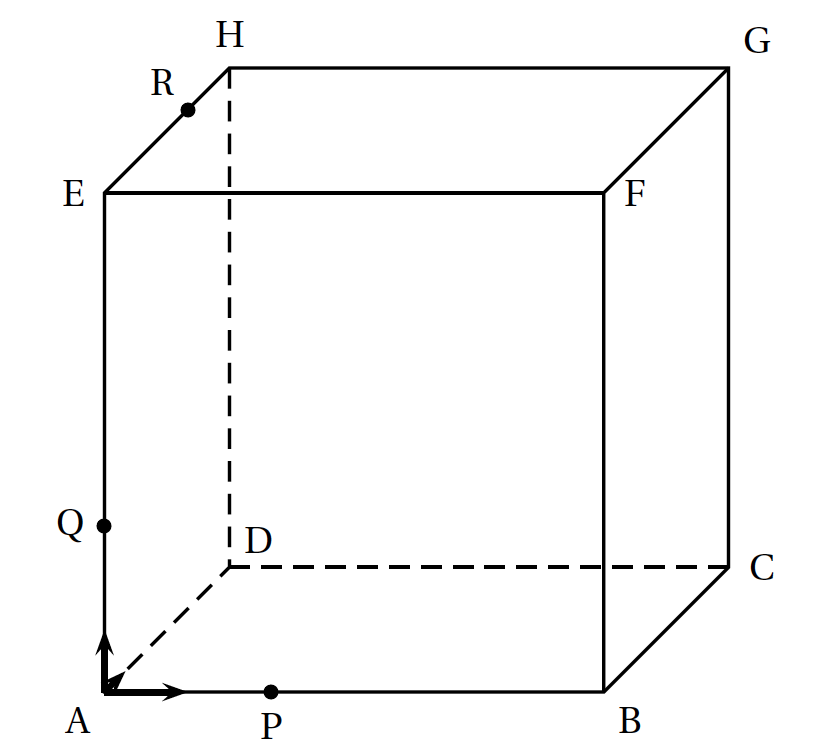
Dans l'espace, on considère un cube ABCDEFGH de centre $\Omega$ et d'arête de longueur $6$. Les points P, Q et R sont définis par : \[\vec{\text{AP}} = \dfrac{1}{3}\vec{\text{AB}},\: \vec{\text{AQ}} = \dfrac{1}{3}\vec{\text{AE}} \: \text{et}\: \vec{\text{HR}} = \dfrac{1}{3}\vec{\text{HE}}.\] Dans tout ce qui suit on utilise le repère orthonormé $\left(\text{A}~;~\vec{\imath},~\vec{\jmath},\vec{k}\right)$ avec : \[\vec{\imath} = \dfrac{1}{6}\vec{\text{AB}},\: \vec{\jmath} = \dfrac{1}{6}\vec{\text{AD}}\:\: \text{et}\:\: \vec{k} =\dfrac{1}{6}\vec{\text{AE}}.\] Dans ce repère, on a par exemple: \[\text{B}(6~;~0~;~0), \text{F}(6~;~0~;~6)\: \text{et }\:\: \text{R}(0~;~4~;~6).\]
-
- Donner, sans justifier, les coordonnées des points P, Q et $\Omega$. On a $P(2;0;0)$, $Q(0;0;2)$ et $\Omega(3;3;3)$
- $\quad$
- Déterminer les nombres réels $b$ et $c$ tels que $\vec{n}(1~;~b~;~c)$ soit un vecteur normal au plan (PQR) . On a $\vec{PQ}(-2;0;2)$, $R(0;4;6)$ et $\vec{PR}(-2;4;6)$.
- Si le vecteur $\vec{n}$ est normal au plan $(PQR)$ on a alors :
- $\vec{n}.\vec{PQ}=0 \iff -2+0+2c=0 \iff c=1$ et
- $\vec{n}.\vec{PR}=0 \iff -2+4b+6c=0 \iff -2+4b+6=0\iff b=-1$.
- $\quad$
- En déduire qu'une équation du plan (PQR) est : $x - y+ z - 2 = 0$. Le vecteur $\vec{n}(1;-1;1)$ est normal au plan $(PQR)$. Une équation cartésienne de ce plan est alors de la forme $x-y+z+d=0$
- Conclusion : Le vecteur $\vec{n}(1;-1;1)$ est normal au plan $(PQR)$.
- Le point $P(2;0;0)$ appartient au plan.
- Donc $2-0+0+d=0 \iff d=-2$
- Une équation cartésienne du plan $(PQR)$ est donc $x-y+z-2=0$.
- $\quad$
-
- On note $\Delta$ la droite perpendiculaire au plan (PQR) passant par le point $\Omega$, centre du cube. Donner une représentation paramétrique de la droite $\Delta$. Le vecteur $\vec{n}$ est un vecteur directeur de la droite $\Delta$.
- Une représentation paramétrique de cette droite est donc $$\begin{cases} x=t+3\\y=-t+3\\z=t+3\end{cases} \quad, t\in\mathbb R$$
- $\quad$
- En déduire que la droite $\Delta$ coupe le plan (PQR) au point I de coordonnées $\left(\dfrac{8}{3}~;~\dfrac{10}{3}~;~\dfrac{8}{3}\right)$. Par définition, le plan $(PQR)$ et la droite $\Delta$ sont sécants. Montrons que le point $I\left(\dfrac{8}{3};\dfrac{10}{3};\dfrac{8}{3}\right)$ appartient à la fois à la droite et au plan.
- Si $t=-\dfrac{1}{3}$ alors : $\begin{cases} x=-\dfrac{1}{3}+3=\dfrac{8}{3}\\y=\dfrac{1}{3}+3=\dfrac{10}{3}\\z=-\dfrac{1}{3}+3=\dfrac{8}{3}\end{cases}$.
- Donc $I\in \Delta$
- $\quad$
- $\begin{align*} &\dfrac{8}{3}-\dfrac{10}{3}+\dfrac{8}{3}-2\\
- &=\dfrac{6}{3}-2 \\
- &=0\end{align*}$
- Le point $I$ appartient également au plan $(PQR)$.
- Par conséquent, le point d’intersection de la droite $\Delta$ et du plan $(PQR)$ est $I\left(\dfrac{8}{3};\dfrac{10}{3};\dfrac{8}{3}\right)$.
- Calculer la distance $\OmegaI$ $\Omega I^2=\left(\dfrac{8}{3}-3\right)^2+\left(\dfrac{10}{3}-3\right)^2+\left(\dfrac{8}{3}-3\right)^2=\dfrac{1}{3}$
- Par conséquent $\Omega I=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$.
- $\quad$
- On considère les points J$(6~;~4~;~0)$ et K$(6~;~6~;~2)$.
- Justifier que le point J appartient au plan (PQR). $x_J - y_J+ z_J - 2=6-4+0-2=6-6=0$ donc $J\in (PQR)$.
- $\quad$
- Vérifier que les droites (JK) et (QR) sont parallèles. On a$\vec{JK}(0;2;2)$ et $\vec{QR}(0;4;4)$
- Ainsi $\vec{QR}=2\vec{JK}$
- Ces deux vecteurs sont colinéaires. Les droites $(JK)$ et $(QR)$ sont donc parallèles.
- $\quad$
- Sur la figure donnée en annexe, tracer la section du cube par le plan (PQR). On laissera apparents les traits de construction, ou bien on expliquera la démarche.
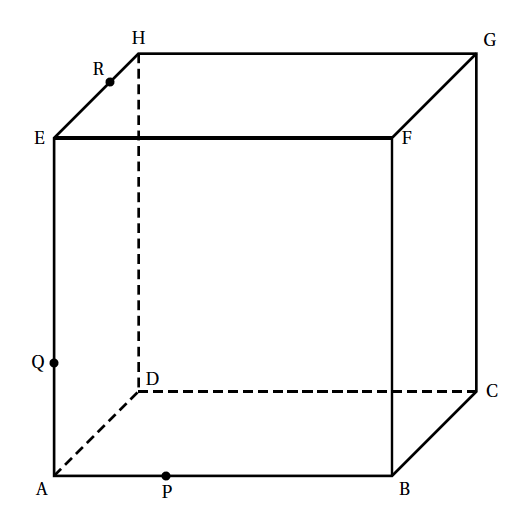 On place le point $J(6;4;0)$ (on reporte la distance $HR$ à partir de $C$).
On place le point $J(6;4;0)$ (on reporte la distance $HR$ à partir de $C$).
- On trace la parallèle à la droite $(QR)$ passant par $J$. Elle coupe la droite $(GC)$ en $K$.
- On trace la parallèle à la droite $(PJ)$ passant par $R$. Elle coupe la droite $(HG)$ en $S$.
- Pour terminer une figure interactive avec GeoGebra :
- Vues: 65559
