Baccalauréat S Centres étrangers 13 juin 2019 - Exercice 3
Page 5 sur 10
Exercice 3 5 points
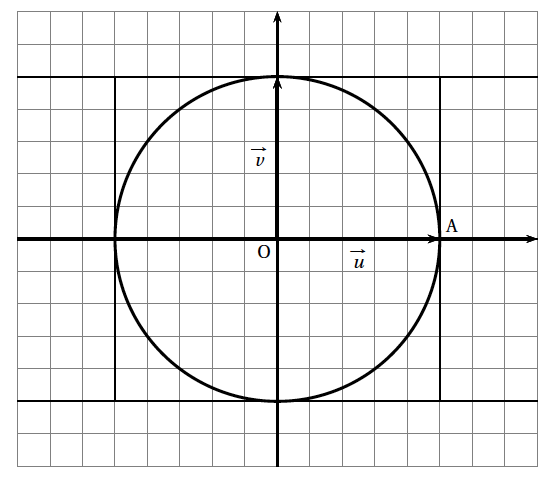
Le plan est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Le but de cet exercice est de déterminer les nombres complexes $z$ non nuls tels que les points d'affixes 1, $z^2$ et $\dfrac{1}{z}$ soient alignés. Sur le graphique fourni en annexe, le point A a pour affixe 1.
Partie A: étude d'exemples
- Un premier exemple
Dans cette question, on pose $z = \text{i}$.- Donner la forme algébrique des nombres complexes $z^2$ et $\dfrac{1}{z}$.
- Placer les points $N_1$ d'affixe $z^2$, et $P_1$ d'affixe $\dfrac{1}{z}$ sur le graphique donné en annexe. On remarque que dans ce cas les points A, $N_1$ et $P_1$ ne sont pas alignés.
- Une équation
Résoudre dans l'ensemble des nombres complexes l'équation d’inconnue $z$ : $z^2 + z + 1 = 0$. - Un deuxième exemple
Dans cette question, on pose : $z = - \dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$.- Déterminer la forme exponentielle de $z$, puis celles des nombres complexes $z^2$ et $\dfrac{1}{z}$.
- Placer les points $N_2$ d'affixe $z^2$ et $P_2$, d’affixe $\dfrac{1}{z}$ sur le graphique donné en annexe. On remarque que dans, ce cas les points A, $N_2$ et $P_2$ sont alignés.
Partie B
Soit $z$ un nombre complexe non nul. On note $N$ le point d’affixe $z^2$ et $P$ le point d’affixe $\dfrac{1}{z}$.
- Établir que, pour tout nombre complexe différent de $0$, on a : \[z^2 - \dfrac{1}{z} = \left(z^2 + z + 1 \right)\left(1 - \dfrac{1}{z} \right).\]
- On rappelle que si, $\vec{U}$ est un vecteur non nul et $\vec{V}$ un vecteur d’affixes respectives $z_{\vec{U}}$ et $z_{\vec{V}}$, les vecteurs $\vec{U}$ et $\vec{V}$ sont colinéaires si et seulement si il existe un nombre réel $k$ tel que $z_{\vec{V}} = k z_{\vec{U}}$. En déduire que, pour $z \ne 0$, les points A, $N$ et $P$ définis ci-dessus sont alignés si et seulement si $z^2 + z + 1$ est un réel.
- On pose $z = x+ \text{i}y$, où $x$ et $y$ désignent des nombres réels. Justifier que : $z^2 + z + 1 = x^2 - y^2 + x + 1 + \text{i} (2xy + y)$.
-
- Déterminer l'ensemble des points $M$ d'affixe $z \ne 0$ tels que les points A, $N$ et $P$ soient alignés.
- Tracer cet ensemble de points sur le graphique donné en annexe.
- Vues: 65559
