Baccalauréat S Métropole 22 juin 2018
Page 1 sur 10
Exercice 1 6 points
Dans cet exercice, on munit le plan d'un repère orthonormé.
On a représenté ci-dessous la courbe d'équation: \[y = \dfrac{1}{2}\left(\text{e}^x + \text{e}^{-x} - 2\right).\] Cette courbe est appelée une « chaînette ». On s'intéresse ici aux « arcs de chaînette» délimités par deux points de cette courbe symétriques par rapport à l'axe des ordonnées. Un tel arc est représenté sur le graphique ci-dessous en trait plein. On définit la « largeur » et la « hauteur » de l'arc de chaînette délimité par les points $M$ et $M'$ comme indiqué sur le graphique. 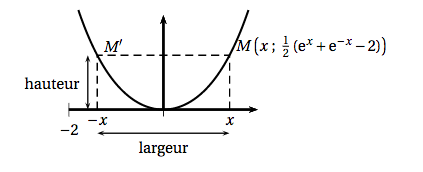
Le but de l'exercice est d'étudier les positions possibles sur la courbe du point $M$ d'abscisse $x$ strictement positive afin que la largeur de l'arc de chaînette soit égale à sa hauteur.
- Justifier que le problème étudié se ramène à la recherche des solutions strictement positives de l'équation \[(E) : \text{e}^x + \text{e}^{- x} - 2 = 0.\]
- On note $f$ la fonction définie sur l'intervalle $[0~;~ +\infty[$ par : \[f(x) = \text{e}^x + \text{e}^{- x} - 4x - 2.\]
- Vérifier que pour tout $x > 0,\: f(x) = x \left(\dfrac{\text{e}^x}{x}- 4\right) + \text{e}^{- x} - 2$.
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$.
-
- On note $f'$ la fonction dérivée de la fonction $f$. Calculer $f'(x)$, où $x$ appartient à l'intervalle $[0~;~ +\infty[$.
- Montrer que l'équation $f'(x) = 0$ équivaut à l'équation : $\left(\text{e}^x\right)^2 - 4\text{e}^x - 1 = 0$.
- En posant $X = \text{e}^x$, montrer que l'équation $f'(x) = 0$ admet pour unique solution réelle le nombre $\ln \left(2 + \sqrt{5}\right)$.
- On donne ci-dessous le tableau de signes de la fonction dérivée $f'$ de $f$ :
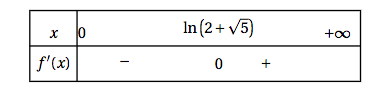
- Dresser le tableau de variations de la fonction $f$.
- Démontrer que l'équation $f(x) = 0$ admet une unique solution strictement positive que l'on notera $\alpha$.
- On considère l'algorithme suivant où les variables $a$, $b$ et $m$ sont des nombres réels : $$\begin{array}{|l|}\hline \text{Tant que } b - a > 0,1 \text{faire:}\\ \hspace{1cm} m \gets \dfrac{a+b}{2} \\ \hspace{1cm}\text{ Si } \text{e}^m + \text{e}^{-m} - 4m - 2 > 0 \text{, alors:}\\ \hspace{2cm} b \gets m \\ \hspace{1cm}\text{Sinon :}\\ \hspace{2cm} a\gets m \\ \hspace{1cm}\text{Fin Si }\\ \text{Fin Tant que }\\ \hline \end{array}$$
- Avant l'exécution de cet algorithme, les variables $a$ et $b$ contiennent respectivement les valeurs $2$ et $3$. Que contiennent-elles à la fin de l'exécution de l'algorithme ? On justifiera la réponse en reproduisant et en complétant le tableau ci-contre avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme.
- Comment peut-on utiliser les valeurs obtenues en fin d'algorithme à la question précédente ?
- La Gateway Arch, édifiée dans la ville de Saint-Louis aux États-Unis, a l'allure ci-contre. Son profil peut être approché par un arc de chaînette renversé dont la largeur est égale à la hauteur.
La largeur de cet arc, exprimée en mètre, est égale au double de la solution strictement positive de l'équation : \[\left(E'\right) : \text{e}^{\frac{t}{39}} + \text{e}^{-\frac{t}{39}} - 4\frac{t}{39} - 2 = 0.\] Donner un encadrement de la hauteur de la Gateway Arch.
- Vues: 52538
