Baccalauréat S Nouvelle-Calédonie Wallis et Futuna 28 novembre 2017 - Exercice 2

Page 3 sur 12: Exercice 2

Exercice 2 (5 points)

Commun à tous les candidats

On considère la fonction $f$ définie sur $]0~;~+\infty[$ par $$f(x)=\dfrac{\big(\ln x\big)^2}x.$$ On note $\mathcal C$ la courbe représentative de $f$ dans un repère orthonormé.

1. Déterminer la limite en $0$ de la fonction $f$ et interpréter graphiquement le résultat.
2. 1. Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f(x)=4\left(\dfrac{\ln\big(\sqrt x\big)}{\sqrt x}\right)^2.\]
   2. En déduire que l'axe des abscisses est une asymptote à la courbe représentative de la fonction $f$ au voisinage de $+ \infty$.
3. On admet que $f$ est dérivable sur $]0~;~+\infty[$ et on note $f'$ sa fonction dérivée.
   1. Démontrer que, pour tout $x$ appartenant à $]0~;~+\infty[$, \[f'(x)=\dfrac{\ln(x)\big(2-\ln(x)\big)}{x^2}.\]
   2. Étudier le signe de $f'(x)$ selon les valeurs du nombre réel $x$ strictement positif.
   3. Calculer $f(1)$ et $f\big(\text{e}^2\big)$.
   On obtient alors le tableau de variations ci-dessous.
   
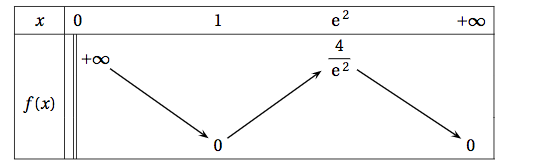
4. Démontrer que l'équation $f(x) = 1$ admet une unique solution $\alpha$ sur $]0~;~+\infty[$ et donner un encadrement de $\alpha$ d'amplitude $10^{-2}$.