Baccalauréat S Liban 27 mai 2014 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Fonctions

Soit $f$ la fonction définie sur l'intervalle $[0~;~+\infty[$ par \[f(x) = x\,\mathrm{e}^{-x}.\] On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthogonal.

Partie A

1. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle $[0;~+\infty[$. Pour tout réel $x$ de l'intervalle $[0~;~+\infty[$, calculer $f'(x)$. En déduire les variations de la fonction $f$ sur l'intervalle $[0~;~+\infty[$.
$f'(x)=\mathrm{e}^{-x}-x\mathrm{e}^{-x}=(1 - x)\mathrm{e}^{-x}$ $\mathrm{e}^{-x}$ étant toujours strictement positif, $f'(x)$ sera du signe de $1-x$. Il s'ensuit que \[f'(x)\geqslant0\quad \text{ sur }\quad [0,~1]\quad \text{ et }\quad f'(x)<0\quad \text{ sur }\quad ]1,~+\infty[\] $f$ est donc croissante sur $[0,~1]$ et décroissante sur $]1,~+\infty[$.
2. Déterminer la limite de la fonction $f$ en $+\infty$. Quelle interprétation graphique peut-on faire de ce résultat?
On sait que $\lim\limits_{x\rightarrow +\infty} x\,\mathrm{e}^{-x}=0$, ce qui signifie que l'axe des abscisses est une asymptote horizontale à la courbe $\mathcal{C}$

Partie B

Soit $\mathcal{A}$ la fonction définie sur l'intervalle $[0;~+\infty[$ de la façon suivante :
pour tout réel $t$ de l'intervalle $[0~;~+\infty[\,,\,\mathcal{A}(t)$ est l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe $\mathcal{C}$ et les droites d'équations $x = 0$ et $x = t$.

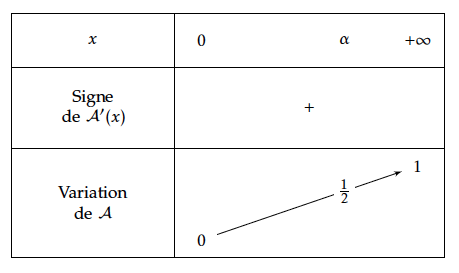
1. Déterminer le sens de variation de la fonction $\mathcal{A}$.
Comme la fonction $f$ est continue et positive sur l'intervalle $[0;~+\infty[$ alors \[\mathcal{A}(t)=\int_0^t f(x)\,\mathrm{d}x\]et donc, pour tout $t\in [0;~+\infty[\quad \mathcal{A}'(t)=f(t)$ Comme $f$ est positive sur l'intervalle $[0~;~+\infty[$ il s'ensuit que la fonction $\mathcal{A}$ est croissante sur $[0~;~+\infty[$.
2. On admet que l'aire du domaine délimité par la courbe $\mathcal{C}$ et l'axe des abscisses est égale à 1 unité d'aire. Que peut-on en déduire pour la fonction $\mathcal{A}$?
On peut en déduire que la fonction $\mathcal{A}$ a pour limite 1 en $+\infty$.
3. On cherche à prouver l'existence d'un nombre réel $\alpha$ tel que la droite d'équation $x =\alpha$ partage le domaine compris entre l'axe des abscisses et la courbe $\mathcal{C}$, en deux parties de même aire, et à trouver une valeur approchée de ce réel.
   1. Démontrer que l'équation $\mathcal{A}(t)=\dfrac12$ admet une unique solution sur l'intervalle $[0~;~+\infty[$
   Dressons le tableau de variations de la fonction $\mathcal{A}$ sur $[0~;~+\infty[$ :
   
   
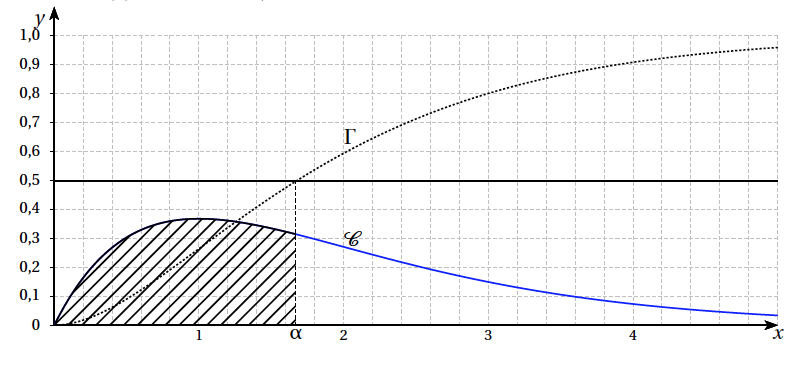
   1. Sur le graphique fourni en annexe à rendre avec la copie sont tracées la courbe $\mathcal{C}$, ainsi que la courbe $\Gamma$ représentant la fonction $\mathcal{A}$.
      Sur le graphique de l' annexe, identifier les courbes $\mathcal{C}$ et $\Gamma$, puis tracer la droite d'équation $y=\dfrac12$. En déduire une valeur approchée du réel $\alpha$.
   
   
   Hachurer le domaine correspondant à $\mathcal{A}(\alpha)$.

• On définit la fonction $g$ sur l'intervalle $[0;~+\infty[$ par $g(x) = (x+1)\,\mathrm{e}^{-x}$.
  1. On note $g'$ la fonction dérivée de la fonction $g$ sur l'intervalle $[0;~+\infty[$.
  Pour tout réel $x$ de l'intervalle $[0;~+\infty[$, calculer $g'(x)$.

$g'(x)= \mathrm{e}^{-x}-(x+1)\mathrm{e}^{-x}=-x\,\mathrm{e}^{-x}$

• En déduire, pour tout réel $t$ de l'intervalle $[0;~+\infty[$, une expression de $\mathcal{A}(t)$.

On remarque que $g'(x)= -f(x)$, d'où \[\mathcal{A}(t)=\int_0^t f(x)\,\mathrm{d}x =\int_0^t -g'(x)\,\mathrm{d}x=\left[-g(x)\right]_0^t = -g(t)+g(0)=1-(1+t)\mathrm{e}^{-t}\]

• Calculer une valeur approchée à $10^{-2}$ près de $\mathcal{A}(6)$.

$\mathcal{A}(6)=1-7\mathrm{e}^{-6}\simeq 0,98$