Baccalauréat S Polynésie 14 juin 2017 - Exercice 2

Exercice 2 5 points

Commun à tous les candidats

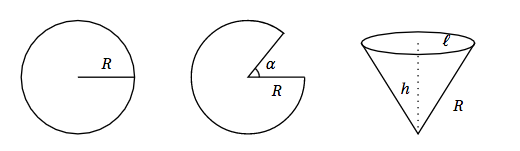
Dans un disque en carton de rayon $R$ , on découpe un secteur angulaire correspondant à un angle de mesure $\alpha$ radians. On superpose les bords afin de créer un cône de révolution. On souhaite choisir l'angle $\alpha$ pour obtenir un cône de volume maximal.
On appelle $\ell$ le rayon de la base circulaire de ce cône et $h$ sa hauteur. On rappelle que :

• le volume d'un cône de révolution de base un disque d'aire $\mathscr{A}$ et de hauteur $h$ est $\dfrac{1}{3}\mathscr{A}h$.
• la longueur d'un arc de cercle de rayon $r$ et d'angle $\theta$, exprimé en radians, est $r\theta$.

1. On choisit $R = 20$ cm.
   1. Montrer que le volume du cône, en fonction de sa hauteur $h$, est $V(h) = \dfrac{1}{3}\pi\left(400-h^2\right)h$.
   2. Justifier qu'il existe une valeur de $h$ qui rend le volume du cône maximum. Donner cette valeur.
   3. Comment découper le disque en carton pour avoir un volume maximum ? Donner un arrondi de $\alpha$ au degré près.
2. L'angle $\alpha$ dépend-il du rayon $R$ du disque en carton ?