Baccalauréat S Amérique du Sud 22 novembre 2016 - Correction Exercice 4
Page 8 sur 12
Correction de l'exercice 4 5 points
Partie A : un calcul de volume sans repère
On considère une pyramide équilatère SABCD (pyramide à base carrée dont toutes les faces latérales sont des triangles équilatéraux) représentée ci-contre. Les diagonales du carré ABCD mesurent 24 cm. On note O le centre du carré ABCD. On admettra que OS = OA. 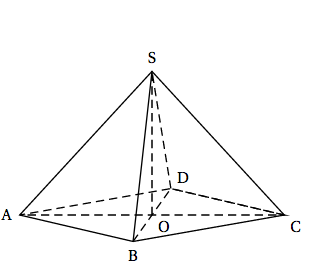
- Sans utiliser de repère, démontrer que la droite (SO) est orthogonale au plan (ABC). Les diagonales d’un carré sont de même longueur et se coupent en leur milieu.
- En déduire le volume, en cm$^3$, de la pyramide SABCD. On a $OA=\dfrac{24}{2}=12$ cm.
Par conséquent le triangle $AOB$ est rectangle et $OS=OA=OB$.
Les faces latérales de la pyramide sont des triangles équilatéraux. Par conséquent $AS=AB=BC$.
Dans le triangle $AOB$ rectangle en $O$ on applique le théorème de Pythagore :
$AB^2=AO^2+OB^2 \iff AS^2=OS^2+OA^2$
Ainsi, d’après la réciproque du théorème de Pythagore, le triangle $AOS$ est rectangle en $O$.
On montre de la même façon que le triangle $OSB$ est rectangle en $O$.
La droite $(OS)$ est donc perpendiculaire à deux droites sécantes, $(OA)$ et $(OB)$, du plan $(ABC)$ : elle est orthogonale au plan $(ABC)$.
$\quad$
En reprenant le calcul du théorème de Pythagore dans le triangle $AOB$ de la question précédente on a :
$\begin{align*} AB^2&=AO^2+OB^2 \\ &=12^2+12^2 \\ &=288
\end{align*}$
Par conséquent l’aire du carré $ABCS$ est $\mathscr{A}=AB^2=288$ cm$^2$.
Et le volume de la pyramide $SABCD$ est :
$\mathscr{V}=\dfrac{\mathscr{A}\times SO}{3}=\dfrac{288 \times 12}{3}=1~152$ cm$^3$.
$\quad$
Partie B : dans un repère
On considère le repère orthonormé $\left(\text{O}~;~\vec{\text{OA}},~ \vec{\text{OB}}, ~\vec{\text{OS}}\right)$.
- On note P et Q les milieux respectifs des segments [AS] et [BS].
- Justifier que $\vec{n}(1~;~1~;~- 3)$ est un vecteur normal au plan (PQC). Dans le repère orthonormé $\left(O;\vec{OA},\vec{OB},\vec{OS}\right)$ on a :
- En déduire une équation cartésienne du plan (PQC). Une équation cartésienne du plan $(PQC)$ est donc de la forme $x+y-3z+d=0$.
$O(0,0,0)$, $A(1,0,0)$, $B(0,1,0)$ et $S(0,0,1)$.
Les points $P$ et $Q$ sont les milieux respectifs des segments $[AS]$ et $[BS]$.
Ainsi $P\left(\dfrac{1}{2},0,\dfrac{1}{2}\right)$ et $Q\left(0,\dfrac{1}{2},\dfrac{1}{2}\right)$.
On a également $C(-1,0,0)$ car $\vec{OC}=-\vec{OA}$
Donc $\vec{PQ}\left(-\dfrac{1}{2},\dfrac{1}{2},0\right)$
et $\vec{PC}\left(-\dfrac{3}{2},0,-\dfrac{1}{2}\right)$
Ces deux vecteurs ne sont pas colinéaires car ils n’ont pas la même coordonnée nulle.
Calculons les produits scalaires :
$\vec{n}.\vec{PQ}=-\dfrac{1}{2}+\dfrac{1}{2}-3\times 0 = 0$.
$\vec{n}.\vec{PC}=-\dfrac{3}{2}-3\times \left(-\dfrac{1}{2}\right)=0$.
Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(PQC)$ : il est donc normal à ce plan.
$\quad$
Le point $C$ appartient à ce plan: ses coordonnées vérifient donc cette équation.
Ainsi $-1+0+0+d=0$ soit $d=1$.
Une équation cartésienne du plan $PQC$ est donc $x+y-3z+1=0$. - Soit H le point du plan (PQC) tel que la droite (SH) est orthogonale au plan (PQC).
- Donner une représentation paramétrique de la droite (SH). $\vec{n}$ est un vecteur directeur de la droite $(SH)$.
- Calculer les coordonnées du point H. Le point $H$ est le point d’intersection du plan $(PQC)$ et de la droite $(SH)$.
- Montrer alors que la longueur SH, en unité de longueur, est $\dfrac{2\sqrt{11}}{11}$. Ainsi :
Une représentation paramétrique de la droite $(SH)$ est donc :
$\begin{cases} x=t\\y=t \quad t \in \mathbb R\\z=1-3t\end{cases}$
$\quad$
Ces coordonnées vérifient donc les équations de la droite et du plan.
On a donc :
$\begin{cases} x=t\\y=t\\z=1-3t\\x+y-3z+1=0\end{cases}$
Par conséquent $t+t-3(1-3t)+1=0$
Soit $2t-3+9t+1=0$ d’où $11t=2$ et donc $t=\dfrac{2}{11}$.
Les coordonnées du point $H$ sont donc $\left(\dfrac{2}{11};\dfrac{2}{11};\dfrac{5}{11}\right)$.
$\quad$
$\begin{align*} SH&=\sqrt{\left(\dfrac{2}{11}\right)^2+\left(\dfrac{2}{11}\right)^2+\left(\dfrac{5}{11}-1\right)^2} \\ &=\sqrt{\dfrac{4}{121}+\dfrac{4}{121}+\dfrac{36}{121}} \\ &=\sqrt{\dfrac{44}{121}}\\ &=\dfrac{2\sqrt{11}}{11} \end{align*}$
$\quad$ - On admettra que l'aire du quadrilatère PQCD, en unité d'aire, est égale à $\dfrac{3\sqrt{11}}{8}$ Calculer le volume de la pyramide SPQCD, en unité de volume. Le volume de la pyramide $SPQCD$ est :
$\begin{align*} \mathscr{V}_1&=\dfrac{\dfrac{3\sqrt{11}}{8}\times \dfrac{2\sqrt{11}}{11}}{3} \\ &=\dfrac{1}{4}
\end{align*}$
Le volume de cette pyramide est donc de $0,25$ unité de volume.
$\quad$
Partie C : partage équitable
Pour l'anniversaire de ses deux jumelles Anne et Fanny, Madame Nova a confectionné un joli gâteau en forme de pyramide équilatère dont les diagonales du carré de base mesurent 24 cm. Elle s'apprête à le partager en deux, équitablement, en plaçant son couteau sur le sommet. C'est alors qu'Anne arrête son geste et lui propose une découpe plus originale : «Place la lame sur le milieu d'une arête, parallèlement à un côté de la base, puis coupe en te dirigeant vers le côté opposé ».
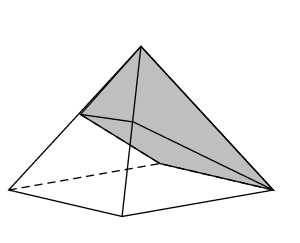
Fanny a des doutes, les parts ne lui semblent pas équitables. Est-ce le cas ? Justifier la réponse.
La découpe proposée par Anne revient à obtenir la pyramide $SPQCD$ de la partie précédente.
Le volume, en cm$^3$, de cette pyramide est donné par $12^3\times 0,25=432$ cm$^3$.
Ainsi $\dfrac{432}{1~152}\approx 0,37 \neq 0,5$.
Le partage ne sera donc pas équitable.
$\quad$
- Vues: 47264
