Baccalauréat S Nouvelle-Calédonie 19 novembre 2016 - Correction Exercice 1

Page 2 sur 12: Correction Exercice 1

Correction de l'exercice 1 (4 points)

Commun à tous les candidats

On considère la fonction $f$ définie et dérivable sur l'intervalle $[0~;~ +\infty[$ par \[f(x) = x\text{e}^{- x} - 0,1.\]

1. Déterminer la limite de $f$ en $+ \infty$.
$f(x)=x\text{e}^{-x}-0,1=\dfrac{x}{\text{e}^x}-0,1=\dfrac{1}{\dfrac{\text{e}^x}{x}}-0,1$.
Or $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} \dfrac{1}{\dfrac{\text{e}^x}{x}}=0$
Par conséquent $ \lim\limits_{x \to +\infty} f(x)=-0,1$.
$\quad$
2. Étudier les variations de $f$ sur $[0~;~+ \infty[$ et dresser le tableau de variations.
D’après l’énoncé, la fonction $f$ est dérivable sur $[0;+\infty[$.
$f'(x)=\text{e}^{-x}-x\text{e}^{-x}=(1-x)\text{e}^{-x}$
La fonction exponentielle est strictement positive sur $\mathbb R$. Le signe de $f'(x)$ ne dépend donc que de $1-x$.
Ainsi $f$ est croissante sur $[0;1]$ et décroissante sur $[1;+\infty[$.
On obtient donc le tableau de variation suivant :

3. Démontrer que l'équation $f(x) = 0$ admet une unique solution notée $\alpha$ sur l'intervalle [0 ; 1].
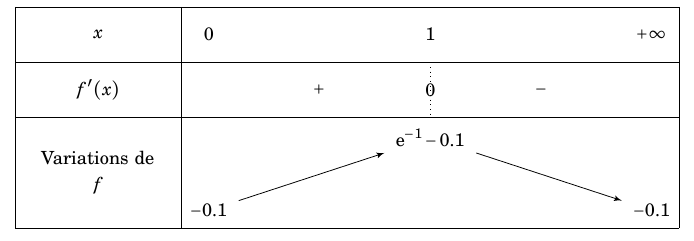
D'après le théorème de la bijection :

• $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = [\2 ; \3]$.
• $\1$ est strictement croissante sur l' intervalle $I = [\2 ; \3]$.
• $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
$\1$ réalise donc une bijection de $\left[\2;\3\right]$ sur $\left[\4;\5\right]$
$\6$ est compris entre $\1\left(\2\right)$ et $\1\left(\3\right)$, en effet $\1\left(\2\right) < \6 $ et $\1\left(\3\right) > \6 $
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $[\2 ; \3]$ .

 


On admet l'existence du nombre réel strictement positif $\beta$ tel que $\alpha < \beta$ et $f(\beta) = 0$.
On note $\mathcal{C}$ la courbe représentative de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$ dans un repère orthogonal et $\mathcal{C}'$ la courbe symétrique de $\mathcal{C}$ par rapport à l'axe des abscisses.
L'unité sur chaque axe représente 5 mètres.
Ces courbes sont utilisées pour délimiter un massif floral en forme de flamme de bougie sur lequel seront plantées des tulipes.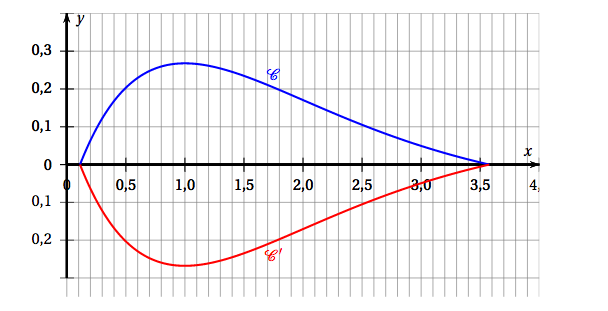


4. Démontrer que la fonction $F$, définie sur l'intervalle $[\alpha~;~\beta]$ par \[F(x) = -(x + 1)\text{e}^{- x} - 0,1x\] est une primitive de la fonction $f$ sur l'intervalle $[\alpha~;~\beta]$.
La fonction $F$ est dérivable sur $[\alpha;\beta]$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
$\begin{align*} F'(x)&=-\text{e}^{-x}-\left(-(x+1)\text{e}^{-x}\right)-0,1\\ &=-\text{e}^{-x}+(x+1)\text{e}^{-x}-0,1\\ &=(-1+x+1)\text{e}^{-x}-0,1\\ &=x\text{e}^{-x}-0,1\\ &=f(x)
\end{align*}$
$F$ est bien une primitive de la fonction $f$ sur l’intervalle $[\alpha;\beta]$.
$\quad$
5. Calculer, en unités d'aire, une valeur arrondie à $0,01$ près de l'aire du domaine compris entre les courbes $\mathcal{C}$ et $\mathcal{C}'$. On utilisera les valeurs arrondies à $0,001$ près suivantes : $\alpha \approx 0,112$ et $\beta \approx 3,577$.
Calculons dans un premier temps l’aire du domaine compris entre la courbe l’axe des abscisses, la courbe $\mathscr{C}$ et les droites d’équations $x=\alpha$ et $x=\beta$.
Cette aire vaut :
$\begin{align*} \mathscr{A}_1&=\displaystyle \int_{\alpha}^{\beta}f(x)\text{d}x \\ &=F(\beta)-F(\alpha)
\end{align*}$
Par conséquent, du fait de la symétrie des deux courbes, l’aire du domaine compris entre les courbes $\mathscr{C}$ et $\mathscr{C}’$ vaut :
$\begin{align*} \mathscr{A}&=2\left(F(\beta)-F(\alpha)\right) \\ &=2\left(-(\beta+1)\text{e}^{-\beta}-0,1\beta-\left(-(\alpha+1)\text{e}^{-\alpha}-0,1\alpha\right)\right) \\ &\approx 1,040
\end{align*}$
$\quad$
Le domaine sur chaque axe représente $5$ mètres. L’aire du domaine est donc d’environ $1,040\times 5^2$ soit $26$ m$^2$.

6. Sachant que l'on peut disposer 36 plants de tulipes par mètre carré, calculer le nombre de plants de tulipes nécessaire à la réalisation de ce massif.
On devra donc planter $36\times 26 = 936$ plants de tulipes.
$\quad$