Baccalauréat S Nouvelle-Calédonie 19 novembre 2015 - Exercice 3

Page 5 sur 10: Exercice 3

Exercice 3 5 points

Soient $x,\:y$ et $z$ trois nombres réels. On considère les implications $\left(P_1\right)$ et $\left(P_2\right)$ suivantes : \[\left(P_1\right)\qquad (x + y + z = 1) \Rightarrow \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right)\] \[\left(P_2\right) \qquad \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right) \Rightarrow (x + y + z = 1)\]

Partie A

L'implication $\left(P_2\right)$ est-elle vraie ?

Partie B

Dans l'espace, on considère le cube $ABCDEFGH$, représenté ci-dessous, et on définit le repère orthonormé $\left(A~;~ \vec{AB},~ \vec{AD},~ \vec{AE}\right)$.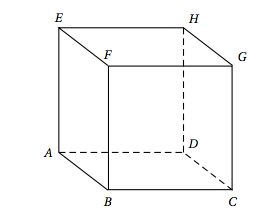

 

1. 1. Vérifier que le plan d'équation $x + y + z = 1$ est le plan ($BDE$).
   2. Montrer que la droite ($AG$) est orthogonale au plan ($BDE$).
   3. Montrer que l'intersection de la droite ($AG$) avec le plan ($BDE$) est le point $K$ de coordonnées $\left(\frac{1}{3}~;~\frac{1}{3}~;~\frac{1}{3}\right)$.
2. Le triangle $BDE$ est-il équilatéral?
3. Soit $M$ un point de l'espace.
   1. Démontrer que si $M$ appartient au plan ($BDE$), alors $AM^2 = AK^2 + MK^2$.
   2. En déduire que si $M$ appartient au plan ($BDE$), alors $AM^2 \geqslant AK^2$.
   3. Soient $x,\:y$ et $z$ des réels quelconques. En appliquant le résultat de la question précédente au point $M$ de coordonnées $(x~;~y~;~z)$, montrer que l'implication $\left(P_1\right)$ est vraie.