Baccalauréat S Nouvelle-Calédonie mars 2016 - Correction Exercice 1
Page 2 sur 10
Exercice 1 6 points
Les parties A et B sont indépendantes
Partie A
Une boite contient 200 médailles souvenir dont 50 sont argentées, les autres dorées. Parmi les argentées 60% représentent le château de Blois, 30% le château de Langeais, les autres le château de Saumur. Parmi les dorées 40% représentent le château de Blois, les autres le château de Langeais. On tire au hasard une médaille de la boite. Le tirage est considéré équiprobable et on note :
- $A$ l'évènement « la médaille tirée est argentée » ;
- $D$ l'évènement « la médaille tirée est dorée » ;
- $B$ l'évènement « la médaille tirée représente le château de Blois » ;
- $L$ l'évènement « la médaille tirée représente le château de Langeais » ;
- $S$ l'évènement « la médaille tirée représente le château de Saumur ».
- Dans cette question, on donnera les résultats sous la forme d'une fraction irréductible.
- Calculer la probabilité que la médaille tirée soit argentée et représente le château de Langeais.
- Montrer que la probabilité que la médaille tirée représente le château de Langeais est égale à $\dfrac{21}{40}$. D’après la formule des probabilités totales on a :
- Sachant que la médaille tirée représente le château de Langeais, quelle est la probabilité que celle-ci soit dorée ? On veut calculer $p_L(D)=\dfrac{p(L\cap D)}{p(L)}$ $=\dfrac{\dfrac{9}{20}}{\dfrac{21}{40}}$ $=\dfrac{6}{7}$
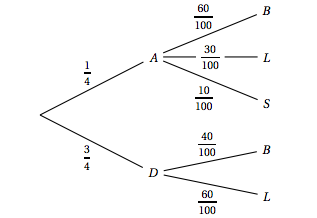
La situation peut-être modélisée par cet arbre pondéré.
On veut calculer $p(A\cap L)=\dfrac{1}{4} \times \dfrac{3}{10} = \dfrac{3}{40}$
$\quad$
$\begin{align*}
p(L)&=p(A\cap L)+p(D\cap L) \\
&=\dfrac{3}{40}+\dfrac{3}{4} \times \dfrac{3}{5} \\
&= \dfrac{21}{40}
\end{align*}$
$\quad$
$\quad$ - On veut calculer $p_S(A)$.
Les médailles représentant le château de Saumur sont exclusivement argentées. Donc $p_S(A)=1$.
$\quad$
Partie B
Une médaille est dite conforme lorsque sa masse est comprise entre $9,9$ et $10,1$ grammes. On dispose de deux machines M$_1$ et M$_2$ pour produire les médailles.
- Après plusieurs séries de tests, on estime qu'une machine M$_1$ produit des médailles dont la masse $X$ en grammes suit la loi normale d'espérance $10$ et d'écart-type $0,06$. On note $C$ l'évènement « la médaille est conforme ». Calculer la probabilité qu'une médaille produite par la machine M$_1$ ne soit pas conforme. On donnera le résultat arrondi à $10^{-3}$ près. $P(9,9 \le X \le 10,1) \approx 0,904$.
- La proportion des médailles non conformes produites par la machine M$_1$ étant jugée trop importante, on utilise une machine M$_2$ qui produit des médailles dont la masse $Y$ en grammes suit la loi normale d'espérance $\mu = 10$ et d'écart-type $\sigma$.
- Soit $Z$ la variable aléatoire égale à $\dfrac{Y - 10}{\sigma}$. Quelle est la loi suivie par la variable $Z$ ? La varaible aléatoire $Z$ suit la loi normale centrée réduite.
- Sachant que cette machine produit 6% de pièces non conformes, déterminer la valeur arrondie au millième de $\sigma$. $6\%$ des pièces ne sont pas conformes. Par conséquent $94\%$ des pièces le sont.
Donc :
$\begin{align*} P(9,9 \le Y \le 10,1) = 0,94
&\Leftrightarrow P(-0,1 \le Y -10 \le 0,1)=0,94 \\
&\Leftrightarrow P\left(-\dfrac{0,1}{\sigma} \le \dfrac{Y-10}{\sigma} \le \dfrac{0,1}{\sigma}\right) = 0,94\\
&\Leftrightarrow P\left(-\dfrac{0,1}{\sigma} \le Z \le \dfrac{0,1}{\sigma}\right) = 0,94\\
&\Leftrightarrow 2P\left(Z\le \dfrac{0,1}{\sigma}\right)-1 = 0,94 \\
&\Leftrightarrow 2P\left(Z\le \dfrac{0,1}{\sigma}\right) = 1,94 \\
&\Leftrightarrow P\left(Z\le \dfrac{0,1}{\sigma}\right) = 0,97 \\
\end{align*}$
A l’aide de la calculatrice on trouve que $\dfrac{0,1}{\sigma}\approx 1,881$ et donc $\sigma \approx 0,053$.
$\quad$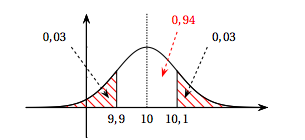
Donc $p(C)=1-P(9,9 \le X \le 10,1) \approx 0,096$.
$\quad$ En vidéo !
- Vues: 36629