BAC S 2016 de Mathématiques : Métropole 20 juin 2016 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (5 points)
Partie A
Soit $f$ la fonction définie sur $\mathbb R$ par \[f(x) = x - \ln \left(x^2 + 1\right).\]
- Résoudre dans $\mathbb R$ l'équation : $f(x) =x$. $\quad$
- Justifier tous les éléments du tableau de variations ci-dessous à l'exception de la limite de la fonction $f$ en $+ \infty$ que l'on admet.
- Montrer que, pour tout réel $x$ appartenant à $[0~;~1]$, $f(x)$ appartient à $[0~;~1]$. $f(0)=0-\ln(1)=0$
- On considère l'algorithme suivant : $$ \begin{array}{|l|c|}\hline \text{Variables }& N \text{ et } A \text{des entiers naturels ;}\\ \hline \text{Entrée } &\text{Saisir la valeur de } A \\ \hline \text{Traitement } &N \text{ prend la valeur } 0 \\ &\text{Tant que } N - \ln\left(N^2 + 1\right) < A \\ &\hspace{0,6cm} N \text{ prend la valeur } N + 1 \\ &\text{Fin tant que}\\ \hline \text{Sortie} &\text{Afficher } N \\ \hline \end{array} $$
- Que fait cet algorithme ? Cet algorithme fournir le premier entier naturel à partir duquel, pour un $A$ donné, on a $f(x)\geqslant A$.
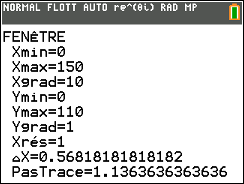
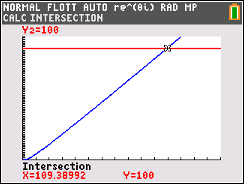
- Déterminer la valeur $N$ fournie par l'algorithme lorsque la valeur saisie pour $A$ est 100. On a $f(109) \approx 99,6$ et $f(110) \approx 100,6$.
$\quad$
Donc l’algorithme affichera $110$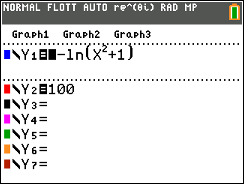
$\begin{align*} f(x)=x &\iff x-\ln\left(x^2+1\right) \\
&\iff -\ln\left(x^2+1\right)=0 \\
&\iff x^2+1=1 \\
&\iff x^2=0 \\
&\iff x=0
\end{align*}$
La solution de l’équation $f(x)=x$ est donc $0$
$\quad$
$\begin{align*} f'(x)&=1-\dfrac{2x}{x^2+1} \\
&=\dfrac{x^2+1-2x}{x^2+1}\\
&=\dfrac{(x-1)^2}{x^2+1}
\end{align*}$
Ainsi $f'(x) \geqslant 0$ en tant que quotient de nombres positifs.
Et $f'(x)=0 \iff x-1=0 \iff x=0$
La fonction $f’$ ne s’annule donc qu’en $1$ et, pour tout réel $x$ on a $f'(x) \geqslant 0$.
La fonction $f$ est par conséquent strictement croissante sur $\mathbb R$.
$\lim\limits_{x \to -\infty} x^2+1=+\infty$ or $\lim\limits_{X \to +\infty} \ln X=+\infty$.
Donc $\lim\limits_{x \to -\infty} -\ln \left(x^2+1\right)=-\infty$ et $\lim\limits_{x \to -\infty} f(x)=-\infty$.
$\quad$
La limite en $+\infty$ est admise.
$\quad$
$f(1)=1-\ln(2) <1$
La fonction $f$ est strictement croissante sur $\mathbb R$ donc, pour tout réel $x$ appartenant à $[0;1]$ on a :
$f(0) \leqslant f(x) \leqslant f(1)$ soit $0 \leqslant f(x) \leqslant 1$.
$\quad$
Partie B
Soit $\left(u_n\right)$ la suite définie par $u_0 = 1$ et, pour tout entier naturel $n$, $u_{n+1} = u_n -\ln \left(u_n^2 + 1\right)$.
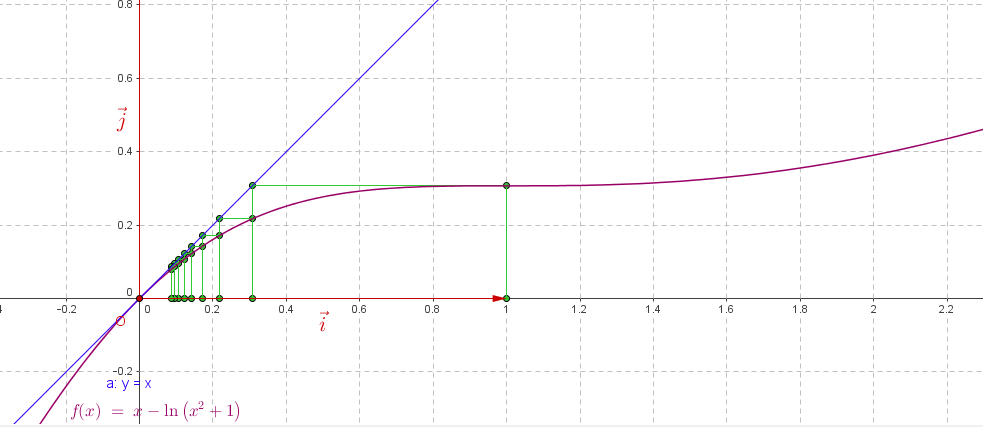
- Montrer par récurrence que, pour tout entier naturel $n$, $u_n$ appartient à $[0~;~1]$. Initialisation : $u_0=1$ donc $u_0\in[0;1]$.
- Étudier les variations de la suite $\left(u_n\right)$. Pour tout entier naturel $n$ on a :
- Montrer que la suite $\left(u_n\right)$ est convergente. La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle converge donc.
- On note $\ell$ sa limite, et on admet que $\ell$ vérifie l'égalité $f(\ell) = \ell$. En déduire la valeur de $\ell$. $\ell$ vérifie $\ell = f(\ell)$.
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n\in [0;1]$
Donc $u_{n+1}=u_n-\ln\left(u_n^2+1\right) = f \left(u_n\right)$
or, d’après la question A.3 si $\in [0;1]$ alors $f(x) \in [0;1]$.
Donc $u_{n+1} \in [0;1]$
La propriété est par conséquent vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $u_n \in [0;1]$.
$\quad$
$\begin{align*} u_{n+1}-u_n &=u_n-\ln\left(u_n^2+1\right) -u_n \\
&=-\ln\left(u_n^2+1\right)
\end{align*}$
Or $u_n^2 \geqslant 0$ donc $u_n^2+1 \geqslant 1$ et, par croissance de la fonction logarithme, $\ln\left(u_n^2+1\right) \geqslant 0$
Par conséquent $u_{n+1}-u_n \leqslant 0$.
La suite $\left(u_n\right)$ est donc décroissante.
$\quad$
$\quad$ La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle converge donc.
$\quad$
D’après la question A.1. on a alors $\ell = 0$
$\quad$
- Vues: 38887