BAC S 2016 de Mathématiques : Métropole 20 juin 2016
Exercice 1 6 points
Partie A
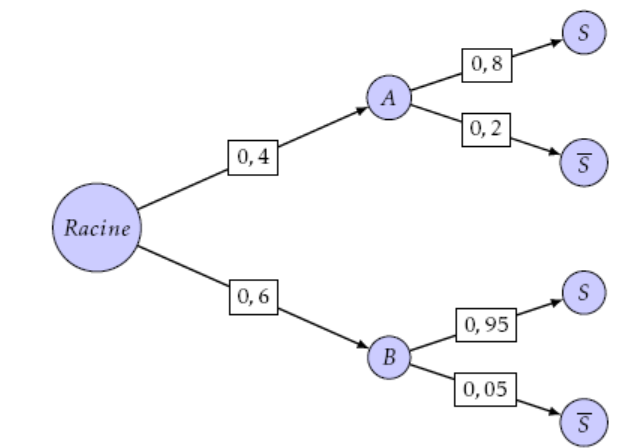
Une usine fabrique un composant électronique. Deux chaînes de fabrication sont utilisées. La chaîne A produit 40% des composants et la chaîne B produit le reste.
Une partie des composants fabriqués présentent un défaut qui les empêche de fonctionner à la vitesse prévue par le constructeur. En sortie de chaîne A, 20% des composants présentent ce défaut alors qu'en sortie de chaîne B, ils ne sont que 5%.
On choisit au hasard un composant fabriqué dans cette usine. On note :
- $A$ l'évènement « le composant provient de la chaîne A »
- $B$ l'évènement « le composant provient de la chaîne B »
- $S$ l'évènement « le composant est sans défaut »
- Montrer que la probabilité de l'évènement $S$ est $P(S) = 0,89$.
- Sachant que le composant ne présente pas de défaut, déterminer la probabilité qu'il provienne de la chaîne A. On donnera le résultat à $10^{-2}$ près.
Partie B
Des améliorations apportées à la chaîne A ont eu pour effet d'augmenter la proportion $p$ de composants sans défaut.
Afin d'estimer cette proportion, on prélève au hasard un échantillon de $400$~composants parmi ceux fabriqués par la chaîne A. Dans cet échantillon, la fréquence observée de composants sans défaut est de $0,92$.
- Déterminer un intervalle de confiance de la proportion $p$ au niveau de confiance de 95%.
- Quelle devrait être la taille minimum de l'échantillon pour qu'un tel intervalle de confiance ait une amplitude maximum de $0,02$ ?
Partie C
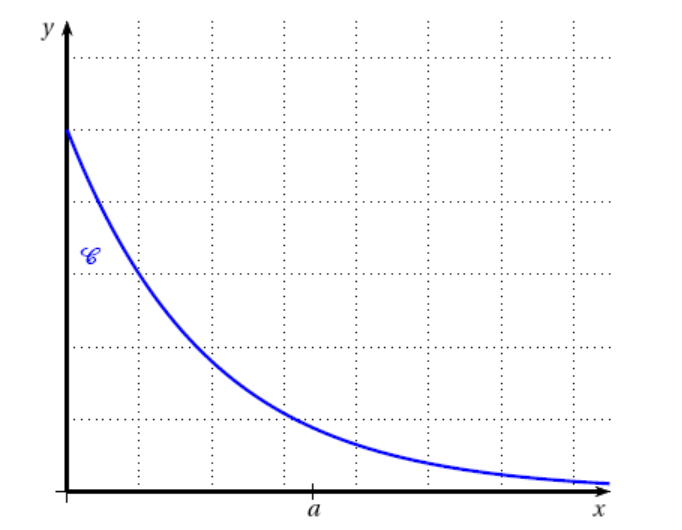
La durée de vie, en années, d'un composant électronique fabriqué dans cette usine est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda$ (où $\lambda$ est un nombre réel strictement positif). On note $f$ la fonction densité associée à la variable aléatoire $T$. On rappelle que :- pour tout nombre réel $x \geqslant 0,\: f(x) = \lambda\text{e}^{-\lambda x}$.
- pour tout nombre réel $a \geqslant 0,\: p(T \leqslant a) = \displaystyle\int_0^a f(x)\:\text{d}x$.
- La courbe représentative $\mathcal{C}$ de la fonction $f$ est donnée ci-dessous.
- Interpréter graphiquement $P(T \leqslant a)$ où $a > 0$.
- Montrer que pour tout nombre réel $t \geqslant 0 \::\: P(T \leqslant t) = 1 - \text{e}^{- \lambda t}$.
- En déduire que $\displaystyle\lim_{t \to + \infty} P(T \leqslant t) = 1$.
- On suppose que $P(T \leqslant 7) = 0,5$. Déterminer $\lambda$ à $10^{-3}$ près.
- Dans cette question on prend $\lambda = 0,099$ et on arrondit les résultats des probabilités au centième.
- On choisit au hasard un composant fabriqué dans cette usine. Déterminer la probabilité que ce composant fonctionne au moins 5 ans.
- On choisit au hasard un composant parmi ceux qui fonctionnent encore au bout de 2 ans. Déterminer la probabilité que ce composant ait une durée de vie supérieure à 7 ans.
- Donner l'espérance mathématique E($T$) de la variable aléatoire $T$ à l'unité près. Interpréter ce résultat.
Correction de l'exercice 1 (5 points)
Partie A
Une usine fabrique un composant électronique. Deux chaînes de fabrication sont utilisées. La chaîne A produit 40% des composants et la chaîne B produit le reste.
Une partie des composants fabriqués présentent un défaut qui les empêche de fonctionner à la vitesse prévue par le constructeur. En sortie de chaîne A, 20% des composants présentent ce défaut alors qu'en sortie de chaîne B, ils ne sont que 5%.
On choisit au hasard un composant fabriqué dans cette usine. On note :- $A$ l'évènement « le composant provient de la chaîne A »
- $B$ l'évènement « le composant provient de la chaîne B »
- $S$ l'évènement « le composant est sans défaut »
- Montrer que la probabilité de l'évènement $S$ est $P(S) = 0,89$. On s'aide de l'arbre pondéré ci-dessous :
- Sachant que le composant ne présente pas de défaut, déterminer la probabilité qu'il provienne de la chaîne A. On donnera le résultat à $10^{-2}$ près. On veut calculer $P_S(A)=\dfrac{P(S\cap A)}{P(S)}=\dfrac{0,4\times 0,8}{0,89}\approx 0,36$
D’après la formule des probabilités totales, on a :
$\begin{align*} P(S)&=P(S\cap A)+P(S\cap B) \\
&= 0,4 \times 0,8+0,6\times 0,95 \\
&=0,89
\end{align*}$
$\quad$
$\quad$
Partie B
Des améliorations apportées à la chaîne A ont eu pour effet d'augmenter la proportion $p$ de composants sans défaut.
Afin d'estimer cette proportion, on prélève au hasard un échantillon de $400$~composants parmi ceux fabriqués par la chaîne A. Dans cet échantillon, la fréquence observée de composants sans défaut est de $0,92$.
- Déterminer un intervalle de confiance de la proportion $p$ au niveau de confiance de 95%. $n=400 \geqslant 30$, $f=0,92$ donc $nf=368 \geqslant 5$ et $n(1-f)=32 \geqslant 5$
- Quelle devrait être la taille minimum de l'échantillon pour qu'un tel intervalle de confiance ait une amplitude maximum de $0,02$ ? Un intervalle de confiance est de la forme $\left[f-\dfrac{1}{\sqrt{n}};f+\dfrac{1}{\sqrt{n}}\right]$.
Un intervalle de confiance est alors :
$\begin{align*} I_{400}&=\left[0,92-\dfrac{1}{\sqrt{400}};0,92+\dfrac{1}{\sqrt{400}}\right] \\
&=[0,87;0,97]
\end{align*}$
Donc son amplitude est :
$\begin{align*} a&=f+\dfrac{1}{\sqrt{n}}-\left(f-\dfrac{1}{\sqrt{n}}\right) \\
&=\dfrac{2}{\sqrt{n}}
\end{align*}$
On veut donc que $\dfrac{2}{\sqrt{n}}\leqslant 0,02 \iff \dfrac{2}{\sqrt{0,02}} \leqslant\sqrt{n} \iff n \geqslant 10~000$
On doit donc avoir un échantillon d’au moins $10~000$ individus.
$\quad$
Partie C
La durée de vie, en années, d'un composant électronique fabriqué dans cette usine est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda$ (où $\lambda$ est un nombre réel strictement positif). On note $f$ la fonction densité associée à la variable aléatoire $T$. On rappelle que :- pour tout nombre réel $x \geqslant 0,\: f(x) = \lambda\text{e}^{-\lambda x}$.
- pour tout nombre réel $a \geqslant 0,\: p(T \leqslant a) = \displaystyle\int_0^a f(x)\:\text{d}x$.
- La courbe représentative $\mathcal{C}$ de la fonction $f$ est donnée ci-dessous.
- Interpréter graphiquement $P(T \leqslant a)$ où $a > 0$. $P(T\leqslant a) = \displaystyle \int_0^a f(x) \mathrm{d}x$ correspond donc à l’aire comprise entre la courbe $\mathscr{C}$, l’axe des abscisses et les droites d’équations $x=0$ et $x=a$ quand $a>0$
- Montrer que pour tout nombre réel $t \geqslant 0 \::\: P(T \leqslant t) = 1 - \text{e}^{- \lambda t}$. Pour tout $t \geqslant 0$,
- En déduire que $\displaystyle\lim_{t \to + \infty} P(T \leqslant t) = 1$. $\lim\limits_ {t \to +\infty} -\lambda t = -\infty$ donc, par composition, $\lim\limits_{t \to +\infty} \text{e}^{-\lambda t}=0$
$\quad$
$ \begin{align*} P(T\leqslant t) &= \displaystyle \int_0^t f(x) \mathrm{d}x \\
&=\big[-\text{e}^{\lambda x}\big]_0^t \\
&=-\text{e}^{-\lambda t}-(-1) \\
&=1-\text{e}^{-\lambda t}
\end{align*}$
Ainsi $\lim\limits_{t \to +\infty} P(T \leqslant t) = 1$. - On suppose que $P(T \leqslant 7) = 0,5$. Déterminer $\lambda$ à $10^{-3}$ près. On veut résoudre :
- Dans cette question on prend $\lambda = 0,099$ et on arrondit les résultats des probabilités au centième.
- On choisit au hasard un composant fabriqué dans cette usine. Déterminer la probabilité que ce composant fonctionne au moins 5 ans. On veut calculer $P(T \geqslant 5) = 1 -P(X <5) = \text{e}^{-0,099 \times 5} \approx 0,61$
- On choisit au hasard un composant parmi ceux qui fonctionnent encore au bout de 2 ans. Déterminer la probabilité que ce composant ait une durée de vie supérieure à 7 ans. $\begin{align*} P_{T\geqslant 2}(T \geqslant 7) &=P_{T\geqslant 2}(T \geqslant 5+2) \\
- Donner l'espérance mathématique E($T$) de la variable aléatoire $T$ à l'unité près. Interpréter ce résultat. $E(T) = \dfrac{1}{\lambda} =\dfrac{1}{0,099} \approx 10$.
$\quad$
&=P(T \geqslant 5) \\
&\approx 0,61
\end{align*}$
Car il s’agit d’une variable aléatoire à durée de vie sans vieillissement.
$\quad$
Cela signifie que la durée de vie moyenne d’un tel composant électronique est de $10$ ans.
$\begin{align*} P(T \leqslant 7)=0,5 &\iff 1-\text{e}^{-7\lambda }=0,5 \\
&\iff -\text{e}^{-7\lambda } = -0,5 \\
&\iff \text{e}^{-7\lambda}=0,5 \\
&\iff -7 \lambda = \ln 0,5 \\
&\iff \lambda = \dfrac{\ln 0,5}{-7}
\end{align*}$
Donc $\lambda \approx 0,099$
$\quad$
Exercice 2 4 points
Dans l'espace rapporté à un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath},~\vec{k}\right)$ on donne les points : \[\text{A}(1~;~2~;~3), \text{B}(3~;~0~;~1), \text{C}(-1~;~0~;~1), \text{D}(2~;~1~;~-1), \text{E}(-1~;~-2~;~3) \:\text{et }\: \text{F}(- 2~;~-3,4).\] Pour chaque affirmation, dire si elle est vraie ou fausse en justifiant votre réponse. Une réponse non justifiée ne sera pas prise en compte.
- Affirmation 1 : Les trois points A, B, et C sont alignés.
- Affirmation 2 : Le vecteur $\vec{n}(0~;~1~;~-1)$ est un vecteur normal au plan (ABC).
- Affirmation 3 : La droite (EF) et le plan (ABC) sont sécants et leur point d'intersection est le milieu du segment [BC].
- Affirmation 4 : Les droites (AB) et (CD) sont sécantes.
Correction de l'exercice 2 (4 points)
Dans l'espace rapporté à un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath},~\vec{k}\right)$ on donne les points : \[\text{A}(1~;~2~;~3), \text{B}(3~;~0~;~1), \text{C}(-1~;~0~;~1), \text{D}(2~;~1~;~-1), \text{E}(-1~;~-2~;~3) \:\text{et }\: \text{F}(- 2~;~-3,4).\] Pour chaque affirmation, dire si elle est vraie ou fausse en justifiant votre réponse. Une réponse non justifiée ne sera pas prise en compte.
- Affirmation 1 : Les trois points A, B, et C sont alignés.
- Affirmation 2 : Le vecteur $\vec{n}(0~;~1~;~-1)$ est un vecteur normal au plan (ABC).
- Affirmation 3 : La droite (EF) et le plan (ABC) sont sécants et leur point d'intersection est le milieu du segment [BC].
- Affirmation 4 : Les droites (AB) et (CD) sont sécantes. Affirmation 4 : fausse
Affirmation 1 : fausse
$\vec{AB}(2;-2;-2)$ et $\vec{AC}(-2;-2;-2)$
Or $\dfrac{2}{-2} \neq \dfrac{-2}{-2}$
Ces deux vecteurs ne sont pas colinéaires.
Les points $A,B$ et $C$ ne sont donc pas alignés.
$\quad$
Affirmation 2 : vraie
$\vec{n}.\vec{AB}=0\times 2+1\times (-2)+(-1) \times -2 = 0$
$\vec{n}.\vec{AC}=0\times (-2)+1\times (-2)+(-1) \times -2 = 0$
Le vecteur $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(ABC)$. Il est donc normal à ce plan.
$\quad$
Affirmation 3 : vraie
$\vec{EF}(-1;-1;1)$ donc $\vec{n}.\vec{EF}=0\times (-1)+1\times (-1) + (-1) \times 1=-2 \neq 0$
Ces deux vecteurs ne sont pas orthogonaux.
Cela signifie donc que la droite $(EF)$ et le plan $(ABC)$ sont sécants.
Le point $M$, milieu de $[BC]$, appartient naturellement au plan $(ABC)$.
Voyons s’il appartient également à $(EF)$.
On a $M(1;0;1)$
$\vec{EM}(2;2;-2)$ donc $\vec{EM}=-2\vec{EF}$.
Ces deux vecteurs sont colinéaires. Donc les points sont alignés et $M$ appartient bien à $(EF)$.
$\quad$
Une représentation paramétrique de $(AB)$ est $\begin{cases}x=1+2t\\y=2-2t \quad t\in \mathbb R\\z=3-2t\end{cases}$
On a $\vec{CD}(3;1;-2)$ donc une représentation paramétrique de $(CD)$ est $\begin{cases} x=-1+3k \\y=k \quad k\in \mathbb R \\z=1-2k\end{cases}$
Regardons si ces deux droites sont sécantes. Pour cela on va résoudre le système :
$\begin{align*} \begin{cases} 1+2t=-1+3k\\2-2t=k\\3-2t=1-2k \end{cases} &\iff \begin{cases} k=2-2t \\1+2t=-1+3(2-2t)\\3-2t=1-2(2-2t) \end{cases} \\
&\iff \begin{cases} k=2-2t \\1+2t=-1+6-6t\\3-2t=1-4+4t \end{cases} \\
&\iff \begin{cases} k=2-2t \\-4=-8t \\6=6t \end{cases} \\
&\iff \begin{cases} k=2-2t \\t=0,5 \\t=1 \end{cases}
\end{align*}$
Ce qui est impossible.
Ce système ne possède donc pas de solution et les droites $(AB)$ et $(CD)$ ne sont pas sécantes.
$\quad$
Exercice 3 5 points
Partie A
Soit $f$ la fonction définie sur $\mathbb R$ par \[f(x) = x - \ln \left(x^2 + 1\right).\]- Résoudre dans $\mathbb R$ l'équation : $f(x) =x$.
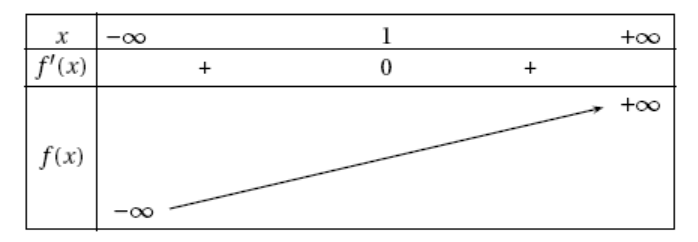
- Justifier tous les éléments du tableau de variations ci-dessous à l'exception de la limite de la fonction $f$ en $+ \infty$ que l'on admet.
- Montrer que, pour tout réel $x$ appartenant à $[0~;~1]$, $f(x)$ appartient à $[0~;~1]$.
- On considère l'algorithme suivant : $$ \begin{array}{|l|c|}\hline \text{Variables }& N \text{ et } A \text{des entiers naturels ;}\\ \hline \text{Entrée } &\text{Saisir la valeur de } A \\ \hline \text{Traitement } &N \text{ prend la valeur } 0 \\ &\text{Tant que } N - \ln\left(N^2 + 1\right) < A \\ &\hspace{0,6cm} N \text{ prend la valeur } N + 1 \\ &\text{Fin tant que}\\ \hline \text{Sortie} &\text{Afficher } N \\ \hline \end{array} $$
- Que fait cet algorithme ?
- Déterminer la valeur $N$ fournie par l'algorithme lorsque la valeur saisie pour $A$ est 100.
Partie B
Soit $\left(u_n\right)$ la suite définie par $u_0 = 1$ et, pour tout entier naturel $n$, $u_{n+1} = u_n -\ln \left(u_n^2 + 1\right)$.
- Montrer par récurrence que, pour tout entier naturel $n$, $u_n$ appartient à $[0~;~1]$.
- Étudier les variations de la suite $\left(u_n\right)$.
- Montrer que la suite $\left(u_n\right)$ est convergente.
- On note $\ell$ sa limite, et on admet que $\ell$ vérifie l'égalité $f(\ell) = \ell$. En déduire la valeur de $\ell$.
Correction de l'exercice 3 (5 points)
Partie A
Soit $f$ la fonction définie sur $\mathbb R$ par \[f(x) = x - \ln \left(x^2 + 1\right).\]- Résoudre dans $\mathbb R$ l'équation : $f(x) =x$. $\quad$
- Justifier tous les éléments du tableau de variations ci-dessous à l'exception de la limite de la fonction $f$ en $+ \infty$ que l'on admet.
- Montrer que, pour tout réel $x$ appartenant à $[0~;~1]$, $f(x)$ appartient à $[0~;~1]$. $f(0)=0-\ln(1)=0$
- On considère l'algorithme suivant : $$ \begin{array}{|l|c|}\hline \text{Variables }& N \text{ et } A \text{des entiers naturels ;}\\ \hline \text{Entrée } &\text{Saisir la valeur de } A \\ \hline \text{Traitement } &N \text{ prend la valeur } 0 \\ &\text{Tant que } N - \ln\left(N^2 + 1\right) < A \\ &\hspace{0,6cm} N \text{ prend la valeur } N + 1 \\ &\text{Fin tant que}\\ \hline \text{Sortie} &\text{Afficher } N \\ \hline \end{array} $$
- Que fait cet algorithme ? Cet algorithme fournir le premier entier naturel à partir duquel, pour un $A$ donné, on a $f(x)\geqslant A$.
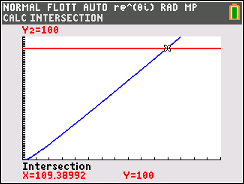
- Déterminer la valeur $N$ fournie par l'algorithme lorsque la valeur saisie pour $A$ est 100. On a $f(109) \approx 99,6$ et $f(110) \approx 100,6$.
$\quad$
Donc l’algorithme affichera $110$
$\begin{align*} f(x)=x &\iff x-\ln\left(x^2+1\right) \\
&\iff -\ln\left(x^2+1\right)=0 \\
&\iff x^2+1=1 \\
&\iff x^2=0 \\
&\iff x=0
\end{align*}$
La solution de l’équation $f(x)=x$ est donc $0$
$\quad$
$\begin{align*} f'(x)&=1-\dfrac{2x}{x^2+1} \\
&=\dfrac{x^2+1-2x}{x^2+1}\\
&=\dfrac{(x-1)^2}{x^2+1}
\end{align*}$
Ainsi $f'(x) \geqslant 0$ en tant que quotient de nombres positifs.
Et $f'(x)=0 \iff x-1=0 \iff x=0$
La fonction $f’$ ne s’annule donc qu’en $1$ et, pour tout réel $x$ on a $f'(x) \geqslant 0$.
La fonction $f$ est par conséquent strictement croissante sur $\mathbb R$.
$\lim\limits_{x \to -\infty} x^2+1=+\infty$ or $\lim\limits_{X \to +\infty} \ln X=+\infty$.
Donc $\lim\limits_{x \to -\infty} -\ln \left(x^2+1\right)=-\infty$ et $\lim\limits_{x \to -\infty} f(x)=-\infty$.
$\quad$
La limite en $+\infty$ est admise.
$\quad$
$f(1)=1-\ln(2) <1$
La fonction $f$ est strictement croissante sur $\mathbb R$ donc, pour tout réel $x$ appartenant à $[0;1]$ on a :
$f(0) \leqslant f(x) \leqslant f(1)$ soit $0 \leqslant f(x) \leqslant 1$.
$\quad$
Partie B
Soit $\left(u_n\right)$ la suite définie par $u_0 = 1$ et, pour tout entier naturel $n$, $u_{n+1} = u_n -\ln \left(u_n^2 + 1\right)$.
- Montrer par récurrence que, pour tout entier naturel $n$, $u_n$ appartient à $[0~;~1]$. Initialisation : $u_0=1$ donc $u_0\in[0;1]$.
- Étudier les variations de la suite $\left(u_n\right)$. Pour tout entier naturel $n$ on a :
- Montrer que la suite $\left(u_n\right)$ est convergente. La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle converge donc.
- On note $\ell$ sa limite, et on admet que $\ell$ vérifie l'égalité $f(\ell) = \ell$. En déduire la valeur de $\ell$. $\ell$ vérifie $\ell = f(\ell)$.
La propriété est vraie au rang $0$
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $u_n\in [0;1]$
Donc $u_{n+1}=u_n-\ln\left(u_n^2+1\right) = f \left(u_n\right)$
or, d’après la question A.3 si $\in [0;1]$ alors $f(x) \in [0;1]$.
Donc $u_{n+1} \in [0;1]$
La propriété est par conséquent vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $u_n \in [0;1]$.
$\quad$
$\begin{align*} u_{n+1}-u_n &=u_n-\ln\left(u_n^2+1\right) -u_n \\
&=-\ln\left(u_n^2+1\right)
\end{align*}$
Or $u_n^2 \geqslant 0$ donc $u_n^2+1 \geqslant 1$ et, par croissance de la fonction logarithme, $\ln\left(u_n^2+1\right) \geqslant 0$
Par conséquent $u_{n+1}-u_n \leqslant 0$.
La suite $\left(u_n\right)$ est donc décroissante.
$\quad$
$\quad$ La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle converge donc.
$\quad$
D’après la question A.1. on a alors $\ell = 0$
$\quad$
Exercice 4 5 points
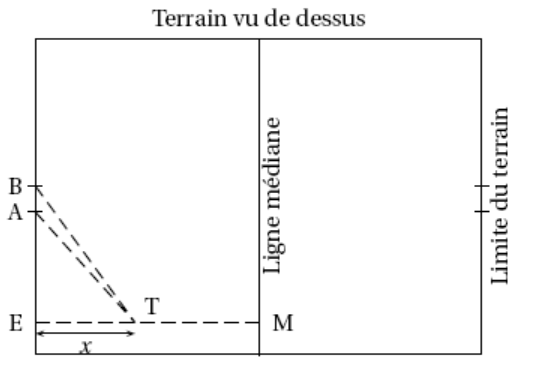
Lors d'un match de rugby, un joueur doit transformer un essai qui a été marqué au point E (voir figure ci-dessous) situé à l'extérieur du segment [AB]. La transformation consiste à taper le ballon par un coup de pied depuis un point T que le joueur a le droit de choisir n'importe où sur le segment [EM] perpendiculaire à la droite (AB) sauf en E. La transformation est réussie si le ballon passe entre les poteaux repérés par les points A et B sur la figure.
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point T qui rend l'angle $\widehat{\text{ATB}}$ le plus grand possible.
Le but de cet exercice est donc de rechercher s'il existe une position du point T sur le segment [EM] pour laquelle l'angle $\widehat{\text{ATB}}$ est maximum et, si c'est le cas, de déterminer une valeur approchée de cet angle. Dans toute la suite, on note $x$ la longueur ET, qu'on cherche à déterminer.
Les dimensions du terrain sont les suivantes : EM = 50 m, EA = 25 m et AB = 5,6 m . On note $\alpha$ la mesure en radian de l'angle $\widehat{\text{ETA}}$, $\beta$ la mesure en radian de l'angle $\widehat{\text{ETB}}$ et $\gamma$ la mesure en radian de l'angle $\widehat{\text{ATB}}$.
- En utilisant les triangles rectangles ETA et ETB ainsi que les longueurs fournies, exprimer $\tan \alpha$ et $\tan \beta$ en fonction de $x$. La fonction tangente est définie sur l'intervalle $\left]0~;~\dfrac{\pi}{2}\right[$ par $\tan x = \dfrac{\sin x}{\cos x}$.
- Montrer que la fonction tan est strictement croissante sur l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$.
- L'angle $\widehat{\text{ATB}}$ admet une mesure $\gamma$ appartenant à l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$, résultat admis ici, que l'on peut observer sur la figure. On admet que, pour tous réels $a$ et $b$ de l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$, $\tan(a - b) = \dfrac{\tan a - \tan b}{1 + \tan a \times \tan b}$. Montrer que $\tan \gamma = \dfrac{5,6x}{x^2 + 765}$.
- L'angle $\widehat{\text{ATB}}$ est maximum lorsque sa mesure $\gamma$ est maximale. Montrer que cela correspond à un minimum sur l'intervalle ]0 ; 50] de la fonction $f$ définie par : $f(x)= x+ \dfrac{765}{x}$. Montrer qu'il existe une unique valeur de $x$ pour laquelle l'angle $\widehat{\text{ATB}}$ est maximum et déterminer cette valeur de $x$ au mètre près ainsi qu'une mesure de l'angle $\widehat{\text{ATB}}$ à $0,01$ radian près.
Correction de l'exercice 4 5 points
Lors d'un match de rugby, un joueur doit transformer un essai qui a été marqué au point E (voir figure ci-dessous) situé à l'extérieur du segment [AB]. La transformation consiste à taper le ballon par un coup de pied depuis un point T que le joueur a le droit de choisir n'importe où sur le segment [EM] perpendiculaire à la droite (AB) sauf en E. La transformation est réussie si le ballon passe entre les poteaux repérés par les points A et B sur la figure.
Pour maximiser ses chances de réussite, le joueur tente de déterminer la position du point T qui rend l'angle $\widehat{\text{ATB}}$ le plus grand possible.
Le but de cet exercice est donc de rechercher s'il existe une position du point T sur le segment [EM] pour laquelle l'angle $\widehat{\text{ATB}}$ est maximum et, si c'est le cas, de déterminer une valeur approchée de cet angle. Dans toute la suite, on note $x$ la longueur ET, qu'on cherche à déterminer.
Les dimensions du terrain sont les suivantes : EM = 50 m, EA = 25 m et AB = 5,6 m . On note $\alpha$ la mesure en radian de l'angle $\widehat{\text{ETA}}$, $\beta$ la mesure en radian de l'angle $\widehat{\text{ETB}}$ et $\gamma$ la mesure en radian de l'angle $\widehat{\text{ATB}}$.
- En utilisant les triangles rectangles ETA et ETB ainsi que les longueurs fournies, exprimer $\tan \alpha$ et $\tan \beta$ en fonction de $x$. La fonction tangente est définie sur l'intervalle $\left]0~;~\dfrac{\pi}{2}\right[$ par $\tan x = \dfrac{\sin x}{\cos x}$. Dans le triangle $ETA$ rectangle en $E$ on a : $\tan \alpha = \tan \widehat{ETA}=\dfrac{EA}{ET} = \dfrac{25}{x}$.
- Montrer que la fonction tan est strictement croissante sur l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$. La fonction $\tan$ est dérivable sur $\left]0;\dfrac{\pi}{2}\right[$ en tant que quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas sur cet intervalle.
- L'angle $\widehat{\text{ATB}}$ admet une mesure $\gamma$ appartenant à l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$, résultat admis ici, que l'on peut observer sur la figure. On admet que, pour tous réels $a$ et $b$ de l'intervalle $\left]0~;~ \dfrac{\pi}{2}\right[$, $\tan(a - b) = \dfrac{\tan a - \tan b}{1 + \tan a \times \tan b}$. Montrer que $\tan \gamma = \dfrac{5,6x}{x^2 + 765}$. $\quad$
- L'angle $\widehat{\text{ATB}}$ est maximum lorsque sa mesure $\gamma$ est maximale. Montrer que cela correspond à un minimum sur l'intervalle ]0 ; 50] de la fonction $f$ définie par : $f(x)= x+ \dfrac{765}{x}$. Montrer qu'il existe une unique valeur de $x$ pour laquelle l'angle $\widehat{\text{ATB}}$ est maximum et déterminer cette valeur de $x$ au mètre près ainsi qu'une mesure de l'angle $\widehat{\text{ATB}}$ à $0,01$ radian près. La fonction $\tan$ est strictement croissante sur $\left]0;\dfrac{\pi}{2}\right[$ donc $\gamma$ est maximal quand $\tan \gamma$ l’est c’est-à-dire quand $x \mapsto 5,6\dfrac{x}{x^2+765}$ est maximale et donc, du fait de la décroissance de la fonction inverse, quand $x \mapsto \dfrac{x^2+765}{x}$ est minimale ce qui revient à $f$ minimale.
$\quad$
Dans le triangle $ETB$ rectangle en $E$ on a : $\tan \beta = \tan \widehat{ETB}=\dfrac{EB}{ET} = \dfrac{30,6}{x}$.
$\quad$
Ainsi $\tan'(x)=\dfrac{\cos x \times \cos x-\sin x \times (-\sin x)}{\cos^2 x} = \dfrac{1}{\cos^2 x}$
Car, pour tout réel $x$ on a $\sin^2 x+\cos^2 x=1$.
Un carré étant toujours positif, $\tan'(x) > 0$ et la fonction $\tan$ est strictement croissante sur $\left]0;\dfrac{\pi}{2}\right[$.
$\quad$
$\begin{align*} \tan \gamma &=\tan \widehat{ATB} \\
&=\tan(\beta-\alpha) \\
&=\dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \times \tan \alpha} \\
&= \dfrac{\dfrac{30,6}{x}-\dfrac{25}{x}}{1+\dfrac{30,6}{x}\times \dfrac{25}{x}} \\
&=\dfrac{5,6}{x+\dfrac{765}{x}} \\
&=\dfrac{5,6x}{x^2+765}
\end{align*}$
$f$ est dérivable sur $]0;50]$ en tant que somme de fonctions dérivables sur cet intervalle.
On a donc $f'(x)=1-\dfrac{765}{x^2}=\dfrac{x^2-765}{x^2}$.
Donc sur l’intervalle $]0;50]$, $f'(x) \leqslant 0$ sur $\left]0;\sqrt{765}\right]$ et $f'(x) \geqslant 0$ sur $\left[\sqrt{365};50\right]$.
La fonction $f$ admet alors un minimum pour $x_0=\sqrt{365} \approx 28$.
Ce minimum est unique.
$\quad$
En prenant $x=28$ m on trouve $\tan \gamma \approx 0,101$ et donc $\gamma \approx 0,10$ radian.
Spécialité 5 points
Pour tout couple d'entiers relatifs non nuls $(a,\:b)$, on note pgcd$(a,\:b)$ le plus grand diviseur commun de $a$ et $b$. Le plan est muni d'un repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$.
- Exemple. Soit $\Delta_1$ la droite d'équation $y = \dfrac{5}{4} x - \dfrac{2}{3}$.
- Montrer que si $(x,\:y)$ est un couple d'entiers relatifs alors l'entier $15x - 12y$ est divisible par $3$.
- Existe-il au moins un point de la droite $\Delta_1$ dont les coordonnées sont deux entiers relatifs ? Justifier.
On considère désormais une droite $\Delta$ d'équation $(E) \::\: y = \dfrac{m}{n} x - \dfrac{p}{q}$ où $m, n, p$ et $q$ sont des entiers relatifs non nuls tels que pgcd$(m,\: n) = \text{pgcd}(p,\: q) = 1$. Ainsi, les coefficients de l'équation $(E)$ sont des fractions irréductibles et on dit que $\Delta$ est une droite rationnelle. Le but de l'exercice est de déterminer une condition nécessaire et suffisante sur $m, n, p$ et $q$ pour qu'une droite rationnelle $\Delta$ comporte au moins un point dont les coordonnées sont deux entiers relatifs. - On suppose ici que la droite $\Delta$ comporte un point de coordonnées $\left(x_0,\:y_0\right)$ où $x_0$ et $y_0$ sont des entiers relatifs.
- En remarquant que le nombre $n y_0 - m x_0$ est un entier relatif, démontrer que $q$ divise le produit $np$.
- En déduire que $q$ divise $n$.
- Réciproquement, on suppose que $q$ divise $n$, et on souhaite trouver un couple $\left(x_0,\:y_0\right)$ d'entiers relatifs tels que $y_0 = \dfrac{m}{n}x_0 - \dfrac{p}{q}$.
- On pose $n = qr$, où $r$ est un entier relatif non nul. Démontrer qu'on peut trouver deux entiers relatifs $u$ et $v$ tels que $qru - mv = 1$.
- En déduire qu'il existe un couple $\left(x_0,\:y_0\right)$ d'entiers relatifs tels que $y_0 = \dfrac{m}{n} x_0 - \dfrac{p}{q}$.
- Soit $\Delta$ la droite d'équation $y = \dfrac{3}{8} x - \dfrac{7}{4}$. Cette droite possède-t-elle un point dont les coordonnées sont des entiers relatifs ? Justifier.
- On donne l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{Variables :}& M, N, P, Q :\text{ entiers relatifs-nom nuls, tels que pgcd} (M,\: N) \text{ = pgcd}(P,\:Q) = 1 \\ & X : \text{entier naturel}\\ \text{Entrées :} &\text{ Saisir les valeurs de } M, N, P, Q \\ \text{Traitement et sorties :}&\\ &\text{Si }Q \text{ divise } N \text{ alors}\\ &\begin{array}{|l} X \text{ prend la valeur } 0 \\ \text{ Tant que } \left(\dfrac{M}{N}X - \dfrac{P}{Q}\right) \text{n'est pas entier} \\ \text{et } \left(-\dfrac{M}{N}X - \dfrac{P}{Q}\right) \text{n'est pas entier} \text{ faire}\\ \hspace{0,5cm}\begin{array}{|l} X \text{ prend la valeur } X + 1 \end{array}\\ \text{ Fin tant que} \\ \text{Si } \dfrac{M}{N}X - \dfrac{P}{Q} \text{ est entier alors }\\ \hspace{0,5cm}\begin{array}{|l} \text{Afficher } X, \dfrac{M}{N}X - \dfrac{P}{Q} \end{array}\\ \text{ Sinon}\\ \hspace{0,5cm}\begin{array}{|l} \text{ Afficher } -X, - \dfrac{M}{N}X - \dfrac{P}{Q} \end{array}\\ \text{ Fin Si }\\ \end{array}\\ &\text{ Sinon }\\ &\begin{array}{|l} \text{ Afficher « Pas de solution » } \end{array}\\ &\text{Fin Si }\\\hline \end{array} $$
- Justifier que cet algorithme se termine pour toute entrée de $M, N, P, Q$, entiers relatifs non nuls tels que pgcd$(M,\: N)$ = pgcd$(P,\: Q) = 1$.
- Que permet-il d'obtenir ?
Correction de l'exercice de Spécialité 5 points
Pour tout couple d'entiers relatifs non nuls $(a,\:b)$, on note pgcd$(a,\:b)$ le plus grand diviseur commun de $a$ et $b$. Le plan est muni d'un repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$.
- Exemple. Soit $\Delta_1$ la droite d'équation $y = \dfrac{5}{4} x - \dfrac{2}{3}$.
- Montrer que si $(x,\:y)$ est un couple d'entiers relatifs alors l'entier $15x - 12y$ est divisible par $3$. Si $(x,y)$ est un couple d’entier relatifs alors :
- Existe-il au moins un point de la droite $\Delta_1$ dont les coordonnées sont deux entiers relatifs ? Justifier. Soit $(x,y)$ les coordonnées d’un point de la droite $\Delta_1$.
$15x-12y=3\times (5x-4y)$ est un multiple de $3$ et est donc divisible par $3$.
$\quad$
Alors :
$\begin{align*} y=\dfrac{5}{4}x-\dfrac{2}{3} &\iff 12y=15x-8 \\
&\iff 15x-12y=8
\end{align*}$
Or $8$ n’est pas divisible par $3$.
Aucun des points de la droite $\Delta_1$ n’a ses deux coordonnées entières.
$\quad$
On considère désormais une droite $\Delta$ d'équation $(E) \::\: y = \dfrac{m}{n} x - \dfrac{p}{q}$ où $m, n, p$ et $q$ sont des entiers relatifs non nuls tels que pgcd$(m,\: n) = \text{pgcd}(p,\: q) = 1$. Ainsi, les coefficients de l'équation $(E)$ sont des fractions irréductibles et on dit que $\Delta$ est une droite rationnelle. Le but de l'exercice est de déterminer une condition nécessaire et suffisante sur $m, n, p$ et $q$ pour qu'une droite rationnelle $\Delta$ comporte au moins un point dont les coordonnées sont deux entiers relatifs. - On suppose ici que la droite $\Delta$ comporte un point de coordonnées $\left(x_0,\:y_0\right)$ où $x_0$ et $y_0$ sont des entiers relatifs.
- En remarquant que le nombre $n y_0 - m x_0$ est un entier relatif, démontrer que $q$ divise le produit $np$. Le couple $\left(x_0,y_0\right)$ vérifie $y_0=\dfrac{m}{n}x_0-\dfrac{p}{q}$
- En déduire que $q$ divise $n$. $p$ et $q$ sont premiers entre eux et $q$ divise $np$ par conséquent, d’après le théorème de Gauss, $q$ divise $n$.
Donc $ny_0=mx_0-\dfrac{pn}{q}$
Soit $ny_0-mx_0=-\dfrac{pn}{q}$
Puisque $n, y_0, m$ et $x_0$ dont des entiers naturels alors $ny_0-mx_0$ aussi et par conséquent $\dfrac{np}{q}$ l’est également.
Cela signifie que $q$ divise $np$.
$\quad$
- Réciproquement, on suppose que $q$ divise $n$, et on souhaite trouver un couple $\left(x_0,\:y_0\right)$ d'entiers relatifs tels que $y_0 = \dfrac{m}{n}x_0 - \dfrac{p}{q}$.
- On pose $n = qr$, où $r$ est un entier relatif non nul. Démontrer qu'on peut trouver deux entiers relatifs $u$ et $v$ tels que $qru - mv = 1$. $n$ et $m$ sont premiers entre eux. D’après le théorème de Bezout, il existe donc deux entiers relatifs $a$ et $b$ tels que :
- En déduire qu'il existe un couple $\left(x_0,\:y_0\right)$ d'entiers relatifs tels que $y_0 = \dfrac{m}{n} x_0 - \dfrac{p}{q}$. On veut trouver un couple d’entiers relatifs $\left(x_0,y_0\right)$ tels que :
$an+bm=1$
Puisque $n=qr$ on obtient $aqr+bm=1$
Il suffit donc de prendre $u=a$ et $v=-b$ pour obtenir $qru-mv=1$.
$\quad$
$\begin{align*} y_0=\dfrac{mx_0}{n}-\dfrac{p}{q} &\iff ny_0=mx_0-\dfrac{np}{q} \\
&\iff ny_0-mx_0=-pr \end{align*}$
Or il existe un couple d’entiers relatifs $(u,v)$ tel que :
$\begin{align*} qru-mv=1 &\iff -pr(qru-mv)=-pr \\
&\iff -prnu+prmv=-pr
\end{align*}$
Prenons alors $y_0=-pru$ et $x_0=-prv$
$\quad$ - Soit $\Delta$ la droite d'équation $y = \dfrac{3}{8} x - \dfrac{7}{4}$. Cette droite possède-t-elle un point dont les coordonnées sont des entiers relatifs ? Justifier. Si $y=\dfrac{3}{8}x-\dfrac{7}{4}$
- On donne l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{Variables :}& M, N, P, Q :\text{ entiers relatifs-nom nuls, tels que pgcd} (M,\: N) \text{ = pgcd}(P,\:Q) = 1 \\ & X : \text{entier naturel}\\ \text{Entrées :} &\text{ Saisir les valeurs de } M, N, P, Q \\ \text{Traitement et sorties :}&\\ &\text{Si }Q \text{ divise } N \text{ alors}\\ &\begin{array}{|l} X \text{ prend la valeur } 0 \\ \text{ Tant que } \left(\dfrac{M}{N}X - \dfrac{P}{Q}\right) \text{n'est pas entier} \\ \text{et } \left(-\dfrac{M}{N}X - \dfrac{P}{Q}\right) \text{n'est pas entier} \text{ faire}\\ \hspace{0,5cm}\begin{array}{|l} X \text{ prend la valeur } X + 1 \end{array}\\ \text{ Fin tant que} \\ \text{Si } \dfrac{M}{N}X - \dfrac{P}{Q} \text{ est entier alors }\\ \hspace{0,5cm}\begin{array}{|l} \text{Afficher } X, \dfrac{M}{N}X - \dfrac{P}{Q} \end{array}\\ \text{ Sinon}\\ \hspace{0,5cm}\begin{array}{|l} \text{ Afficher } -X, - \dfrac{M}{N}X - \dfrac{P}{Q} \end{array}\\ \text{ Fin Si }\\ \end{array}\\ &\text{ Sinon }\\ &\begin{array}{|l} \text{ Afficher « Pas de solution » } \end{array}\\ &\text{Fin Si }\\\hline \end{array} $$
- Justifier que cet algorithme se termine pour toute entrée de $M, N, P, Q$, entiers relatifs non nuls tels que pgcd$(M,\: N)$ = pgcd$(P,\: Q) = 1$. Si $Q$ ne divise pas $N$ alors on ne rentre pas dans la boucle Tant que et l’algorithme s’arrête.
- Que permet-il d'obtenir ? Cet algorithme permet de trouver un point de $\Delta$ dont les coordonnées sont entières.
Si $Q$ divise $N$ alors d’après la question 3.b. il existe pour tous les entiers relatifs $m,n,p,q$ tels que
pgcd$(m,n)=$pgcd$(p,q)=1$ et $q$ divise $n$ un couple d’entiers relatifs $\left(x_0;y_0\right)$ tels que $y_0=\dfrac{m}{n}x_0-\dfrac{p}{q}$.
On va donc trouver un entier relatif $x_0$ tel que $\dfrac{m}{n}x_0-\dfrac{p}{q}$ est entier.
Cet entier est soit positif, soit négatif.
La boucle Tant que s’arrête si l’une des deux conditions n’est pas vérifiée ce qui, d’après ce qui vient d’être dit, arrivera au moins une fois.
$\quad$
$\quad$
Alors $m=3$, $n=8$, $p=7$ et $q=4$.
pgcd$(3,8)=1$ et pgcd$(7,4)=1$
$4$ divise $8$ donc cette droite possède bien un point dont les coordonnées sont des entiers relatifs.
$\quad$
- Vues: 19852