BAC S 2016 de Mathématiques : Polynésie 10 juin 2016 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
Pour chacune des cinq propositions suivantes, indiquer si elle est vraie ou fausse et justifier la réponse choisie.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
-
Proposition 1 :
Dans le plan complexe muni d'un repère orthonormé, les points A, B et C d'affixes respectives $z_{\text{A}} = \sqrt{2} + 3\text{i},\: z_{\text{B}} = 1 + \text{i}$ et $z_{\text{C}} = - 4\text{i}$ ne sont pas alignés.Proposition 1 : vraie
L’affixe du vecteur $\vec{AB}$ est $z_1=z_B-z_A=1+\text{i}-\sqrt{2}-3\text{i} = 1-\sqrt{2}-2\text{i}$
L’affixe du vecteur $\vec{AC}$ est $z_2=z_C-z_A=-4\text{i}-\sqrt{2}-3\text{i} = -\sqrt{2}-7\text{i}$.
$\dfrac{1-\sqrt{2}}{-\sqrt{2}} \approx 0,293$
$\dfrac{-2}{-7}\approx 0,286$
Les vecteurs ne sont donc pas colinéaires et les points ne sont pas alignés.
Remarque : On pouvait également utiliser l’argument de $\dfrac{z_B-z_A}{z_C-z_A}$.
$\quad$ -
Proposition 2 :
Il n'existe pas d'entier naturel $n$ non nul tel que $\left[\text{i}(1 + \text{i})\right]^{2n}$ soit un réel strictement positif.Proposition 2 : fausse
$\text{i}(1+\text{i})=-1+\text{i}$
$|-1+\text{i}|=\sqrt{2}$
Donc $-1+\text{i}=\sqrt{2}\left(-\dfrac{1}{\sqrt{2}}+\dfrac{\text{i}}{\sqrt{2}}\right) = \sqrt{2}\text{e}^{3\text{i}\pi/4}$
Donc $\left[\text{i}(1+\text{i})\right]^{2n}=\sqrt{2}^{2n}\text{e}^{3n\text{i}\pi/2}$
Donc si $\dfrac{3n}{2}$ est un entier pair la proposition sera fausse.
Il suffit de prendre $n=4$ car $\dfrac{3\times 4}{2}=6$.
On vérifie $\left[\text{i}(1+\text{i})\right]^{2\times 4}=16$.
$\quad$ - ABCDEFGH est un cube de côté 1. Le point L est tel que $\vec{\text{EL}} = \dfrac{1}{3}\vec{\text{EF}}$
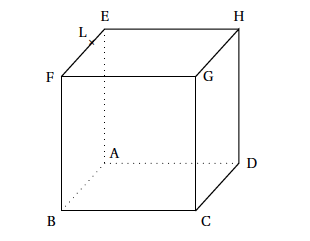
Proposition 3
La section du cube par le plan (BDL) est un triangle.Proposition 3 : fausse
- Méthode 1 :
Les plans $(EFG)$ et $(ABC)$ sont parallèles.
Donc les intersections de ces plans avec le plan $(BDL)$ sont parallèles.
Il existe donc un point $M$ appartenant à $[EH]$ tel que $(LM)$ et $(BD)$ soient parallèles.
L’intersection du cube par le plan $(BDL)$ contient donc au moins quatre points : $B$, $D$, $M$ et $L$.
$\quad$ - Méthode 2 : on trace la section !
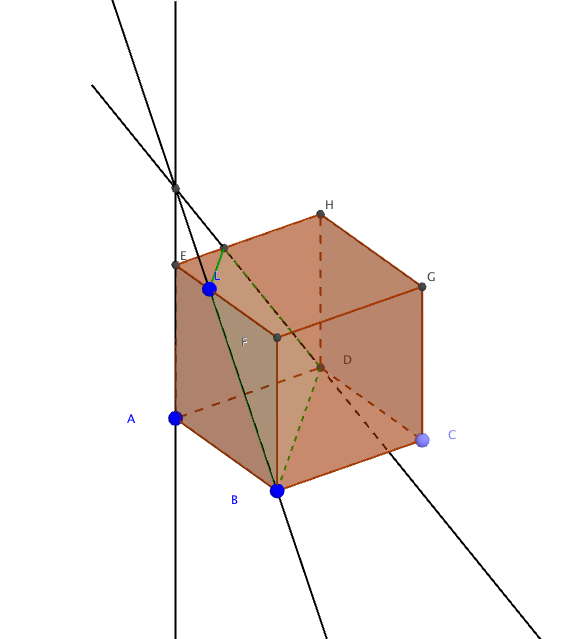
Proposition 4
Le triangle DBL est rectangle en B.Proposition 4 : fausse
On se place dans le repère $\left(B;\vec{BC},\vec{BA},\vec{BF}\right)$.
On a ainsi $B(0;0;0)$, $D(1;1;0)$ et $L\left(0;\dfrac{2}{3};1\right)$.
Par conséquent $\vec{BD}(1;1;0)$ et $\vec{BL}\left(0;\dfrac{2}{3};1\right)$.
Donc $\vec{BD}.\vec{BL}=0+\dfrac{2}{3}+0=\dfrac{2}{3}\neq 0$.
Le triangle $DBL$ n’est donc pas rectangle en $B$. - Méthode 1 :
- On considère la fonction $f$ définie sur l'intervalle [2 ; 5] et dont on connaît le tableau de variations donné ci-dessous :
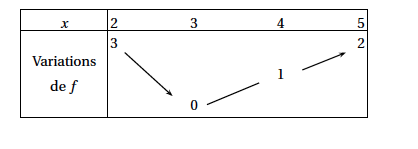 Proposition 5 : fausse
Proposition 5 : fausseProposition 5 :
L'intégrale $\displaystyle\int_2^5 f(x)\:\text{d}x$ est comprise entre $1,5$ et $6$.
On va proposer un contre-exemple qui possède une aire très proche de $1$.
On définit la fonction $f$ par morceau comme la fonction dont la représentation graphique est constitué des segments $[AB]$, $[BC]$, $[CD]$, $[DE]$, $[EF]$ et $[FG]$
Avec $A(2;3)$, $B(2,000001;0,000001)$, $C(3;0)$, $D(3,99999;0,000001)$, $E(4;1)$, $F(4,99999;1,000001)$ et $G(5;2)$.
$\displaystyle \int_2^5 f(x)\mathrm{d}x$ correspond à l’aire comprise entre la courbe représentant $f$, l’axe des abscisses et les droites d’équation $x=2$ et $ x=5$.
Dans l’exemple choisi, cela correspond à la somme de six triangles et de quatre carrés :
– un triangle rectangle de côté : $2,999999\times 0,000001$
– cinq triangles rectangles isocèles de côté $0,000001$
– trois carrés de côté $0,000001$
– un carré de côté $1$
L’aire est alors d’environ $1,0000015 <1,5$
Remarque : On pouvait évidemment utiliser d’autres valeurs plus agréables à manipuler; le but était d’avoir une situation « limite » de ce genre :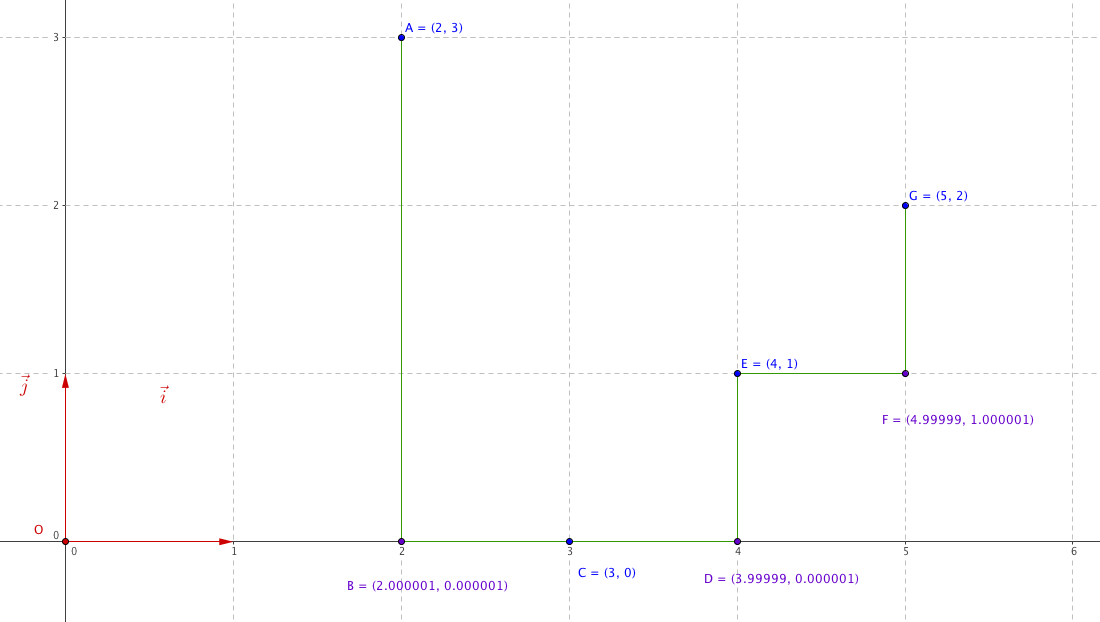
- Vues: 33223
