BAC S 2016 de Mathématiques : Polynésie 10 juin 2016 - Correction Exercice 3
Correction de l'exercice 3 (5 points)
Partie A
Un astronome responsable d'un club d'astronomie a observé le ciel un soir d'août 2015 pour voir des étoiles filantes. Il a effectué des relevés du temps d'attente entre deux apparitions d'étoiles filantes. Il a alors modélisé ce temps d'attente, exprimé en minutes, par une variable aléatoire $T$ qui suit une loi exponentielle de paramètre $\lambda$. En exploitant les données obtenues, il a établi que $\lambda = 0,2$. Il prévoit d'emmener un groupe de nouveaux adhérents de son club lors du mois d'août 2016 pour observer des étoiles filantes. Il suppose qu'il sera dans des conditions d'observation analogues à celles d'août 2015. L'astronome veut s'assurer que le groupe ne s'ennuiera pas et décide de faire quelques calculs de probabilités dont les résultats serviront à animer la discussion.
- Lorsque le groupe voit une étoile filante, vérifier que la probabilité qu'il attende moins de $3$ minutes pour voir l'étoile filante suivante est environ $0,451$. $P(T\leqslant 3) = 1-\text{e}^{-3\lambda} \approx 0,451$
- Lorsque le groupe voit une étoile filante, quelle durée minimale doit-il attendre pour voir la suivante avec une probabilité supérieure à $0,95$ ? Arrondir ce temps à la minute près. On cherche le plus petit entier naturel $t$ tel que :
- L'astronome a prévu une sortie de deux heures. Estimer le nombre moyen d'observations d'étoiles filantes lors de cette sortie. Le temps moyen d’attente entre deux étoiles filantes est $E(T)=\dfrac{1}{\lambda}=5$ minutes.
$\quad$
$\begin{align*} P(T\leqslant t) > 0,95 &\iff 1-\text{e}^{-0,2t}>0,95 \\
&\iff -\text{e}^{-0,2t}>-0,05 \\
&\iff \text{e}^{-0,2t}<0,05 \\
&\iff -0,2t<\ln 0,05 \\
&\iff t> \dfrac{\ln 0,05}{-0,2} \\
&\iff t\geqslant 15
\end{align*}$
Il faut donc que le groupe attente au minimum $15$ minutes pour après la première étoile filante pour voir la suivante avec une probabilité supérieure à $0,95$.
$\quad$
Il peut espérer voir en moyenne $\dfrac{2\times 60}{5}=24$ étoiles filantes lors de cette sortie.
$\quad$
Partie B
Ce responsable adresse un questionnaire à ses adhérents pour mieux les connaître. Il obtient les informations suivantes :
- 64% des personnes interrogées sont des nouveaux adhérents ;
- 27% des personnes interrogées sont des anciens adhérents qui possèdent un télescope personnel ;
- 65% des nouveaux adhérents n'ont pas de télescope personnel.
- On choisit un adhérent au hasard. Montrer que la probabilité que cet adhérent possède un télescope personnel est $0,494$.
- On choisit au hasard un adhérent parmi ceux qui possèdent un télescope personnel. Quelle est la probabilité que ce soit un nouvel adhérent? Arrondir à $10^{-3}$ près. On veut calculer :
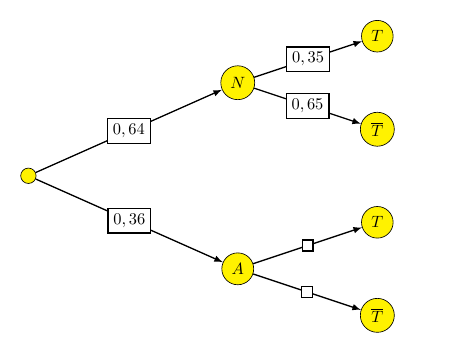 On sait que 27% des personnes interrogées sont des anciens adhérents qui possèdent un télescope personnel donc $p(A\cap T)=0,27 $
On sait que 27% des personnes interrogées sont des anciens adhérents qui possèdent un télescope personnel donc $p(A\cap T)=0,27 $D’après la formule des probabilités totales, on a :
\begin{align*} p(T)&=p(N\cap T)+p(A\cap T) \ &=0,64 \times 0,35+0,27 \\ &=0,494 \end{align*}
$p_T(N)=\dfrac{p(T\cap N)}{p(T)} =\dfrac{0,64\times 0,35}{0,494}\approx 0,453$
$\quad$
Partie C
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
Le résultat de ce sondage ne le fera donc pas changer d’avis.
$\quad$
- Vues: 33174
