Baccalauréat S Pondichéry 8 avril 2014 - Correction Exercice 4
Page 8 sur 11
Exercice 4 5 points
Le plan complexe est muni d'un repère orthonormé $\left(\text{O},\vec{u},\vec{v}\right)$. Pour tout entier naturel $n$, on note $A_{n}$ le point d'affixe $z_{n}$ défini par : \[z_{0} = 1\quad \text{et}\quad z_{n+1} = \left(\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\text{i}\right)z_{n}.\] On définit la suite $\left(r_{n}\right)$ par $r_{n} = \left|z_{n}\right|$ pour tout entier naturel $n$.
- Donner la forme exponentielle du nombre complexe $\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\text{i}$. $\left| \dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\text{i} \right|= \displaystyle\sqrt{\left(\dfrac{3}{4}\right )^2+ \left(\dfrac{\displaystyle\sqrt 3}{4}\right )^2}= \displaystyle\sqrt{\dfrac{9}{16}+\dfrac{3}{16}} = \displaystyle\sqrt{\dfrac{12}{16}} = \displaystyle\sqrt{\dfrac{3}{4}}= \dfrac{\displaystyle\sqrt 3}{2}$ $\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\text{i} = \dfrac{\displaystyle\sqrt 3}{2}\left ( \dfrac{\dfrac{3}{4}}{\dfrac{\sqrt 3}{2}} + \dfrac{\dfrac{\sqrt 3}{4}}{\dfrac{\sqrt 3}{2}}\text{i} \right ) = \dfrac{\sqrt 3}{2}\left ( \dfrac{3}{4}\times \dfrac{2}{\sqrt 3} + \dfrac{\sqrt 3}{4} \times \dfrac{2}{\sqrt 3} \text{i} \right ) = \dfrac{\sqrt 3}{2}\left ( \dfrac{\sqrt 3}{2} + \dfrac{1}{2} \text{i}\right )$ Or $\cos \dfrac{\pi}{6} = \dfrac{\sqrt 3}{2}$ et $\sin \dfrac{\pi}{6} = \dfrac{1}{2}$. Donc le nombre complexe $\dfrac{3}{4} + \dfrac{\sqrt{3}}{4}\text{i}$ a pour module $\dfrac{\sqrt 3}{2}$ et pour argument $\dfrac{\pi}{6}$ donc sa forme exponentielle est $\dfrac{\sqrt 3}{2} \,\text{e}\,^{\text{i}\frac{\pi}{6}}$.
- Montrer que la suite $\left(r_{n}\right)$ est géométrique de raison $\dfrac{\sqrt{3}}{2}$. $r_{n+1}= \left | z_{n+1} \right| = \left | \left ( \dfrac{3}{4} + \dfrac{\sqrt 3}{4}\text{i}\right ) z_n \right | = \left | \dfrac{3}{4} + \dfrac{\sqrt 3}{4}\text{i}\right | \times \left | z_n \right | = \dfrac{\sqrt 3}{2} r_n$ Donc la suite $(r_n)$ est géométrique de raison $q=\dfrac{\sqrt 3}{2}$ et de premier terme $r_0 = \left | z_0 \right | = 1$.
- En déduire l'expression de $r_{n}$ en fonction de $n$. La suite $(r_n)$ est géométrique donc, pour tout $n$, $r_n=r_0 \times q^n$, donc $r_n=\left (\dfrac{\sqrt 3}{2}\right )^n$.
- Que dire de la longueur O$A_{n}$ lorsque $n$ tend vers $+ \infty$ ? $OA_n = \left |z_n\right | = r_n = \left (\dfrac{\sqrt 3}{2}\right )^n$ $(r_n)$ est une suite géométrique de raison $\dfrac{\sqrt 3}{2}$; or $-1 < \dfrac{\sqrt 3}{2} < 1$ donc la suite $(r_n)$ converge vers 0. La longueur $OA_n$ tend donc vers 0 quand $n$ tend vers $+\infty$.
- On considère l'algorithme suivant : $$ \begin{array}{|c|c|}\hline \text{Variables}& n \text{ entier naturel }\\ &R \text{ réel }\\ &P \text{ réel strictement positif}\\ \hline \text{Entrée}& \text{Demander la valeur de } P\\ \hline \text{ Traitement }&R \text{ prend la valeur 1}\\ &n \text{ prend la valeur 0}\\ &\text{Tant que } R > P\\ & n \text{ prend la valeur } n + 1\\ & R \text{ prend la valeur } \dfrac{\sqrt{3}}{2}R\\ &\text{Fin tant que}\\ \hline \text{Sortie} & \text{Afficher } n\\ \hline \end{array} $$
- Quelle est la valeur affichée par l'algorithme pour $P = 0,5$ ? $$\begin{array}{|l| c| c|c| c|} \hline & n & R & P & R>P \\ \hline \text{Initialisations} & 0 & 1 & 0,5 & \text{Vrai}\\ \hline \text{Traitement} & 1 & 0,866 & 0,5 & \text{Vrai} \\ & 2 & 0,75 & 0,5 & \text{Vrai} \\ & 3 & 0,6495 & 0,5 & \text{Vrai}\\[-5pt] & 4 & 0,5625 & 0,5 & \text{Vrai}\\ & 5 & 0,487 & 0,5 & \text{Faux}\\ \hline \text{Sortie} & \text{Afficher }5&&& \\ \hline \end{array}$$ La valeur affichée par l'algorithme pour $P=0,5$ est 5.
- Pour $P = 0,01$ on obtient $n = 33$. Quel est le rôle de cet algorithme ? Cet algorithme s'arrête dès que $R \leq P$ et affiche alors $n$, c'est-à-dire qu'il affiche la plus petite valeur de $n$ pour laquelle $R$ donc $r_n=OA_n$ est inférieur ou égal à $P$. On peut donc dire que $OA_{32} > 0,01$ et que $OA_{33} \leq 0,01$. Vérification à la calculatrice: $r_{32}\approx 0,01002 $ et $r_{33} \approx 0,00868 $.
- Démontrer que le triangle O$A_{n}A_{n+1}$ est rectangle en $A_{n+1}$. On considère le triangle $OA_nA_{n+1}$. $OA_n=r_n$ donc $(OA_n)^2=r_n^2$ $OA_{n+1} = r_{n+1}=\dfrac{\sqrt 3}{2}r_n$ donc $(OA_{n+1})^2=\dfrac{3}{4}r_n^2$ $A_nA_{n+1}=\left | z_{n+1} - z_n \right | = \left | \left ( \dfrac{3}{4} + \dfrac{\sqrt 3}{4}\text{i} \right ) z_n -z_n \right | = \left | \left ( \dfrac{3}{4} + \dfrac{\sqrt 3}{4}\text{i} - 1 \right ) z_n \right | = \left | -\dfrac{1}{4} + \dfrac{\sqrt 3}{4}\text{i} \right | \times \left |z_n \right |$ $\phantom{A_nA_{n+1}}= \displaystyle\sqrt{ \left (-\dfrac{1}{4}\right )^2 + \left (\dfrac{\sqrt 3}{4} \right )^2} \times r_n = \displaystyle\sqrt{\dfrac{1}{16} + \dfrac{3}{16}} r_n = \displaystyle\sqrt{\dfrac{4}{16}}r_n = \dfrac{1}{2}r_n$ donc $(A_nA_{n+1})^2=\dfrac{1}{4}r_n^2$ $(A_nA_{n+1})^2+(OA_{n+1})^2 = \dfrac{1}{4}r_n^2+ \dfrac{3}{4}r_n^2 = r_n^2= (OA_n)^2$ D'après la réciproque du théorème de Pythagore, le triangle $OA_nA_{n+1}$ est rectangle en $A_{n+1}$.
- On admet que $z_{n} = r_{n}\text{e}^{\text{i}\frac{n\pi}{6}}$. Déterminer les valeurs de $n$ pour lesquelles $A_{n}$ est un point de l'axe des ordonnées. Le point $A_n$, d'affixe $z_n$, appartient à l'axe des ordonnées si et seulement si son argument est $\dfrac{\pi}{2}$ ou $\dfrac{3\pi}{2}$ modulo $2\pi$, c'est-à-dire $\dfrac{\pi}{2}$ modulo $\pi$, donc il peut s'écrire $\dfrac{\pi}{2}+k\pi$ où $k\in \mathbb{Z}$. Le nombre $z_n$ a pour argument $\dfrac{n\pi}{6}$; $\dfrac{n\pi}{6} = \dfrac{\pi}{2} + k\pi \iff n=3 +6k$. Mais $n$ est un entier naturel donc $k$ doit être strictement positif donc appartenir à $\mathbb{N}$. Donc si $n$ s'écrit $3+6k$ avec $k\in \mathbb{N}$, alors le point $A_n$ appartient à l'axe des ordonnées.
- Compléter la figure donnée en annexe, à rendre avec la copie, en représentant les points $A_{6}, A_{7}, A_{8}$ et $A_{9}$. Les traits de construction seront apparents.
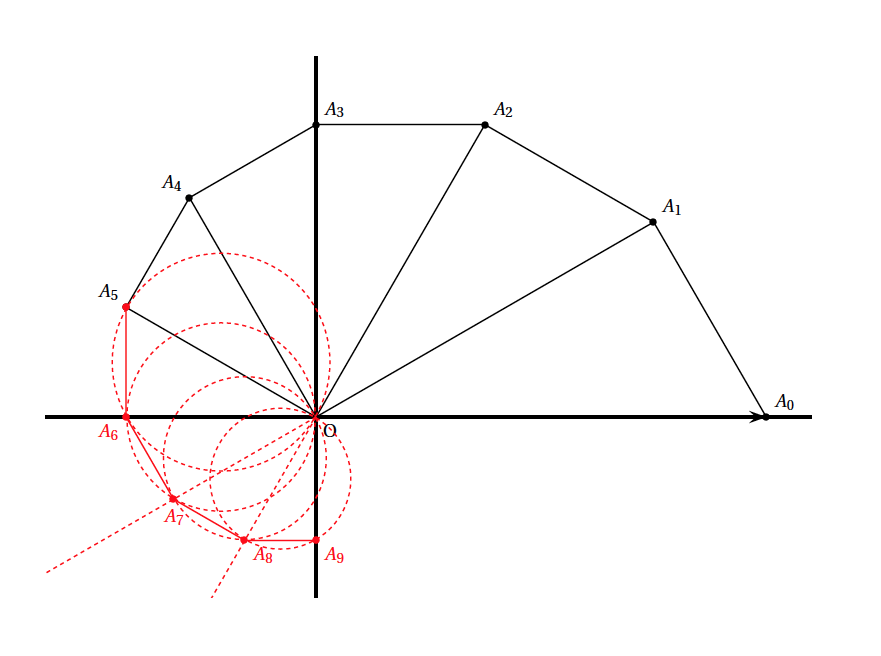
- Le point $A_6$ a pour affixe $z_6$ qui a pour argument $\dfrac{6\pi}{6} = \pi$; ce point est donc sur l'axe des abscisses. Comme le triangle $OA_5A_6$ est rectangle en $A_6$, on trace le cercle de diamètre $\texttt{[} OA_5 \texttt{]}$; le point $A_6$ est à l'intersection de ce cercle et de l'axe des abscisses. Le point $A_7$ a pour affixe $z_7$ qui a pour argument $\dfrac{7\pi}{6}$; donc les points $A_1$, $O$ et $A_7$ sont alignés. Le point $A_7$ se trouve donc à l'intersection du cercle de diamètre $\texttt{[} OA_6 \texttt{]}$ et de la droite $(OA_1)$. Etc. (Voir figure en annexe) Remarque: les points $A_3$ et $A_9$ appartiennent à l'axe des ordonnées, ce qui correspond bien à la réponse trouvée à la question \textbf{4.b.}
- Vues: 36477
