Baccalauréat S Amérique du Sud 21 novembre 2013 - Correction Exercice 2

Page 4 sur 11: Correction Exercice 2

Exercice 2 4 points

Commun à tous les candidats

On considère le cube ABCDEFGH, d'arête de longueur 1, représenté ci-dessous et on munit l'espace du repère orthonormé $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.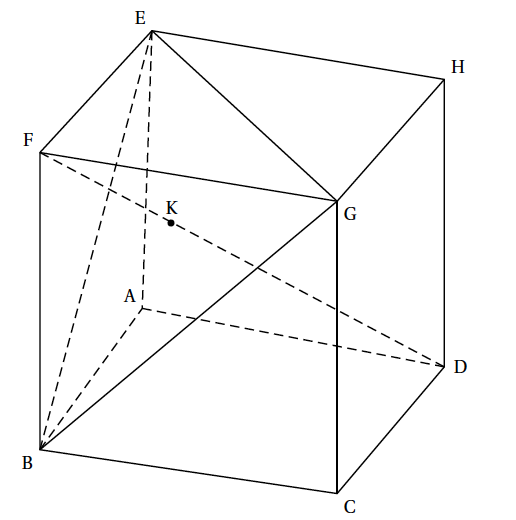

1. Déterminer une représentation paramétrique de la droite (FD).
$F(1;0;1)$ et $D(0;1;0)$ donc $\vec{FD}(-1;1;-1)$.

 

Une représentation paramétrique de $(FD)$ est donc $\left\{ \begin{array}{l} x=1-t \\\\y=t\qquad \\\\z=1-t \end{array} \right.$
1. Démontrer que le vecteur $\vec{n}\begin{pmatrix}1\\- 1\\1\end{pmatrix}$ est un vecteur normal au plan (BGE) et déterminer une équation du plan (BGE).
$B(1;0;0)$, $E(0;0;1)$ et $G(1;1;1)$

 

Donc $\vec{BG}(0;1;1)$ et $\vec{BE}(-1;0;1)$.

 

Ces $2$ vecteurs ne sont pas colinéaires.

 

$\vec{n}.\vec{BG} = 0 – 1 + 1 = 0$ et $\vec{n}.\vec{BE} = -1 + 0 + 1 = 0$.

 

Par conséquent, $\vec{n}$ est orthogonal à $2$ vecteurs non colinéaires du plan $(BGE)$.

 

Il est donc orthogonal au plan.

 

Une équation du plan $(BGE)$ est donc de la forme $x-y+z+d=0$.

 

$B$ vérifie cette équation. Par conséquent $1+d=0$ et $d=-1$.

 

Une équation cartésienne de $(BGE)$ est donc $x-y+z-1=0$.
1. Montrer que la droite (FD) est perpendiculaire au plan (BGE) en un point K de coordonnées K$\left(\frac{2}{3} ; \frac{1}{3} ; \frac{2}{3}\right)$.
$\vec{n}=-\vec{FD}$ par conséquent $\vec{FD}$ est orthogonal au plan $(BGE)$ et la droite $(FD)$ est perpendiculaire au plan $(BGE)$.

 

Recherchons les coordonnées du point d’intersection. Celles-ci vérifient le système d’équations de $(FD)$ ainsi que l’équation de $(BGE)$.

 

Donc $1-t-t+1-t-1=0$ soit $t=\dfrac{1}{3}$.

 

On obtient donc $x= \dfrac{2}{3}, y = \dfrac{1}{3}$ et $z = \dfrac{2}{3}$.

 

$K$ est donc bien le point d’intersection de $(FD)$ et de $(BGE)$.
1. Quelle est la nature du triangle BEG ? Déterminer son aire.
$[BG]$ , $[BE]$ et $[EG]$ sont des diagonales de carrés de côté $1$.

 

Par conséquent $BG = BE = EG = \sqrt{2}$. Le triangle $BEG$ est donc équilatéral.

 

Soit $I$ le milieu de $[BE]$ alors, d’après le théorème de Pythagore appliqué dans le triangle rectangle (les médianes sont aussi hauteurs, médiatrices et bissectrices dans un triangle équilatéral) $BGI$ on obtient $GI = \sqrt{\dfrac{3}{2}}$.

 

L’aire du triangle est donc $\mathcal{A} = \dfrac{BE \times GI}{2} = \dfrac{\sqrt{2} \times \sqrt{\dfrac{3}{2}}}{2} = \dfrac{\sqrt{3}}{2}$.
1. En déduire le volume du tétraèdre BEGD.
Le volume du tétraèdre est $\mathcal{V} = \dfrac{\mathcal{A} \times DK}{3}$.

 

Or $DK = \sqrt{\dfrac{4}{9} + \dfrac{4}{9} + \dfrac{4}{9}} = \dfrac{2}{\sqrt{3}}$.

 

Donc $\mathcal{V} = \dfrac{\dfrac{\sqrt{3}}{2} \times \dfrac{2}{\sqrt{3}}}{3} = \dfrac{1}{3}$