Baccalauréat S Asie 18 juin 2013 - Correction de l'Exercice 3
Page 6 sur 10
Exercice 3 4 points
Les quatre questions de cet exercice sont indépendantes.
Pour chaque question, une affirmation est proposée. Indiquer si chacune d'elles est vraie ou fausse, en justifiant la réponse. Une réponse non justifiée ne rapporte aucun point.
Dans les questions 1. et 2., le plan est rapporté au repère orthonormé direct $\left(\text{O},\vec{u},\vec{v}\right)$.
On considère les points A, B, C, D et E d'affixes respectives :
\[a = 2 + 2\text{i},\quad b = - \sqrt{3} + \text{i},\quad c = 1 + \text{i}\sqrt{3},\quad d = - 1 + \dfrac{\sqrt{3}}{2}\text{i}\quad \text{et}\quad e = - 1 + \left(2 + \sqrt{3} \right)\text{i}.\]
- Affirmation 1 : les points A, B et C sont alignés. $b-a=-\sqrt{3}+\text{i}-2-2\text{i}$ $=-2-\sqrt{3}-\text{i}$
- Affirmation 2 : les points B, C et D appartiennent à un même cercle de centre E. $|e-b|=\sqrt{8}$ $\quad |e-c|=\sqrt{8}$ $\quad |e-d| = 2+\dfrac{\sqrt{3}}{2}$
- Dans cette question, l'espace est muni d'un repère $\left(O,\vec{i},\vec{j},\vec{k}\right)$. On considère les points I(1 ; 0 ; 0), J(0 ; 1 ; 0) et K(0 ; 0 ; 1).
Affirmation 3 : la droite $\mathcal{D}$ de représentation paramétrique $\left\{\begin{array}{l c l} x &=& 2 - t \\ y &=& 6 - 2 t\\ z &=&-2 + t \end{array}\right.$ où $t \in \mathbb{R}$, coupe le plan (IJK) au point E$\left(- \dfrac{1}{2} ; 1 ; \dfrac{1}{2} \right)$. Une équation cartésienne de $(IJK)$ est de la forme $ax+by+cz+d=0$ - Dans le cube ABCDEFGH, le point T est le milieu du segment [HF].
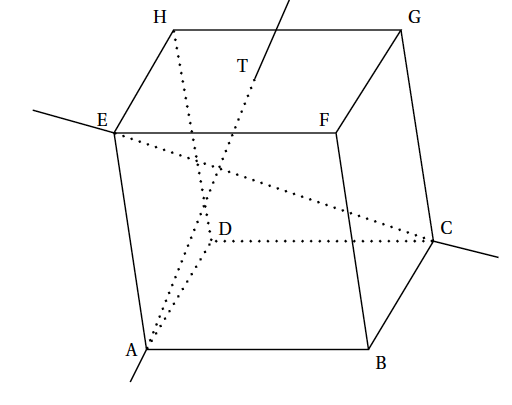
Affirmation 4 : les droites (AT) et (EC) sont orthogonales. (EFGH) est un carré donc le milieu T de [HF] est le milieu de [EG]. On a donc $\vec{ET} =\dfrac{1}{2}\vec{EG}$
$c-a=1+\text{i}\sqrt{3}-2-2\text{i}$ $=-1+\left(-2+\sqrt{3} \right)\text{i}$
Mais $\left(2+\sqrt{3}\right)(c-a) = -2-\sqrt{3} + \left(2+\sqrt{3}\right) \left(-2+\sqrt{3}\right)\text{i}$ $=-2\sqrt{3}-\text{i}=b-a$
Donc :
$$\dfrac{b-a}{c-a} = 2+\sqrt{3} \in \mathbb R$$
Les points $A$, $B$ et $C$ sont alignés.
Affirmation vraie
Affirmation fausse
$I \in (IJK)$ donc $a+d=0$. On obtient de même $b+d=0$ et $c+d=0$.
Soit $a=b=c=-d$. Prenons $d=-1$.
Une équation de $(IJK)$ est donc
$$x+y+z-1=0$$
Regardons si $E$ appartient à ce plan : $\dfrac{-1}{2}+1+\dfrac{1}{2}-1 = 0$. C’est effectivement le cas.
De plus $E \in \mathcal{D}$ (il suffit de prendre $t=\frac{5}{2}$).
Affirmation vraie
En prenant par exemple le repère $(A, \vec{AB}; \vec{AD};\vec{AE})$ calculons le produit scalaire : $\vec{AT}.\vec{EC}$ $ = \left(\vec{AE}+\dfrac{1}{2}\left(\vec{AB}+\vec{AD} \right) \right).\left(-\vec{AE}+\vec{AB}+\vec{AC} \right)$
$\vec{AT}.\vec{EC}$ $=-AE^2+\dfrac{1}{2}AB^2+\dfrac{1}{2}AD^2 = 0$
Affirmation vraie
- Vues: 44132
