Baccalauréat S Asie 18 juin 2013 - Exercice 2
Exercice 2 6 points
On considère les fonctions $f$ et $g$ définies pour tout réel $x$ par :
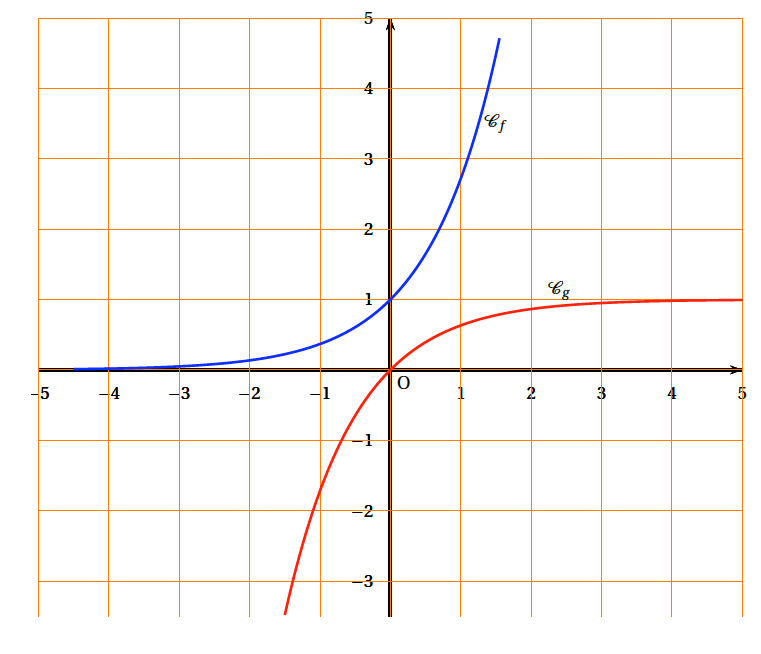
\[f(x) = \text{e}^x \quad \text{et}\quad g(x) = 1 - \text{e}^{- x}.\] Les courbes représentatives de ces fonctions dans un repère orthogonal du plan, notées respectivement $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$, sont fournies en annexe.
Partie A
Ces courbes semblent admettre deux tangentes communes. Tracer aux mieux ces tangentes sur la figure de l'annexe.
Partie B
Dans cette partie, on admet l'existence de ces tangentes communes.
On note $\mathcal{D}$ l'une d'entre elles. Cette droite est tangente à la courbe $\mathcal{C}_{f}$ au point A d'abscisse $a$ et tangente à la courbe $\mathcal{C}_{g}$ au point B d'abscisse $b$.
-
- Exprimer en fonction de $a$ le coefficient directeur de la tangente à la courbe $\mathcal{C}_{f}$ au point A.
- Exprimer en fonction de $b$ le coefficient directeur de la tangente à la courbe $\mathcal{C}_{g}$ au point B.
- En déduire que $b = - a$.
- Démontrer que le réel $a$ est solution de l'équation \[2( x - 1)\text{e}^x + 1 = 0.\]
Partie C
On considère la fonction $\varphi$ définie sur $\mathbb{R}$ par
\[\varphi(x) = 2(x -1)\text{e}^x + 1.\]
-
- Calculer les limites de la fonction $\varphi$ en $- \infty$ et $+ \infty$.
- Calculer la dérivée de la fonction $\varphi$, puis étudier son signe.
- Dresser le tableau de variation de la fonction $\varphi$ sur $\mathbb{R}$. Préciser la valeur de $\varphi(0)$.
-
- Démontrer que l'équation $\varphi(x) = 0$ admet exactement deux solutions dans $\mathbb{R}$.
- On note $\alpha$ la solution négative de l'équation $\varphi(x) = 0$ et $\beta$ la solution positive de cette équation. À l'aide d'une calculatrice, donner les valeurs de $\alpha$ et $\beta$ arrondies au centième.
Partie D
Dans cette partie, on démontre l'existence de ces tangentes communes, que l'on a admise dans la partie B. On note E le point de la courbe $\mathcal{C}_{f}$ d'abscisse $\alpha$ et F le point de la courbe $\mathcal{C}_{g}$ d'abscisse $- \alpha$ ($\alpha$ est le nombre réel défini dans la partie C).
- Démontrer que la droite (EF) est tangente à la courbe $\mathcal{C}_{f}$ au point E.
- Démontrer que (EF) est tangente à $\mathcal{C}_{g}$ au point F.
- Vues: 44362
