Baccalauréat S Métropole 21 juin 2019

Page 1 sur 10

Exercice 1 6 points

Commun à tous les candidats

 

Partie A

On considère la fonction $f$ définie sur l’ensemble $\mathbb R$ des nombres réels par : $$f(x)=\dfrac{7}{2} -\dfrac{1}{2} \left (\text{e}^{x}+\text{e}^{-x}\right )$$

1. 1. Déterminer la limite de la fonction $f$ en $+\infty$.
   2. Montrer que la fonction $f$ est strictement décroissante sur l’intervalle $[0;+\infty[$.
   3. Montrer que l’équation $f(x)=0)$ admet, sur l’intervalle $[0;+\infty[$, une unique solution, qu’on note $\alpha$.
2. En remarquant que, pour tout réel $x, f(—x) = f(x)$, justifier que l’équation $f(x) = 0$ admet exactement deux solutions dans $\mathbb R$ et qu’elles sont opposées.

Partie B

Les serres en forme de tunnel sont fréquemment utilisées pour la culture des plantes fragiles ; elles limitent les effets des intempéries ou des variations de température.
Elles sont construites à partir de plusieurs arceaux métalliques identiques qui sont ancrés au sol et supportent une bâche en plastique.
Le plan est rapporté à un repère orthonormé d’unité 1 mètre. La fonction $f$ et le réel $\alpha$ sont définis dans la partie A. Dans la suite de l’exercice, on modélise un arceau de serre par la courbe $\mathcal{C}$ de la fonction $f$ sur l’intervalle $[- \alpha;\alpha]$.
On a représenté ci-dessous la courbe $\mathcal{C}$ sur l’intervalle $[- \alpha;\alpha]$.
On admettra que la courbe admet l’axe des ordonnées pour axe de symétrie.

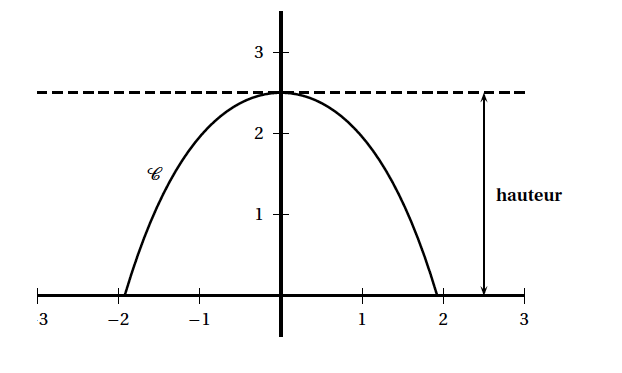
1. Calculer la hauteur d’un arceau.
2. 1. Dans cette question, on se propose de calculer la valeur exacte de la longueur de la courbe $\mathcal{C}$ sur l’intervalle $[0;\alpha]$. On admet que cette longueur est donnée, en mètre, par l’intégrale : $$I=\displaystyle\int_0^{\alpha} \sqrt{1 + \left (f'(x)\right )^2}\text{d} x.$$ Montrer que pour tout réel $x$, on a :$$1 + \left (f'(x)\right )^2=\dfrac{1}{4}\left (\text{e}^{x}+\text{e}^{-x}\right )^2$$
   2. En déduire la valeur de l’intégrale $I$ en fonction de $\alpha$.
      Justifier que la longueur d’un arceau, en mètre, est égale à :$\text{e}^{\alpha}+\text{e}^{-\alpha}$.

Partie C

On souhaite construire une serre de jardin en forme de tunnel.
On fixe au sol quatre arceaux métalliques, dont la forme est celle décrite dans la partie précédente, espacés de 1,5 mètre, comme indiqué sur le schéma ci-dessous.
Sur la façade sud, on prévoit une ouverture modélisée sur le schéma par le rectangle $ABCD$ de largeur 1 mètre et de longueur 2 mètres.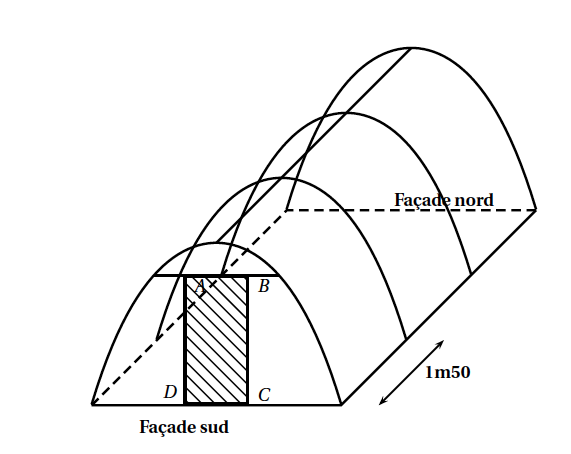

On souhaite connaître la quantité, exprimée en $m^2$, de bâche plastique nécessaire pour réaliser cette serre. Cette bâche est constituée de trois parties, l’une recouvrant la façade nord, l’autre la façade sud (sauf l’ouverture), la troisième partie de forme rectangulaire recouvrant le dessus de la serre.

1. Montrer que la quantité de bâche nécessaire pour recouvrir les façades sud et nord est donnée, en $m^2$, par :$$\mathcal{A}=\displaystyle\int_0^{\alpha} f(x)\text{d} x -2.$$
2. On prend 1,92 pour valeur approchée de $\alpha$. Déterminer, au $m^2$ près, l'aire totale de la bâche plastique nécessaire pour réaliser cette serre.