Baccalauréat S Asie 20 juin 2019
Exercice 1 6 points
La loi de refroidissement de Newton stipule que le taux d'évolution de la température d'un corps est proportionnel à la différence entre la température de ce corps et celle du milieu environnant.
Une tasse de café est servie à une température initiale de 80° dans un milieu dont la température, exprimée en degré Celsius, supposée constante, est notée $M$. Le but de cet exercice est d'étudier le refroidissement du café en appliquant la loi de Newton suivant deux modèles. L'un, dans la partie A, utilise une suite; l'autre, dans la partie B, utilise une fonction.
Les parties et B sont indépendantes
Partie A
Dans cette partie, pour tout entier naturel $n$, on note $T_n$ la température du café à l'instant $n$, avec $T_n$ exprimé en degré Celsius et $n$ en minute. On a ainsi $T_0 = 80$. On modélise la loi de Newton entre deux minutes consécutives quelconques $n$ et $n + 1$ par l'égalité: \[T_{n+1} - T_n = k\left(T_n - M\right)\] où $k$ est une constante réelle. Dans la suite de la partie A, on choisit $M = 10$ et $k = - 0,2$. Ainsi, pour tout entier naturel $n$, on a : $T_{n+1} - T_n = - 0,2 \left(T_n -10\right)$.
- D'après le contexte, peut-on conjecturer le sens de variations de la suite $\left(T_n\right)$ ?
- Montrer que pour tout entier naturel $n$ : $T_{n+1} = 0,8 T_n + 2$.
- On pose, pour tout entier naturel $n$: $u_n = T_n - 10$.
- Montrer que $\left(u_n\right)$ est une suite géométrique. Préciser sa raison et son premier terme $u_0$.
- Montrer que, pour tout entier naturel $n$, on a : $T_n = 70 \times 0,8^n + 10$.
- Déterminer la limite de la suite $\left(T_n\right)$.
- On considère l'algorithme suivant : $$\begin{array}{|c|}\hline \text{Tant que } T \geqslant 40 \\ \hspace{0.8cm} T\gets 0,8T+2 \\ \hspace{0.8cm} n \gets n+1 \\ \text{Fin Tant que }\\ \hline \end{array}$$
- Au début, on affecte la valeur $80$ à la variable $T$ et la valeur $0$ à la variable $n$. Quelle valeur numérique contient la variable $n$ à la fin de l'exécution de l'algorithme ?
- Interpréter cette valeur dans le contexte de l'exercice.
Partie B
Dans cette partie, pour tout réel $t$ positif ou nul, on note $\theta(t)$ la température du café à l'instant $t$, avec $\theta(t)$ exprimé en degré Celsius et $t$ en minute. On a ainsi $\theta(0) = 80$.
Dans ce modèle, plus précis que celui de la partie A, on suppose que $\theta$ est une fonction dérivable sur l'intervalle $[0~;~+\infty[$ et que, pour tout réel $t$ de cet intervalle, la loi de Newton se modélise par l'égalité : \[\theta'(t)= - 0,2(\theta(t) - M). \]
- Dans cette question, on choisit $M = 0$. On cherche alors une fonction $\theta$ dérivable sur l'intervalle $[0~;~+\infty[$ vérifiant $\theta(0) = 80$ et, pour tout réel $t$ de cet intervalle : $\theta'(t) = - 0,2\theta(t)$.
- Si $\theta$ est une telle fonction, on pose pour tout $t$ de l'intervalle $[0~;~+\infty[$, $f(t) = \dfrac{\theta(t)}{\text{e}^{- 0,2t}}$. Montrer que la fonction $f$ est dérivable sur $[0~;~+\infty[$ et que, pour tout réel $t$ de cet intervalle, $f'(t) = 0$.
- En conservant l'hypothèse du a. , calculer $f(0)$. En déduire, pour tout $t$ de l'intervalle $[0~;~+\infty[$ , une expression de $f(t)$, puis de $\theta(t)$.
- Vérifier que la fonction $\theta$ trouvée en b. est solution du problème.
- Dans cette question, on choisit $M = 10$. On admet qu'il existe une unique fonction $g$ dérivable sur $[0~;~+\infty[$, modélisant la température du café à tout instant positif $t$, et que, pour tout $t$ de l'intervalle $[0~;~+\infty[$ : \[g(t)=10 + 70\text{e}^{-0,2t}, \text{où } t \text{ est exprimé en minute et } g(t) \text{ en degré Celsius.} \] Une personne aime boire son café à $40$°. Montrer qu'il existe un unique réel $t_0$ dans $[0~;~+\infty[$ tel que $g\left(t_0\right) = 40$. Donner la valeur de $t_0$ arrondie à la seconde.
Correction de l'exercice 1 (6 points)
La loi de refroidissement de Newton stipule que le taux d'évolution de la température d'un corps est proportionnel à la différence entre la température de ce corps et celle du milieu environnant.
Une tasse de café est servie à une température initiale de 80° dans un milieu dont la température, exprimée en degré Celsius, supposée constante, est notée $M$. Le but de cet exercice est d'étudier le refroidissement du café en appliquant la loi de Newton suivant deux modèles. L'un, dans la partie A, utilise une suite; l'autre, dans la partie B, utilise une fonction.
Les parties et B sont indépendantes
Partie A
Dans cette partie, pour tout entier naturel $n$, on note $T_n$ la température du café à l'instant $n$, avec $T_n$ exprimé en degré Celsius et $n$ en minute. On a ainsi $T_0 = 80$. On modélise la loi de Newton entre deux minutes consécutives quelconques $n$ et $n + 1$ par l'égalité: \[T_{n+1} - T_n = k\left(T_n - M\right)\] où $k$ est une constante réelle. Dans la suite de la partie A, on choisit $M = 10$ et $k = - 0,2$. Ainsi, pour tout entier naturel $n$, on a : $T_{n+1} - T_n = - 0,2 \left(T_n -10\right)$.
- D'après le contexte, peut-on conjecturer le sens de variations de la suite $\left(T_n\right)$ ? La température du café sera toujours supérieure ou égale à celle du milieu dans lequel il est placé. Donc ici, on aura toujours $T_n\geq 10$.
- Montrer que pour tout entier naturel $n$ : $T_{n+1} = 0,8 T_n + 2$. Pour tout entier naturel $n$ on a :
- On pose, pour tout entier naturel $n$: $u_n = T_n - 10$.
- Montrer que $\left(u_n\right)$ est une suite géométrique. Préciser sa raison et son premier terme $u_0$. Pour tout entier naturel $n$ on a :
- Montrer que, pour tout entier naturel $n$, on a : $T_n = 70 \times 0,8^n + 10$. Pour tout entier naturel $n$ on a donc $u_n=70\times 0,8^n$.
- Déterminer la limite de la suite $\left(T_n\right)$. On a $-1<0,8<1$ donc $\lim\limits_{n \to +\infty} 0,8^n=0$ et $\lim\limits_{n \to +\infty}T_n=10$.
$\begin{align*} u_{n+1}&=T_{n+1}-10\\
&=0,8T_n+2-10\\
&=0,8T_n-8\\
&=0,8\left(T_n-10\right)\\
&=0,8u_n\end{align*}$
La suite $\left(u_n\right)$ est donc géométrique de raison $0,8$ et de premier terme $u_0=T_0-10=70$.
$\quad$
Donc $T_n=u_n+10=70\times 0,8^n+10$.
$\quad$
$\quad$ - On considère l'algorithme suivant : $$\begin{array}{|c|}\hline \text{Tant que } T \geqslant 40 \\ \hspace{0.8cm} T\gets 0,8T+2 \\ \hspace{0.8cm} n \gets n+1 \\ \text{Fin Tant que }\\ \hline \end{array}$$
- Au début, on affecte la valeur $80$ à la variable $T$ et la valeur $0$ à la variable $n$. Quelle valeur numérique contient la variable $n$ à la fin de l'exécution de l'algorithme ? Voici les différentes valeurs prises par les variables :
- Interpréter cette valeur dans le contexte de l'exercice. Cela signifie qu’il faut $4$ minutes pour que la température du café soit inférieure à $40$ degré Celcius.
$$\begin{array}{|c|c|c|c|c|c|}
\hline
\hspace{0.5cm}n\hspace{0.5cm}&\hspace{0.5cm}0\hspace{0.5cm}&\hspace{0.5cm}1\hspace{0.5cm}&\hspace{0.5cm}2\hspace{0.5cm}&\hspace{0.5cm}3\hspace{0.5cm}&\hspace{0.5cm}4\hspace{0.5cm}\\
\hline
T&80&66&45,84&54,8&38,672\\
\hline
\end{array}$$
À la fin de l’exécution de l’algorithme la variable $n$ contient la valeur $4$.
$\quad$
$\quad$
Ainsi $T_n-10\geq 0$.
Cela signifie donc, que pour tout entier naturel $n$ on a : $T_{n+1}-T_n=-0,2\left(T_n-10\right)\leq 0$.
On peut donc conjecturer que la suite $\left(T_n\right)$ est décroissante.
$\quad$
$\begin{align*} T_{n+1}-T_n=-0,2\left(T_n-10\right) &\iff T_{n+1}-T_n=-0,2T_n+2 \\
&\iff T_{n+1}=T_n-0,2T_n+2\\
&\iff T_{n+1}=0,8T_n+2\end{align*}$
$\quad$
Partie B
Dans cette partie, pour tout réel $t$ positif ou nul, on note $\theta(t)$ la température du café à l'instant $t$, avec $\theta(t)$ exprimé en degré Celsius et $t$ en minute. On a ainsi $\theta(0) = 80$.
Dans ce modèle, plus précis que celui de la partie A, on suppose que $\theta$ est une fonction dérivable sur l'intervalle $[0~;~+\infty[$ et que, pour tout réel $t$ de cet intervalle, la loi de Newton se modélise par l'égalité : \[\theta'(t)= - 0,2(\theta(t) - M). \]
- Dans cette question, on choisit $M = 0$. On cherche alors une fonction $\theta$ dérivable sur l'intervalle $[0~;~+\infty[$ vérifiant $\theta(0) = 80$ et, pour tout réel $t$ de cet intervalle : $\theta'(t) = - 0,2\theta(t)$.
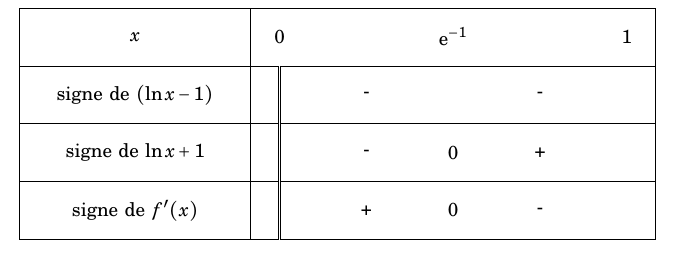
- Si $\theta$ est une telle fonction, on pose pour tout $t$ de l'intervalle $[0~;~+\infty[$, $f(t) = \dfrac{\theta(t)}{\text{e}^{- 0,2t}}$. Montrer que la fonction $f$ est dérivable sur $[0~;~+\infty[$ et que, pour tout réel $t$ de cet intervalle, $f'(t) = 0$. La fonction $t\mapsto -0,2t$ est dérivable sur l’intervalle $[0;+\infty[$ et la fonction exponentielle est dérivable sur $\mathbb R$. La fonction $t\mapsto \text{e}^{-0,2t}$ est donc dérivable sur l’intervalle $[0;+\infty[$.
- En conservant l'hypothèse du a. , calculer $f(0)$. En déduire, pour tout $t$ de l'intervalle $[0~;~+\infty[$ , une expression de $f(t)$, puis de $\theta(t)$. On a $f(0)=\dfrac{\theta(0)}{\text{e}^0}=80$.
- Vérifier que la fonction $\theta$ trouvée en b. est solution du problème. On considère la fonction $\theta$ définie sur l’intervalle $[0;+\infty[$ par $\theta(t)=80\text{e}^{-0,2t}$.
La fonction $f$ est dérivable sur l’intervalle $[0;+\infty[$ en tant que quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas (la fonction exponentielle est strictement positive sur $\mathbb R$).
$\quad$
Pour tout réel $t\geq 0$ on a :
$\begin{align*} f'(t)&=\dfrac{\theta'(t)\times \text{e}^{-0,2t}-\theta(t)\times \left(-0,2\text{e}^{-0,2t}\right)}{\text{e}^{-0,4t}}\\
&=\dfrac{\left(\theta'(t)+0,2\theta(t)\right)\text{e}^{-0,2t}}{\text{e}^{-0,4t}}\\
&=\dfrac{-0,2\theta(t)+0,2\theta(t)}{\text{e}^{-0,2t}}\\
&=0\end{align*}$
$\quad$
D’après la question 1.a. la fonction $f$ est donc constante.
Et pour tout réel $t\geq 0$ on a $f(t)=80$.
Cela signifie donc que : $$80=\dfrac{\theta(t)}{\text{e}^{-0,2t}} \iff \theta(t)=80\text{e}^{-0,2t}$$
$\quad$
Ainsi $\theta(0)=80$.
La fonction $\theta$ est dérivable sur l’intervalle $[0;+\infty[$ en tant que produit d’une fonction dérivable sur cet intervalle par un réel.
De plus, pour tout réel $t \geq 0$ on a :
$\theta'(t)=80\times \left(-0,2\text{e}^{-0,2t}\right)=-0,2\theta(t)$.
La fonction $\theta$ est donc solution du problème.
$\quad$ - Dans cette question, on choisit $M = 10$. On admet qu'il existe une unique fonction $g$ dérivable sur $[0~;~+\infty[$, modélisant la température du café à tout instant positif $t$, et que, pour tout $t$ de l'intervalle $[0~;~+\infty[$ : \[g(t)=10 + 70\text{e}^{-0,2t}, \text{où } t \text{ est exprimé en minute et } g(t) \text{ en degré Celsius.} \] Une personne aime boire son café à $40$°. Montrer qu'il existe un unique réel $t_0$ dans $[0~;~+\infty[$ tel que $g\left(t_0\right) = 40$. Donner la valeur de $t_0$ arrondie à la seconde. D’après l’énoncé, la fonction $g$ est dérivable sur l’intervalle $[0;+\infty[$.
Pour tout réel $t\geq 0$ on a $g'(t)=70\times \left(-0,2\text{e}^{-0,2t}\right)=-14\text{e}^{-0,2t}$.
La fonction exponentielle étant strictement positive sur $\mathbb R$, cela signifie donc que $g'(t)<0$.
La fonction $g$ est donc décroissante sur $[0;+\infty[$. Elle est de plus continue (car dérivable) sur cet intervalle.
$g(0)=80$
$\lim\limits_{t\to +\infty} -0,2t=-\infty$ et $\lim\limits_{T \to -\infty}\text{e}^{T}=0$ donc $\lim\limits_{t\to +\infty} \text{e}^{-0,2t}=0$ et $\lim\limits_{t\to +\infty} g(t)=10$.
Or $40\in]10;80]$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $g(t)=40$ possède une unique solution $t_0$.
D’après la calculatrice $t_0\approx 4,236$.
$0,436$ min $\approx 26$ s.
Ainsi $t_0 \approx 4$ min $26$ s.
$\quad$
Exercice 2 5 points
Pour chacune des questions suivantes, une seule des quatre affirmations est exacte. Indiquer sur la copie le numéro de la question et recopier la lettre correspondant à l'affirmation exacte. Il est attribué un point si la lettre correspond à l'affirmation exacte, $0$ sinon.
Dans tout l'exercice, on se place dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ de l'espace.
Les quatre questions sont indépendantes.
Aucune justification n'est demandée.
- On considère le plan P d' équation cartésienne $3x + 2 y + 9 z - 5 = 0$ et la droite $d$ dont une représentation paramétrique est: $\left\{\begin{array}{l c l} x &= &4t+3\\ y& =& - t + 2 \\z&=& -t+9 \end{array}\right. , t \in \mathbb R$.
- l'intersection du plan $P$ et de la droite $d$ est réduite au point de coordonnées $(3~;~2~;~9)$.
- le plan $P$ et la droite $d$ sont orthogonaux.
- le plan $P$ et la droite $d$ sont parallèles.
- l'intersection du plan $P$ et de la droite $d$ est réduite au point de coordonnées $(-353~;~91~;~98)$.
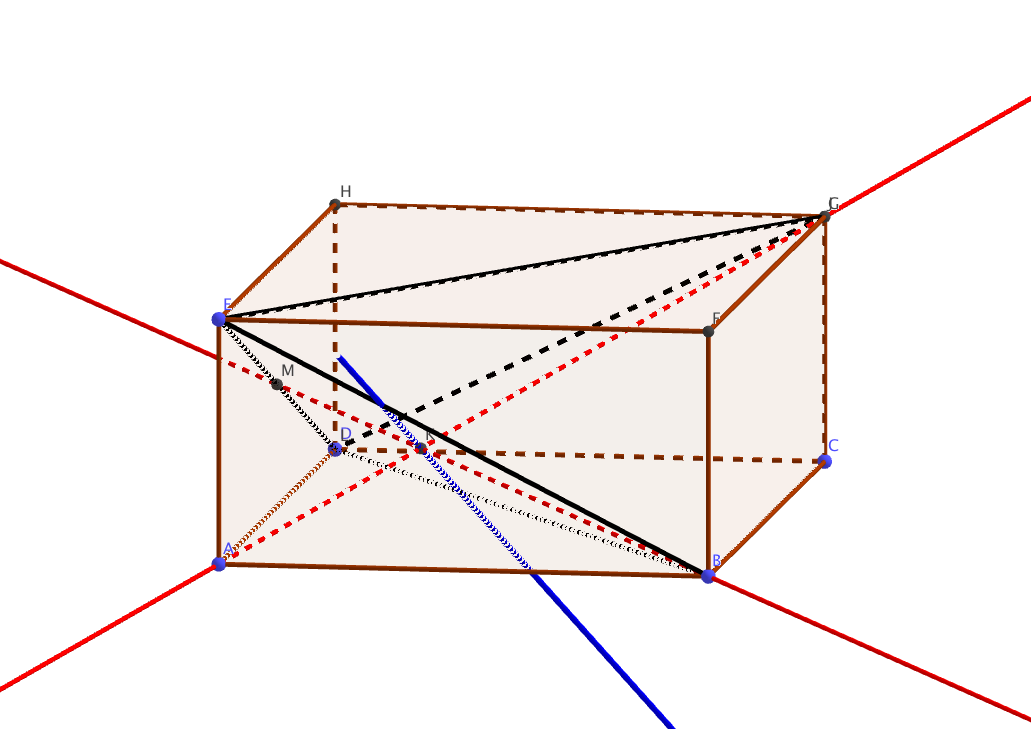
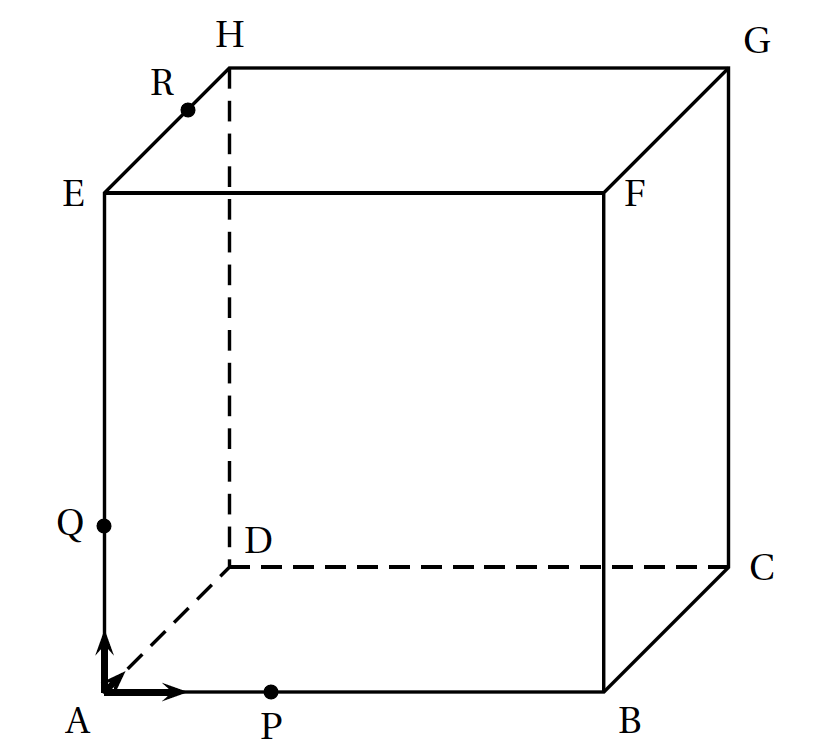
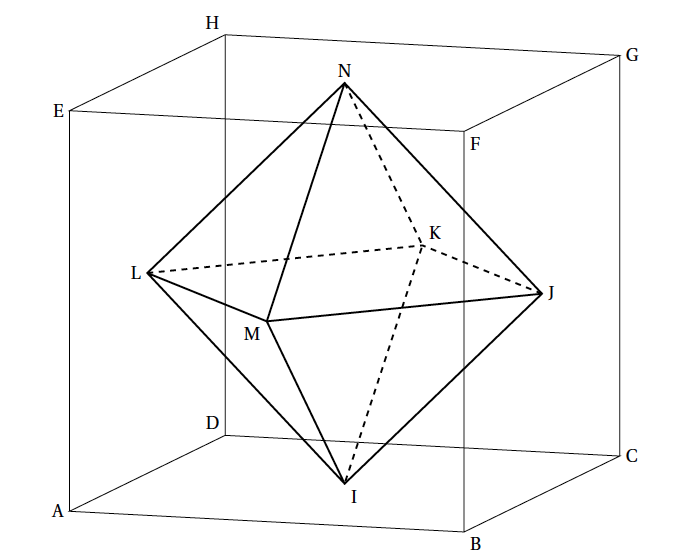
- On considère le cube ABCDEFGH représenté ci-dessous et les points I, J et K définis par les égalités vectorielles :
$\vec{AI}=\dfrac{3}{4}\vec{AB}$, $\vec{DJ}=\dfrac{1}{4}\vec{DC}$ et $\vec{HK}=\dfrac{3}{4}\vec{HG}$
- la section du cube ABCDEFGH par le plan (UK) est un triangle.
- la section du cube ABCDEFGH par le plan (UK) est un quadrilatère.
- la section du cube ABCDEFGH par le plan (UK) est un pentagone.
- la section du cube ABCDEFGH par le plan (UK) est un hexagone.
- On considère la droite $d$ dont une représentation paramétrique est $\left\{\begin{array}{l c r} x&=&t + 2\\y &=& 2\\z&=&5t - 6 \end{array}\right.$ , avec $t \in \mathbb R$, et le point A$( - 2~;~1~;~0)$. Soit $M$ un point variable de la droite $d$.
- la plus petite longueur A$M$ est égale à $\sqrt{53}$ .
- la plus petite longueur A$M$ est égale à $\sqrt{27}$.
- la plus petite longueur A$M$ est atteinte lorsque le point M a pour coordonnées $(-2~;~1~;~0)$.
- la plus petite longueur A$M$ est atteinte lorsque le point $M$ a pour coordonnées $(2~;~2~;~-6)$.
- On considère le plan $P$ d'équation cartésienne $x+2y-3z+1=0$ et le plan $P'$ d'équation cartésienne $2x - y + 2 = 0$.
- les plans $P$ et $P'$ sont parallèles.
- l'intersection des plans $P$ et $P'$ est une droite passant par les points A$(5~;~12~;~10)$ et B $(3~;~1~;~2)$.
- l'intersection des plans $P$ et $P'$ est une droite passant par le point C$(2~;~6~;~5)$ et dont un vecteur directeur est $\vec{u}(1~;~2~;~2)$.
- l'intersection des plans $P$ et $P'$ est une droite passant par le point D$(-1~;~0~;~0)$ et dont un vecteur directeur est $\vec{v}(3~;~6~;~5)$.
Correction de l'exercice 2 (4 points)
Pour chacune des questions suivantes, une seule des quatre affirmations est exacte. Indiquer sur la copie le numéro de la question et recopier la lettre correspondant à l'affirmation exacte. Il est attribué un point si la lettre correspond à l'affirmation exacte, $0$ sinon.
Dans tout l'exercice, on se place dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ de l'espace.
Les quatre questions sont indépendantes.
Aucune justification n'est demandée.
- On considère le plan P d' équation cartésienne $3x + 2 y + 9 z - 5 = 0$ et la droite $d$ dont une représentation paramétrique est: $\left\{\begin{array}{l c l} x &= &4t+3\\ y& =& - t + 2 \\z&=& -t+9 \end{array}\right. , t \in \mathbb R$.
- l'intersection du plan $P$ et de la droite $d$ est réduite au point de coordonnées $(3~;~2~;~9)$.
- le plan $P$ et la droite $d$ sont orthogonaux.
- le plan $P$ et la droite $d$ sont parallèles.
- l'intersection du plan $P$ et de la droite $d$ est réduite au point de coordonnées $(-353~;~91~;~98)$.
-
On constate que les coordonnées fournies dans l’affirmation A ne vérifie par l’équation cartésienne du plan P .
Les vecteur $\vec{n}(3;2;9)$, normal au plan $p$, et $\vec{u}(4;-1;-1)$, vecteur directeur de la droite $d$, ne sont ni orthogonaux (produit scalaire non nul) ni colinéaires. Les affirmations B et C sont donc fausse.
$3\times (-353)+2\times 91+9\times 98-5=0$. Le point $A(-353;91;98)$ appartient au plan $p$.
En prenant $t=-89$ (il suffit de résoudre l’équation $-t+9=98$) on constate que le point $A$ appartient également à la droite $d$. Affirmation d vraie - On considère le cube ABCDEFGH représenté ci-dessous et les points I, J et K définis par les égalités vectorielles :
$\vec{AI}=\dfrac{3}{4}\vec{AB}$, $\vec{DJ}=\dfrac{1}{4}\vec{DC}$ et $\vec{HK}=\dfrac{3}{4}\vec{HG}$
- la section du cube ABCDEFGH par le plan (UK) est un triangle.
- la section du cube ABCDEFGH par le plan (UK) est un quadrilatère.
- la section du cube ABCDEFGH par le plan (UK) est un pentagone.
- la section du cube ABCDEFGH par le plan (UK) est un hexagone.
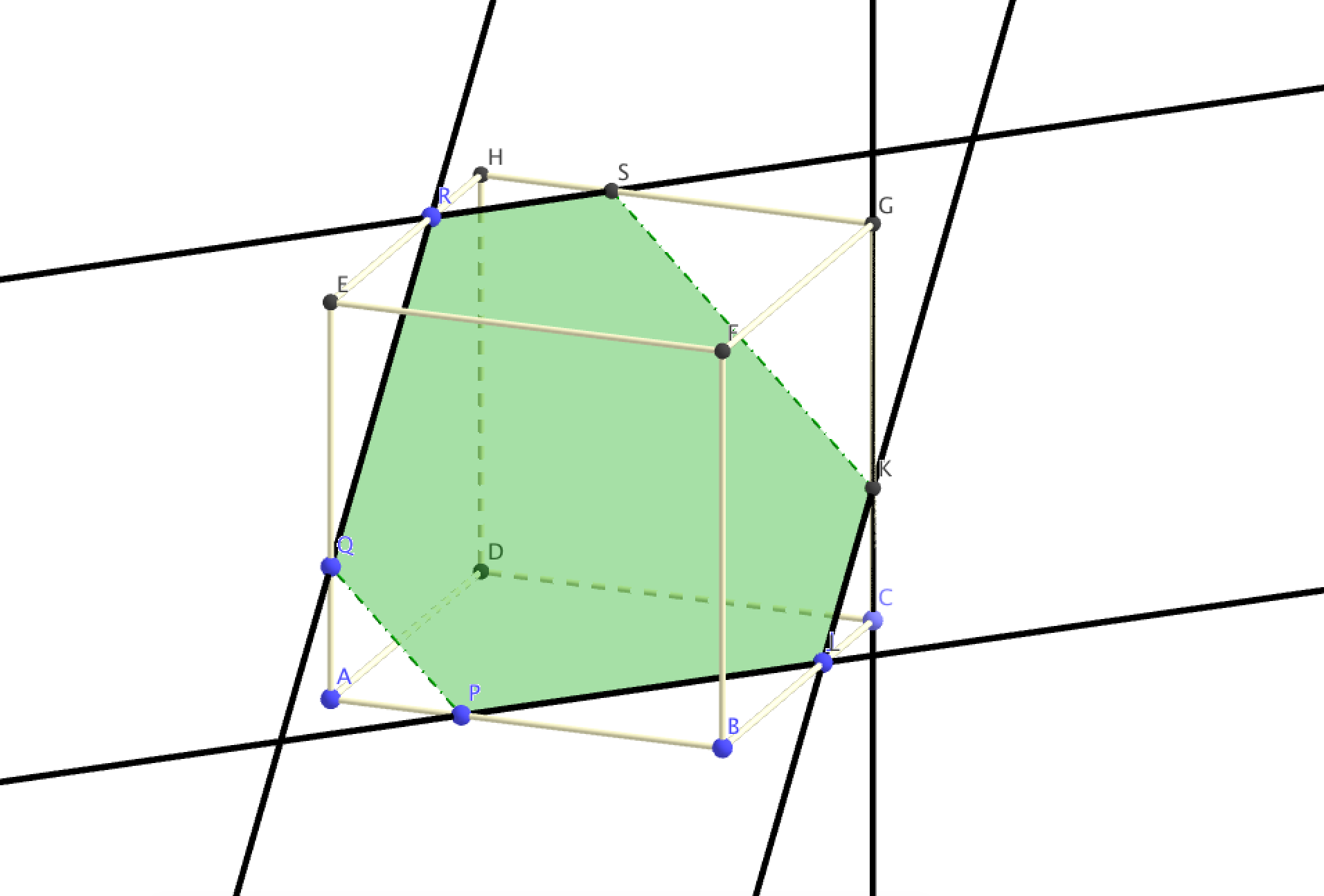
On obtient la figure suivante : - On considère la droite $d$ dont une représentation paramétrique est $\left\{\begin{array}{l c r} x&=&t + 2\\y &=& 2\\z&=&5t - 6 \end{array}\right.$ , avec $t \in \mathbb R$, et le point A$( - 2~;~1~;~0)$. Soit $M$ un point variable de la droite $d$.
- la plus petite longueur A$M$ est égale à $\sqrt{53}$ .
- la plus petite longueur A$M$ est égale à $\sqrt{27}$.
- la plus petite longueur A$M$ est atteinte lorsque le point M a pour coordonnées $(-2~;~1~;~0)$.
- la plus petite longueur A$M$ est atteinte lorsque le point $M$ a pour coordonnées $(2~;~2~;~-6)$.
On a : - On considère le plan $P$ d'équation cartésienne $x+2y-3z+1=0$ et le plan $P'$ d'équation cartésienne $2x - y + 2 = 0$.
- les plans $P$ et $P'$ sont parallèles.
- l'intersection des plans $P$ et $P'$ est une droite passant par les points A$(5~;~12~;~10)$ et B $(3~;~1~;~2)$.
- l'intersection des plans $P$ et $P'$ est une droite passant par le point C$(2~;~6~;~5)$ et dont un vecteur directeur est $\vec{u}(1~;~2~;~2)$.
- l'intersection des plans $P$ et $P'$ est une droite passant par le point D$(-1~;~0~;~0)$ et dont un vecteur directeur est $\vec{v}(3~;~6~;~5)$.
-
$\vec{n}(1;2;-3)$ est un vecteur normal au plan $p$ et $\vec{n’}(2;-1;0)$ est un vecteur normal au plan P.
Ces deux vecteurs ne sont pas colinéaires. Affirmation a fausse.
Le point $B$ ne vérifie pas l’équation cartésienne du plan $p’$. Affirmation b fausse.
$\vec{n}.\vec{u}=-1\neq 0$. Aucune droite de vecteur directeur $\vec{u}$ n’est incluse dans le plan P.
$\vec{n}.\vec{u}=0$ et $\vec{n’}.\vec{u}=0$. De plus les coordonnées du point $D$ vérifient les deux équations cartésiennes. Affirmation d vraie
$\quad$

Affirmation c vraie
$\quad$
$\begin{align*} AM^2&=(t+2+2)^2+(2-1)^2+(5t-6)^2 \\
&=(t+4)^2+1+(5t-6)^2\\
&=t^2+8t+16+1+25t^2-60t+36\\
&=26t^2-52t+53\end{align*}$
$a=26>0$ : le polynôme du second degré atteint donc son minimum pour $t=-\dfrac{-52}{2\times 26}=1$.
Ce minimum vaut $27$.
Ainsi la plus petite longueur $AM$ est égale à $\sqrt{27}$.
Affirmation b vraie
$\quad$
$\quad$
Exercice 3 5 points
Les parties A, B et C sont indépendantes. Dans tout l'exercice, on arrondira les résultats au millième.
Partie A
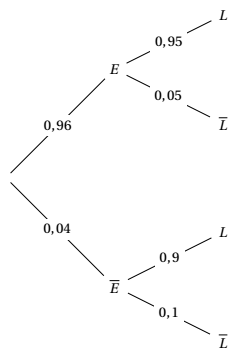
En France, la consommation de produits bio croît depuis plusieurs années. En 2017, le pays comptait 52$\:\%$ de femmes. Cette même année, 92$\:\%$ des Français avaient déjà consommé des produits bio. De plus, parmi les consommateurs de produits bio, 55$\:\%$ étaient des femmes. On choisit au hasard une personne dans le fichier des Français de 2017. On note :
- $F$ l'évènement « la personne choisie est une femme » ;
- $H$ l'évènement « la personne choisie est un homme» ;
- $B$ l'évènement « la personne choisie a déjà consommé des produits bio » .
- Traduire les données numériques de l'énoncé à l'aide des évènements $F$ et $B$.
-
- Montrer que $P(F \cap B) = 0,506$.
- En déduire la probabilité qu'une personne ait consommé des produits bio en 2017, sachant que c'est une femme.
- Calculer $P_H\left(\overline{B}\right)$. Interpréter ce résultat dans le contexte de l'exercice.
Partie B
Dans un supermarché, un chef de rayon souhaite développer l'offre de produits bio. Afin de justifier sa démarche, il affirme à son responsable que 75% des clients achètent des produits bio au moins une fois par mois. Le responsable souhaite vérifier ses dires. Pour cela, il organise un sondage à la sortie du magasin. Sur 2000 personnes interrogées, 1421 répondent qu'elles consomment des produits bio au moins une fois par mois. Au seuil de 95% que peut-on penser de l'affirmation du chef de rayon ?
Partie C
Pour promouvoir les produits bio de son enseigne, le responsable d'un magasin décide d'organiser un jeu qui consiste, pour un client, à remplir un panier avec une certaine masse d'abricots issus de l'agriculture biologique. Il est annoncé que le client gagne le contenu du panier si la masse d'abricots déposés est comprise entre $3,2$ et $3,5$ kilogrammes. La masse de fruits en kg, mis dans le panier par les clients, peut être modélisée par une variable aléatoire $X$ suivant la loi de probabilité de densité $f$ définie sur l'intervalle [3 ; 4] par : \[f(x) = \dfrac{2}{(x - 2)^2}.\] Rappel : on appelle fonction de densité d'une loi de probabilité sur l'intervalle $[a~;~b]$ toute fonction $f$ définie, continue et positive sur $[a~;~b]$, telle que l'intégrale de $f$ sur $[a~;~b]$ est égale à 1.
- Vérifier que la fonction $f$ précédemment définie est bien une fonction de densité d'une loi de probabilité sur l'intervalle $[3~;~4]$.
- Le magasin annonce : « Un client sur trois gagne le panier ! » . Cette annonce est-elle exacte ?
- Cette question a pour but de calculer l'espérance mathématique E($X$) de la variable aléatoire $X$. On rappelle que, pour une variable aléatoire $X$ de densité $f$ sur l'intervalle $[a~;~b]$,\: E($X$) est donnée par : $$E (X) = \displaystyle\int_a^b x f(x)\:\text{d}x.$$
- Vérifier que la fonction $G$, définie sur l'intervalle $[3~;~4]$ par $G(x) = \ln (x - 2) - \dfrac{x}{x - 2}$, est une primitive de la fonction $x \longmapsto \dfrac{x}{(x - 2)^2}$ sur cet intervalle.
- En déduire la valeur exacte de E($X$), puis sa valeur arrondie au centième. Interpréter le résultat dans le contexte de l'exercice.
Correction de l'exercice 3 (5 points)
Les parties A, B et C sont indépendantes. Dans tout l'exercice, on arrondira les résultats au millième.
Partie A
En France, la consommation de produits bio croît depuis plusieurs années. En 2017, le pays comptait 52$\:\%$ de femmes. Cette même année, 92$\:\%$ des Français avaient déjà consommé des produits bio. De plus, parmi les consommateurs de produits bio, 55$\:\%$ étaient des femmes. On choisit au hasard une personne dans le fichier des Français de 2017. On note :
- $F$ l'évènement « la personne choisie est une femme » ;
- $H$ l'évènement « la personne choisie est un homme» ;
- $B$ l'évènement « la personne choisie a déjà consommé des produits bio » .
- Traduire les données numériques de l'énoncé à l'aide des évènements $F$ et $B$. On a $P(F)=0,52$, $P(B)=0,92$ et $P_B(F)=0,55$.
-
- Montrer que $P(F \cap B) = 0,506$. On a :
- En déduire la probabilité qu'une personne ait consommé des produits bio en 2017, sachant que c'est une femme. On veut calculer :
$\begin{align*}P(F\cap B)&=P_B(F)\times P(B)\\
&=0,55\times 0,92\\
&=0,506\end{align*}$
$\quad$
$\begin{align*} P_F(B)&=\dfrac{P(F\cap B)}{P(F)} \\
&=\dfrac{0,506}{0,52} \\
&\approx 0,973\end{align*}$
La probabilité qu’une personne ait consommé des produits bio en 2017, sachant que c’est une femme, est environ égale à $0,973$.
$\quad$ - Calculer $P_H\left(\overline{B}\right)$. Interpréter ce résultat dans le contexte de l'exercice. On a : $P\left(\overline{B}\right)=1-P(B)=0,08$.
$\quad$
De plus $P_F(B)=0,973$ donc $P_F\left(\overline{B}\right)=0,027$
Par conséquent $P\left(F\cap \overline{B}\right)=0,027\times 0,52=0,014~04$
D’après la formule des probabilités totales on a :
$\begin{align*} & P\left(\overline{B}\right)=P\left(H\cap \overline{B}\right)+P\left(F\cap \overline{B}\right) \\
\iff & 0,08=P\left(H\cap \overline{B}\right)+0,014~04\\
\iff & P\left(H\cap \overline{B}\right)=0,065~96\end{align*}$
Ainsi :
$\begin{align*} P_H\left(\overline{B}\right)&=\dfrac{P\left(H\cap \overline{B}\right)}{P(H)} \\
&=\dfrac{0,065~96}{1-0,52}\\
&\approx 0,137\end{align*}$
La probabilité qu’une personne n’ait jamais consommé des produits bio en 2017, sachant que c’est un homme, est environ égale à $0,137$.
$\quad$
Partie B
On a $n=2~000$ et $p=0,75$.
Par conséquent $n\geq 30$, $np=1~500\geq 5$ et $n(1-p)=500\geq 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion de personne consommant des produits bio au moins une fois par mois est :
$\begin{align*} I_{2~000}&=\left[0,75-1,96\sqrt{\dfrac{0,75\times 0,25}{2~000}};0,75+1,96\sqrt{\dfrac{0,75\times 0,25}{2~000}}\right]\\
&\approx [0,731;0,769]\end{align*}$
La fréquence observée est $f=\dfrac{1~421}{2~000}=0,710~5\notin I_{2~000}$.
Au risque d’erreur de $5\%$ on peut dire que l’affirmation du chef de rayon est fausse.
$\quad$
Partie C
Pour promouvoir les produits bio de son enseigne, le responsable d'un magasin décide d'organiser un jeu qui consiste, pour un client, à remplir un panier avec une certaine masse d'abricots issus de l'agriculture biologique. Il est annoncé que le client gagne le contenu du panier si la masse d'abricots déposés est comprise entre $3,2$ et $3,5$ kilogrammes. La masse de fruits en kg, mis dans le panier par les clients, peut être modélisée par une variable aléatoire $X$ suivant la loi de probabilité de densité $f$ définie sur l'intervalle [3 ; 4] par : \[f(x) = \dfrac{2}{(x - 2)^2}.\] Rappel : on appelle fonction de densité d'une loi de probabilité sur l'intervalle $[a~;~b]$ toute fonction $f$ définie, continue et positive sur $[a~;~b]$, telle que l'intégrale de $f$ sur $[a~;~b]$ est égale à 1.
- Vérifier que la fonction $f$ précédemment définie est bien une fonction de densité d'une loi de probabilité sur l'intervalle $[3~;~4]$. La fonction $f$ est définie sur l’intervalle $[3;4]$. Elle est également continue sur cet intervalle en tant que quotient de fonctions continues sur $[3;4]$ dont le dénominateur ne s’annule pas.
- Le magasin annonce : « Un client sur trois gagne le panier ! » . Cette annonce est-elle exacte ? On a :
- Cette question a pour but de calculer l'espérance mathématique E($X$) de la variable aléatoire $X$. On rappelle que, pour une variable aléatoire $X$ de densité $f$ sur l'intervalle $[a~;~b]$,\: E($X$) est donnée par : $$E (X) = \displaystyle\int_a^b x f(x)\:\text{d}x.$$
- Vérifier que la fonction $G$, définie sur l'intervalle $[3~;~4]$ par $G(x) = \ln (x - 2) - \dfrac{x}{x - 2}$, est une primitive de la fonction $x \longmapsto \dfrac{x}{(x - 2)^2}$ sur cet intervalle. La fonction $G$ est dérivable sur l’intervalle $[3;4]$ en tant que somme et quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
- En déduire la valeur exacte de E($X$), puis sa valeur arrondie au centième. Interpréter le résultat dans le contexte de l'exercice. Ainsi :
Pour tout réel $x$ appartenant à l’intervalle $[3;4]$ on a :
$\begin{align*} G'(x)&=\dfrac{1}{x-2}-\dfrac{1\times (x-2)-x\times 1}{(x-2)^2}\\
&=\dfrac{1}{x-2}+\dfrac{2}{(x-2)^2} \\
&=\dfrac{x-2+2}{(x-2)^2}\\
&=\dfrac{x}{(x-2)^2}\\
&=g(x)\end{align*}$
La fonction $G$ est donc une primitive de la fonction $g$ sur l’intervalle $[3;4]$.
$\quad$
$\begin{align*} E(X)&=\int_3^4xf(x)\text{d} x \\
&=2\int_3^4g(x)\text{d} x \\
&=2\left(G(4)-G(3)\right)\\
&=2\left(\ln(2)-2-\left(\ln(1)-3\right)\right)\\
&=2\left(\ln(2)+1\right)\\
&\approx 3,39\end{align*}$
En moyenne le contenu du panier déposé par les clients a une masse d’abricots environ égale à $3,39$ kg.
$\quad$
La fonction carré est positive sur $\mathbb R$. Par conséquent, pour tout réel $x\in[2;3]$ on a $f(x)\geq 0$.
$\begin{align*} I&=\displaystyle \int_3^4 f(x)\text{d} x \\
&=2\left[-\dfrac{1}{x-2}\right]_3^4\\
&=2\left(-\dfrac{1}{2}+1\right)\\
&=1\end{align*}$
La fonction $f$ est une fonction de densité d’une loi de probabilité sut l’intervalle $[3;4]$.
$\quad$
$\begin{align*} P(3,2\leq X\leq 3,5)&=\displaystyle \int_{3,2}^{3,5}f(x)\text{d} x \\
&=2\left[-\dfrac{1}{x-2}\right]_{3,2}^{3,5}\\
&=2\left(-\dfrac{2}{3}+\dfrac{5}{6}\right)\\
&=\dfrac{1}{3}\end{align*}$
L’annonce est donc exacte.
$\quad$
Exercice 4 5 points
- On considère dans l'ensemble des nombres complexes l'équation $(E)$ à l'inconnue $z$ : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = 0\quad (E). \]
- Montrer que le nombre $-2\text{i}$ est une solution de l'équation $(E)$.
- Vérifier que, pour tout nombre complexe $z$, on a : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = (z + 2i)\left(z^2 - 2\sqrt{3} z + 4\right).\]
- Résoudre l'équation $(E)$ dans l'ensemble des nombres complexes.
- Écrire les solutions de l'équation $(E)$ sous forme exponentielle.
Dans la suite, on se place dans le plan muni d'un repère orthonormé direct d'origine $O$.
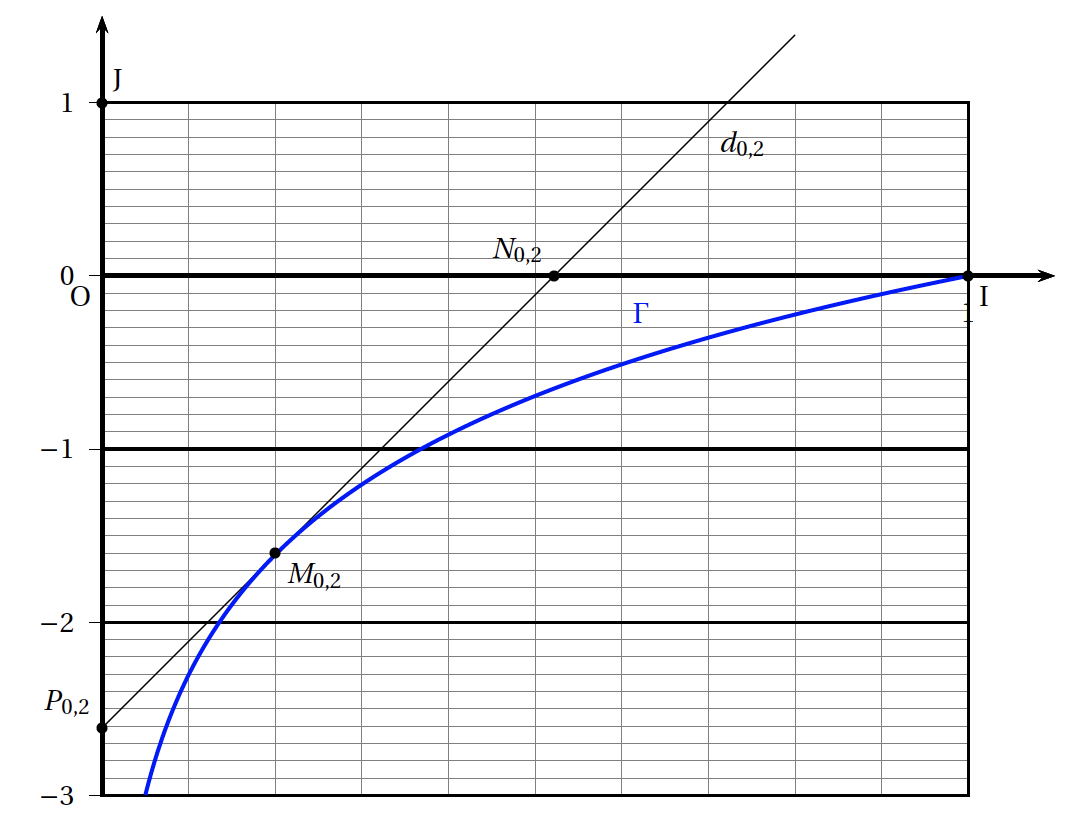
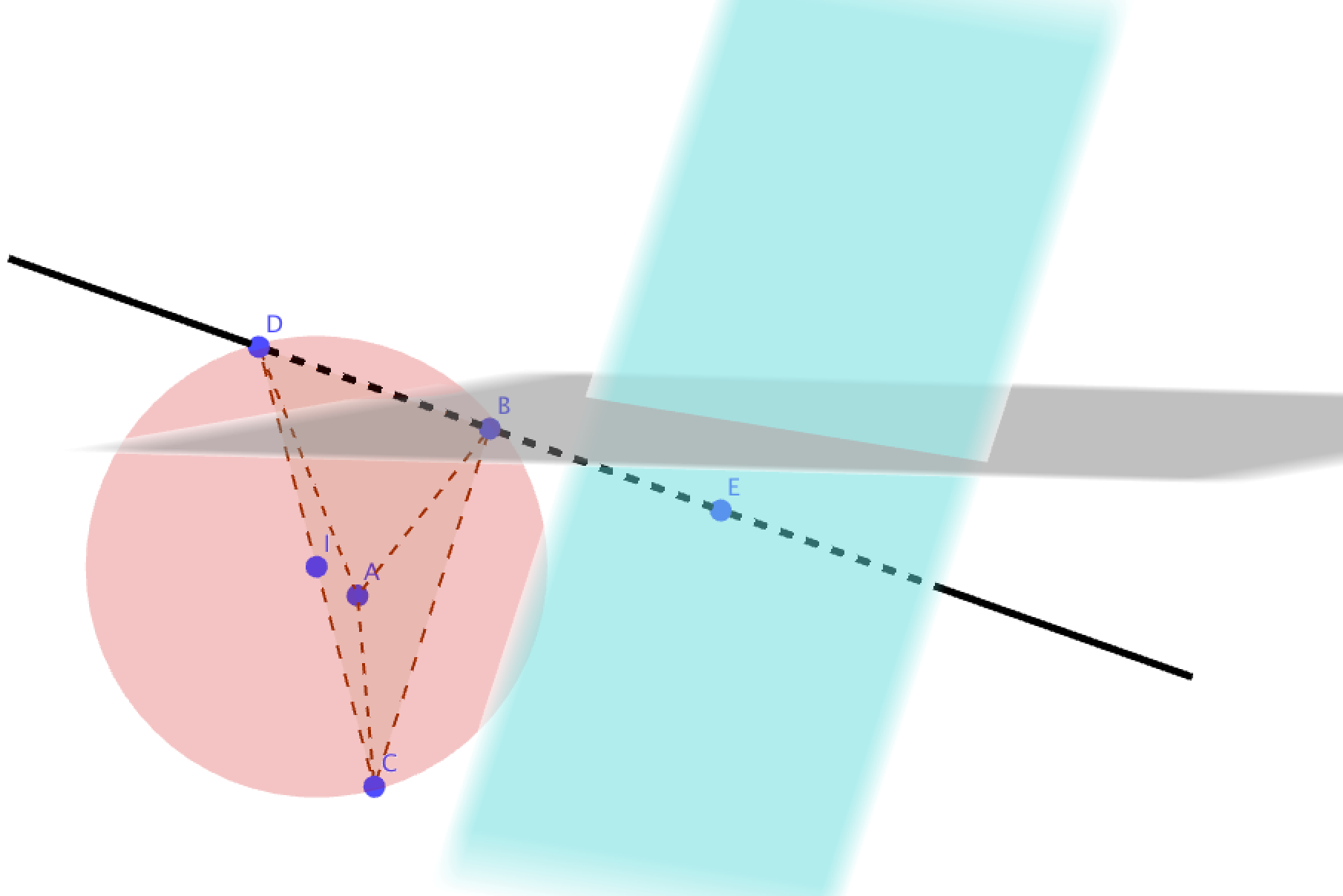
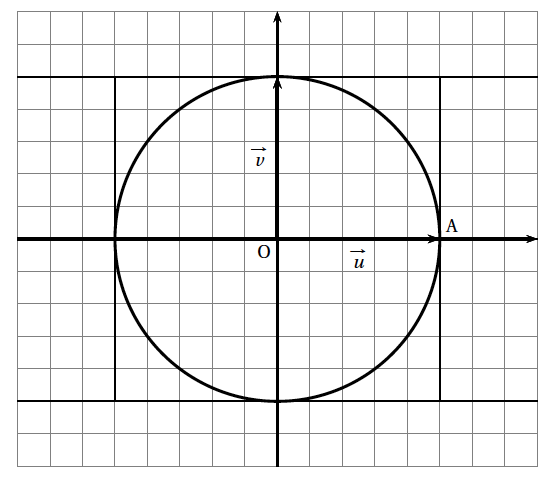
- On considère les points A, B, C d'affixes respectives $-2i$, $\sqrt{3} + \text{i}$ et $\sqrt{3} - \text{i}$.
- Montrer que A, B et C appartiennent à un même cercle de centre O dont on déterminera le rayon.
- Placer ces points sur une figure que l'on complètera par la suite.
- On note D le milieu du segment [OB]. Déterminer l'affixe $z_{\text{L}}$ du point L tel que AODL soit un parallélogramme.
- On rappelle que, dans un repère orthonormé du plan, deux vecteurs de coordonnées respectives $(x~;~y)$ et $(x'~;~y')$ sont orthogonaux si et seulement si $xx'+yy' = 0$.
- Soit $\vec{u}$ et $\vec{v}$ deux vecteurs du plan, d'affixes respectives $z$ et $z'$. Montrer que $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si $z \overline{z'}$ est un imaginaire pur.
- À l'aide de la question \textbf{3. a.}, démontrer que le triangle AOL est rectangle en L.
Correction de l'exercice 4 5 points
- On considère dans l'ensemble des nombres complexes l'équation $(E)$ à l'inconnue $z$ : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = 0\quad (E). \]
- Montrer que le nombre $-2\text{i}$ est une solution de l'équation $(E)$. $\begin{align*} &(-2\text{i})^3+\left(-2\sqrt{3}+2\text{i}\right)\times (-2\text{i})^2+\left(4-4\text{i}\sqrt{3}\right)\times (-2\text{i})+8\text{i}\\
- Vérifier que, pour tout nombre complexe $z$, on a : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = (z + 2i)\left(z^2 - 2\sqrt{3} z + 4\right).\] On a :
- Résoudre l'équation $(E)$ dans l'ensemble des nombres complexes. Un produit de facteurs est nul si, et seulement si, un de ses facteurs au moins est nul.
- Écrire les solutions de l'équation $(E)$ sous forme exponentielle. $-2\text{i}=2\text{e}^{-\text{i}\pi/2}$
=& 8\text{i} -4\left(-2\sqrt{3}+2\text{i}\right)-\left(8\text{i}+8\sqrt{3}\right)+8\text{i}\\
=& 8\text{i}+8\sqrt{3}-8\text{i}-8\text{i}-8\sqrt{3}+8\text{i}\\
=& 0\end{align*}$
$-2\text{i}$ est donc une solution de l’équation $(E)$.
$\quad$
$\begin{align*}& (z+2\text{i})\left(z^2-2\sqrt{3}z+4\right)\\
=& z^3-2\sqrt{3}z^2+4z+2\text{i} z^2-4\text{i}\sqrt{3}z+8\text{i} \\
=& z^3+\left(2\text{i}-2\sqrt{3}\right)z^2+\left(4-4\text{i}\sqrt{3}\right)z+8\text{i}\end{align*}$
$\quad$
Donc $(E)\iff z+2\text{i}=0$ ou $z^2-2\sqrt{3}z+4=0$
$z+2\text{i} =0\iff z=-2\text{i}$
On considère maintenant l’équation $z^2-2\sqrt{3}z+4=0$
$\Delta=\left(-2\sqrt{3}\right)^2-4\times 1\times 4=-4<0$
Les solutions de cette équation sont donc :
$z_1=\dfrac{2\sqrt{3}-2\text{i}}{2}=\sqrt{3}-\text{i}$ et $z_2=\overline{z_1}=\sqrt{3}+\text{i}$
Ainsi les solutions de l’équation $(E)$ sont $-2\text{i}$, $\sqrt{3}+\text{i}$ et $\sqrt{3}-\text{i}$.
$\quad$
$\left|\sqrt{3}+\text{i}\right|=2$ donc $\sqrt{3}+\text{i}=2\left(\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right)=2\text{e}^{\text{i}\pi/6}$
et $\sqrt{3}-\text{i}=2\text{e}^{-\text{i}\pi/6}$
$\quad$
Dans la suite, on se place dans le plan muni d'un repère orthonormé direct d'origine $O$.
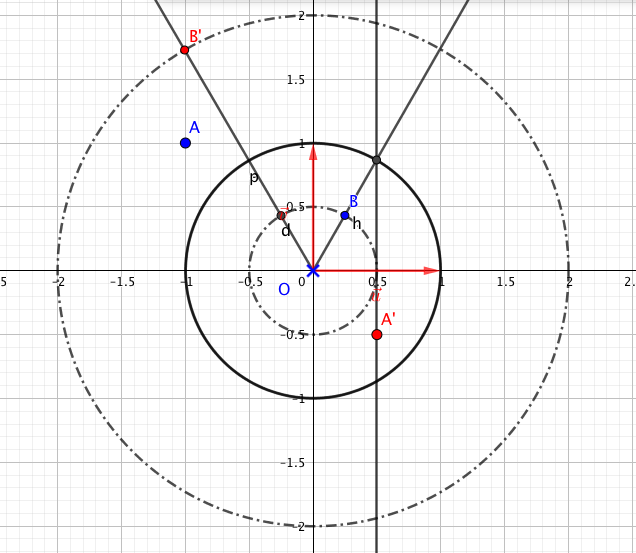
- On considère les points A, B, C d'affixes respectives $-2i$, $\sqrt{3} + \text{i}$ et $\sqrt{3} - \text{i}$.
- Montrer que A, B et C appartiennent à un même cercle de centre O dont on déterminera le rayon. Les trois nombres complexes sont tous de module $2$.
- Placer ces points sur une figure que l'on complètera par la suite. Voir figure en fin d’exercice
- On note D le milieu du segment [OB]. Déterminer l'affixe $z_{\text{L}}$ du point L tel que AODL soit un parallélogramme. $D$ est le milieu du segment $[OB]$.
Par conséquent $OA=OB=OC=2$.
Les points $A$, $B$ et $C$ appartiennent donc au cercle de centre $O$ et de rayon $2$.
$\quad$
$\quad$
Ainsi $z_D=\dfrac{z_O+z_B}{2}=\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}$.
$\quad$
$AODL$ est un parallélogramme
$\iff \vec{AL}=\vec{OD}$
$\iff z_L-z_A=z_D-z_O$
$\iff z_L=z_D+z_A$
$\iff z_L=\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}-2\text{i}$
$\iff z_L=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}$
$\quad$ - On rappelle que, dans un repère orthonormé du plan, deux vecteurs de coordonnées respectives $(x~;~y)$ et $(x'~;~y')$ sont orthogonaux si et seulement si $xx'+yy' = 0$.
- Soit $\vec{u}$ et $\vec{v}$ deux vecteurs du plan, d'affixes respectives $z$ et $z'$. Montrer que $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si $z \overline{z'}$ est un imaginaire pur. On note $z=x+\text{i} y$ et $z’=x’+\text{i} y’$.
- À l'aide de la question 3. a. , démontrer que le triangle AOL est rectangle en L. L’affixe du vecteur $\vec{OL}$ est $z=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}$
Ainsi
$\begin{align*} z\overline{z’}&=(x+\text{i} y)\left(x’-\text{i} y’\right)\\
&=xx’-\text{i} xy’+\text{i} yx’+yy’ \\
&=xx’+yy’+(x’y-xy’)\text{i}\end{align*}$
Par conséquent :
$z\overline{z’}$ est un imaginaire pur
$\iff xx’+yy’=0$
$\iff \vec{u}$ et $\vec{v}$ sont orthogonaux
$\quad$
L’affixe du vecteur $\vec{AL}$ est $z’=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}+2\text{i}=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}+\dfrac{\text{i}}{2}$.
Ainsi :
$\begin{align*} z\overline{z’}&=\left(\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}\right)\left(\dfrac{\sqrt{3}}{2}-\dfrac{\text{i}}{2}\right) \\
&=\dfrac{3}{4}-\dfrac{\sqrt{3}\text{i}}{4}-\dfrac{3\text{i}\sqrt{3}}{4}-\dfrac{3}{4} \\
&=-\text{i}\sqrt{3}\end{align*}$
$z\overline{z’}$ est donc un imaginaire pur. Les vecteurs $\vec{OL}$ et $\vec{AL}$ sont donc orthogonaux et le triangle $AOL$ est rectangle en $L$.
$\quad$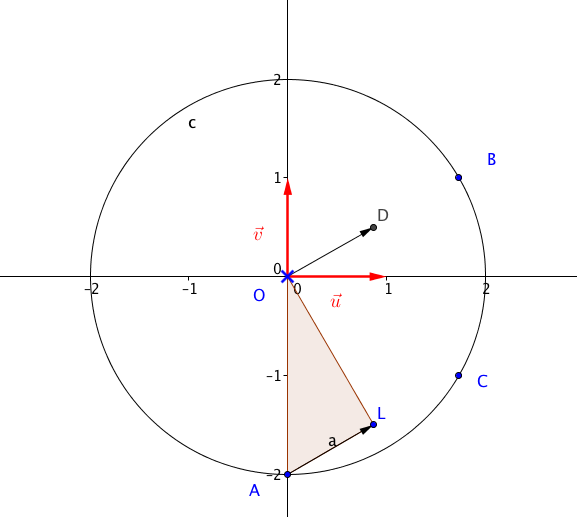
Spécialité 5 points
On note $r$ l'ensemble des matrices colonnes à 2 lignes, à coefficients entiers. Soit $U = \begin{pmatrix}u_1\\u_2\end{pmatrix}$ et $V = \begin{pmatrix}v_1\\v_2\end{pmatrix}$ deux éléments de $r$.
À $U$ et $V$, on associe la matrice $A = \begin{pmatrix}u_1&v_1\\u_2&v_2\end{pmatrix}$ et le nombre $d(A) = u_1 v_2 - u_2v_1$.
On dit que $(U,~V)$ est une base de $r$ si et seulement si, pour tout élément $X$ de $r$, il existe un unique couple d'entiers relatifs $(a~;~b)$ tel que $X = aU + bV$.
- Dans cette question, on pose $U = \begin{pmatrix}2\\1\end{pmatrix}$, \:$V = \begin{pmatrix}1\\2\end{pmatrix}$ et $X = \begin{pmatrix}10\\10\end{pmatrix}$
- Montrer que $X$ ne peut pas s'écrire $X = a U + b V$, avec $a$ et $b$ entiers relatifs.
- Le couple $(U,~ V)$ est-il une base de $r$ ?
Dans la suite de l'exercice, on souhaite illustrer sur un exemple la propriété : « si $d(A) = 1$, alors $(U, V)$ est une base de $r$ » .
- En posant $U = \begin{pmatrix}6\\- 11\end{pmatrix}$ le but de cette question est de déterminer $V \begin{pmatrix}v_1\\v_2\end{pmatrix}$ tel que $d(A) = 1$. On rappelle dans ce cas que la matrice $A$ associée au couple $(U,~ V)$ s'écrit : $A = \begin{pmatrix}6&v_1\\- 11&v_2\end{pmatrix}$.
- Exprimer la condition $d(A) = 1$ par une égalité reliant $v_1$ et $v_2$.
- On considère l'équation $(E) :\: 11 x + 6 y = l$, où $x$ et $y$ sont des entiers relatifs. Donner une solution particulière de l'équation $(E)$.
- Résoudre l'équation $(E)$ dans l'ensemble des entiers relatifs.
- Déterminer alors une matrice $V \begin{pmatrix}v_1\\v_2\end{pmatrix}$ de $r$ vérifiant d'une part l'égalité $d(A) = 1$ et, d' autre part, la condition $0 \leqslant v_1 \leqslant 10$.
- Dans cette question, on pose $U = \begin{pmatrix}6\\- 11\end{pmatrix}$ et $V = \begin{pmatrix}5\\- 9\end{pmatrix}$. Ainsi $A = \begin{pmatrix}6&5\\- 11&-9\end{pmatrix}$.
- Montrer que la matrice $A$ est inversible et donner sa matrice inverse $A^{-1}$.
- Soit $X$ un élément de $r$. Montrer que l'égalité $X = aU + b V$ s'écrit matriciellement $X = A\begin{pmatrix}a\\b\end{pmatrix}$.
- Déduire des questions précédentes qu'il existe un unique couple d'entiers relatifs $(a~;~b)$ tel que $X = aU +bV$, c'est-à-dire tel que $(U,~ V)$ est une base de $r$.
- Déterminer ce couple $(a~;~b)$ lorsque $X = \begin{pmatrix}2\\3\end{pmatrix}$.
Correction de l'exercice de Spécialité 5 points
On note $r$ l'ensemble des matrices colonnes à 2 lignes, à coefficients entiers. Soit $U = \begin{pmatrix}u_1\\u_2\end{pmatrix}$ et $V = \begin{pmatrix}v_1\\v_2\end{pmatrix}$ deux éléments de $r$.
À $U$ et $V$, on associe la matrice $A = \begin{pmatrix}u_1&v_1\\u_2&v_2\end{pmatrix}$ et le nombre $d(A) = u_1 v_2 - u_2v_1$.
On dit que $(U,~V)$ est une base de $r$ si et seulement si, pour tout élément $X$ de $r$, il existe un unique couple d'entiers relatifs $(a~;~b)$ tel que $X = aU + bV$.
- Dans cette question, on pose $U = \begin{pmatrix}2\\1\end{pmatrix}$, \:$V = \begin{pmatrix}1\\2\end{pmatrix}$ et $X = \begin{pmatrix}10\\10\end{pmatrix}$
- Montrer que $X$ ne peut pas s'écrire $X = a U + b V$, avec $a$ et $b$ entiers relatifs. On considère deux entiers relatifs $a$ et $b$.
- Le couple $(U,~ V)$ est-il une base de $r$ ? $X=\begin{pmatrix}10\\10\end{pmatrix}$ ne peut pas s’écrire sous la forme $aU+bV$.
$aU+BV=\begin{pmatrix}2a+b\\a+2b\end{pmatrix}$
Ainsi :
$\begin{align*} X=aU+bV&\iff \begin{cases} 2a+b=10\\a+2b=10\end{cases} \\
&\iff \begin{cases} b=10-2a\\a+2(10-2a)=10\end{cases} \\
&\iff \begin{cases} b=10-2a\\-3a+20=10\end{cases} \\
&\iff \begin{cases} b=10-2a\\-3a=-10\end{cases}\end{align*}$
$10$ n’est pas divisible par $3$ donc l’équation $-3a=-10$ ne possède pas de solution dans $\mathbb Z$.
$X$ ne peut donc pas s’écrire sous la forme $X=aU+bV$ avec $a$ et $b$ entiers relatifs.
$\quad$
Par conséquent $(U,V)$ n’est pas une base de $r$.
$\quad$
Dans la suite de l'exercice, on souhaite illustrer sur un exemple la propriété : « si $d(A) = 1$, alors $(U, V)$ est une base de $r$ » .
- En posant $U = \begin{pmatrix}6\\- 11\end{pmatrix}$ le but de cette question est de déterminer $V \begin{pmatrix}v_1\\v_2\end{pmatrix}$ tel que $d(A) = 1$. On rappelle dans ce cas que la matrice $A$ associée au couple $(U,~ V)$ s'écrit : $A = \begin{pmatrix}6&v_1\\- 11&v_2\end{pmatrix}$.
- Exprimer la condition $d(A) = 1$ par une égalité reliant $v_1$ et $v_2$. $d(A)=1\iff 6v_2+11v_1=1$
- On considère l'équation $(E) :\: 11 x + 6 y = l$, où $x$ et $y$ sont des entiers relatifs. Donner une solution particulière de l'équation $(E)$. $11\times (-1)+6\times 2=-11+12=1$
- Résoudre l'équation $(E)$ dans l'ensemble des entiers relatifs. On considère une solution $(x;y)$ de l’équation $(E)$.
- Déterminer alors une matrice $V \begin{pmatrix}v_1\\v_2\end{pmatrix}$ de $r$ vérifiant d'une part l'égalité $d(A) = 1$ et, d' autre part, la condition $0 \leqslant v_1 \leqslant 10$. D’après la question précédente, il existe un entier relatif $k$ tel que $v_1=6k-1$ et $v_2=2-11k$.
$\quad$
Le couple $(-1;2)$ est donc une solution particulière de l’équation $(E)$.
$\quad$
On a donc $11\times (-1)+6\times 2=1$ et $11x+6y=1$.
Par différence, on obtient $11(-1-x)+6(2-y)=0 \iff 6(2-y)=11(1+x)$.
$6$ et $11$ sont premiers entre eux.
D’après le théorème de Gauss, il existe un entier relatif $k$ tel que $2-y=11k$ et $1+x=6k$.
Par conséquent $x=6k-1$ et $y=2-11k$.
$\quad$
Réciproquement, on considère un entier relatif $k$.
$11(6k-1)+6(2-11k)=66k-11+12-66k=1$
$\quad$
Les solutions de l’équation $(E)$ sont donc les couples $(6k-1;2-11k)$ pour $k\in\mathbb Z$.
$\quad$
De plus :
$0\leq v_1\leq 10\iff 0\leq 6k-1\leq 10 \iff 1\leq 6k \leq 9 \iff \dfrac{1}{6} \leq k\leq \dfrac{3}{2} \iff k=1$.
Ainsi $v_1=5$ et $v_2=-9$
Par conséquent $V=\begin{pmatrix} 5\\-9\end{pmatrix}$.
$\quad$ - Dans cette question, on pose $U = \begin{pmatrix}6\\- 11\end{pmatrix}$ et $V = \begin{pmatrix}5\\- 9\end{pmatrix}$. Ainsi $A = \begin{pmatrix}6&5\\- 11&-9\end{pmatrix}$.
- Montrer que la matrice $A$ est inversible et donner sa matrice inverse $A^{-1}$. On considère les matrices $A=\begin{pmatrix}6&5\\-11&-9\end{pmatrix}$ et $B=\begin{pmatrix}-9&-5\\11&6\end{pmatrix}$
- Soit $X$ un élément de $r$. Montrer que l'égalité $X = aU + b V$ s'écrit matriciellement $X = A\begin{pmatrix}a\\b\end{pmatrix}$. Soit $X=\begin{pmatrix}x\\y\end{pmatrix}$ un élément de $r$.
- Déduire des questions précédentes qu'il existe un unique couple d'entiers relatifs $(a~;~b)$ tel que $X = aU +bV$, c'est-à-dire tel que $(U,~ V)$ est une base de $r$. $X=A\begin{pmatrix}a\\b\end{pmatrix}\iff \begin{pmatrix}a\\b\end{pmatrix}=A^{-1}X$.
- Déterminer ce couple $(a~;~b)$ lorsque $X = \begin{pmatrix}2\\3\end{pmatrix}$. Si $X=\begin{pmatrix}2\\3\end{pmatrix}$ alors :
$\begin{align*}AB&=\begin{pmatrix}-9\times 6+5\times 11&6\times (-5)+5\times 6\\-11\times (-9)+-9\times 11&-11\times (-5)+6\times (-9)\end{pmatrix} \\
&=\begin{pmatrix}1&0\\0&1\end{pmatrix}\end{align*}$
On obtient de même $BA=\begin{pmatrix}1&0\\0&1\end{pmatrix}$.
La matrice $A$ est donc inversible et $A^{-1}=\begin{pmatrix}-9&-5\\11&6\end{pmatrix}$.
$\quad$
$\begin{align*} X=aU+bV&\iff \begin{pmatrix}x\\y\end{pmatrix}=a\begin{pmatrix}6\\-11\end{pmatrix}+b\begin{pmatrix}5\\-9\end{pmatrix} \\
&\iff \begin{cases}x=6a+5b\\y=-11a-9b\end{cases} \\
&\iff X=A\begin{pmatrix}a\\b\end{pmatrix}\end{align*}$
$\quad$
Ainsi pour une matrice $X$ de $r$ donnée il existe une unique matrice $\begin{pmatrix}a\\b\end{pmatrix}$ telle que $X=A\begin{pmatrix}a\\b\end{pmatrix}$.
$\quad$
$X=A\begin{pmatrix}a\\b\end{pmatrix}\iff \begin{pmatrix}a\\b\end{pmatrix}=A^{-1}\begin{pmatrix}2\\3\end{pmatrix}\iff \begin{pmatrix}a\\b\end{pmatrix}=\begin{pmatrix}-33\\40\end{pmatrix}$
$\quad$
- Vues: 105106