Baccalauréat S Antilles-Guyane 18 juin 2013 - Correction de l'Exercice 1

Page 2 sur 11: Correction de l'Exercice 1

Correction de l'Exercice 1 5 points

Commun à tous les candidats

Description de la figure dans l'espace muni du repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$: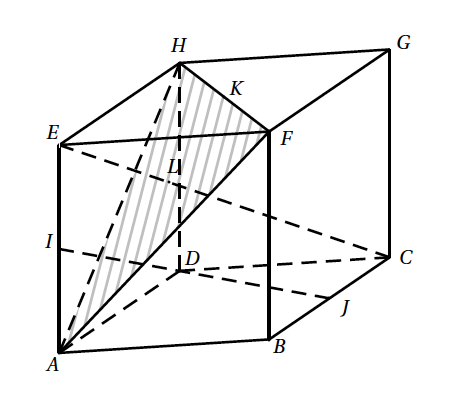

• $ABCDEFGH$ désigne un cube de côté 1.
• On appelle $\mathcal{P}$ le plan $(AFH)$.
• Le point $I$ est le milieu du segment $[AE]$,
• le point $J$ est le milieu du segment $[BC]$,
• le point $K$ est le milieu du segment $[HF]$,
• le point $L$ est le point d'intersection de la droite $(EC)$ et du plan $\mathcal{P}$.

Ceci est un questionnaire à choix multiples (QCM). Pour chacune des questions, une seule des quatre affirmations est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse choisie. Aucune justification n'est demandée.
Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte aucun point.

1. 1. Les droites $(IJ)$ et $(EC)$ sont strictement parallèles.
   2. Les droites $(IJ)$ et $(EC)$ sont non coplanaires.
   3. Les droites $(IJ)$ et $(EC)$ sont sécantes.
   4. Les droites $(IJ)$ et $(EC)$ sont confondues.
Les plans $(AEC)$ et $(IEC)$ sont confondus. J n’appartient pas à $(AEC)$. Réponse b

2. 1. Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 0.
   2. Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à $(-1)$.
   3. Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 1.
   4. Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 2.
$\vec{AF}.\vec{BG} = \left(\vec{AB}+\vec{BF} \right).\left(\vec{BC}+\vec{CG}\right)$ $=\left(\vec{AB}+\vec{AE} \right).\left(\vec{AD}+\vec{AE}\right)$
$\vec{AF}.\vec{BG} = \vec{AB}.\vec{AD} + \vec{AB}.\vec{AE} + \vec{AE}.\vec{AD} + \vec{AE}.\vec{AE}$ $=AE^2=1$. Réponse c

3. Dans le repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$:
   1. Le plan $\mathcal{P}$ a pour équation cartésienne : $x + y + z - 1=0$.
   2. Le plan $\mathcal{P}$ a pour équation cartésienne : $x- y + z=0$.
   3. Le plan $\mathcal{P}$ a pour équation cartésienne : $- x + y + z=0$.
   4. Le plan $\mathcal{P}$ a pour équation cartésienne : $x + y - z = 0$.
$\vec{AF}(1;0;1)$ et $\vec{AH}(0;1;1)$ sont $2$ vecteurs non colinéaires. Ce sont donc des vecteurs de base du plan $\mathcal{P}$. Il faut donc que le produit scalaire du vecteur normal au plan avec ces $2$ vecteurs soit nul.
$A(0;0;0) \in \mathcal{P}$ : ce ne peut donc pas être l’équation a.
Dans l’équation b : le vecteur normal est $\vec{n}(1;-1;1)$. Mais $\vec{n}.\vec{AF} = 1 + 1 =2$
Dans l’équation c : le vecteur normal est $\vec{n}(-1;1;1)$. Mais $\vec{n}.\vec{AH} = 1 + 1 =2$
Dans l’équation d : le vecteur normal est $\vec{n}(1;1;-1)$. Et $\vec{n}.\vec{AF} = 1 – 1 = 0$ et $\vec{n}.\vec{AH} = 1 – 1 = 0$. Réponse d

4. 1. $\vec{EG}$ est un vecteur normal au plan $\mathcal{P}$.
   2. $\vec{EL}$ est un vecteur normal au plan $\mathcal{P}$.
   3. $\vec{IJ}$ est un vecteur normal au plan $\mathcal{P}$.
   4. $\vec{DI}$ est un vecteur normal au plan $\mathcal{P}$.
Un vecteur normal est $\vec{n}(1;1;-1)$. Il faut donc que le vecteur choisi soit colinéaire à $\vec{n}$.
Or $\vec{EC}(1;1;-1)$. $\vec{EL}$ et $\vec{EC}$ sont colinéaires. Réponse b
$~$
5. 1. $\vec{AL}=\frac12\vec{AH} + \frac12\vec{AF}$.
   2. $\vec{AL}=\frac13\vec{AK}$.
   3. $\vec{ID}=\frac12\vec{IJ}$.
   4. $\vec{AL}=\frac13\vec{AB}+\frac13\vec{AD}+\frac23\vec{AE}$.

Déterminons les coordonnées de $L$.
Une équation paramétrique de $(EC)$ est :
$\left\{ \begin{array}{l} x=t \\\\ y=t \qquad t \in \mathbb R \\\\z = 1 -t \end{array} \right.$
Injectons ces équations dans l’équation de $\mathcal{P}$ : $t+t-1+t=0 \Leftrightarrow t = \dfrac{1}{3}$. Réponse d
$~$