Baccalauréat S Amérique du Nord 29 mai 2018 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

On se place dans l'espace muni d'un repère orthonormé dont l'origine est le point A. On considère les points B$(10~;~-8~;~2)$, C$(-1~;~-8~;~5)$ et D$(14~;~4~;~8)$.

1. 1. Déterminer un système d'équations paramétriques de chacune des droites (AB) et (CD).
   Un vecteur directeur de $(AB)$ est $\vec{AB}(10;-8;2)$.
   Un vecteur directeur de $(CD)$ est $\vec{CD}(15;12;3)$.
   Une représentation paramétrique de $(AB)$ est :
   $\begin{cases} x=10t\\y=-8t\\z=2t\end{cases} \quad, t\in \mathbb{R}$.
   Une représentation paramétrique de $(CD)$ est :
   $\begin{cases} x=-1+15k\\y=-8+12k\\z=5+3k\end{cases} \quad,k\in\mathbb{R}$
   Remarque : Attention à bien prendre deux paramètres différents pour la suite.
   $\quad$
   
   2. Vérifier que les droites (AB) et (CD) ne sont pas coplanaires.
   On a $\dfrac{10}{15}=\dfrac{2}{3}$
   Et $\dfrac{-8}{12}=-\dfrac{2}{3}$.
   Les coordonnées ne sont pas proportionnelles.
   Les vecteurs $\vec{AB}$ et $\vec{CD}$ ne sont pas colinéaires et les droites $(AB)$ et $(CD)$ ne sont pas parallèles.
   Regardons maintenant si les droites sont sécantes.
   Cherchons les solutions du système :
   $\begin{align*} \begin{cases} x=10t\\y=-8t\\z=2t\\x=-1+15k\\y=-8+12k\\z=5+3k\end{cases} &\iff \begin{cases} x=10t\\y=-8t\\z=2t\\10t=-1+15k\\-8t=-8+12k\\2t=5+3k \end{cases} \\
   &\iff \begin{cases} x=10t\\y=-8t\\z=2t\\10t=-1+15k \quad (1)\\-8t=-8+12k\\10t=25+15k \quad (2) \end{cases}
   \end{align*}$
   Les lignes $(1)$ et $(2)$ sont incompatibles. Il n’y a donc pas de point d’intersection.
   Les droites $(AB)$ et $(CD)$ ne sont pas coplanaires.
   $\quad$
2. On considère le point I de la droite (AB) d'abscisse 5 et le point J de la droite (CD) d'abscisse 4.
   1. Déterminer les coordonnées des points I et J et en déduire la distance IJ.
   L’abscisse du point $I$ est $5$.
   Par conséquent $10t=5 \iff t=0,5$.
   Ainsi les coordonnées du point $I$ sont $\begin{cases} x_I=5\\y_I=-4\\z_I=1\end{cases}$.
   $\quad$
   L’abscisse du point $J$ est $4$.
   par conséquent $-1+15k=4 \iff 15k=5 \iff k=\dfrac{1}{3}$.
   Ainsi les coordonnées du point $J$ sont $\begin{cases}x_J=4\\y_J=-4\\z_J=6\end{cases}$.
   $\quad$
   Donc :
   $\begin{align*} IJ&=\sqrt{(4-5)^2+\left(-4-(-4)\right)^2+(6-1)^2} \\
   &=\sqrt{1+0+25} \\
   &=\sqrt{26}
   \end{align*}$
   $\quad$
   2. Démontrer que la droite (IJ) est perpendiculaire aux droites (AB) et (CD). La droite (IJ) est appelée perpendiculaire commune aux droites (AB) et (CD).
   On a $\vec{IJ}(-1;0;5)$, $\vec{AB}(10;-8;2)$ et $\vec{CD}(15;12;3)$
   D’une part $\vec{IJ}.\vec{AB}=-10+0+10=0$
   D’autre part $\vec{IJ}.\vec{AB}=-15+0+15=0$.
   Le vecteur $\vec{IJ}$ est donc normal aux vecteurs $\vec{AB}$ et $\vec{CD}$.
   Les droites $(IJ)$ et $(AB)$ d’une part et $(IJ)$ et $(CD)$ d’autre part sont donc orthogonales.
   Mais $(IJ)$ et $(AB)$ sont sécantes en $I$ et les droites $(IJ)$ et $(CD)$ sont sécantes en $J$.
   La droite $(IJ)$ est donc perpendiculaire aux droites $(AB)$ et $(CD)$.
   $\quad$
3. Cette question a pour but de vérifier que la distance IJ est la distance minimale entre les droites (AB) et (CD). Sur le schéma ci -dessous on a représenté les droites (AB) et (CD), les points I et J, et la droite $\Delta$ parallèle à la droite (CD) passant par I. On considère un point $M$ de la droite (AB) distinct du point I. On considère un point $M'$ de la droite (CD) distinct du point J.
   
   
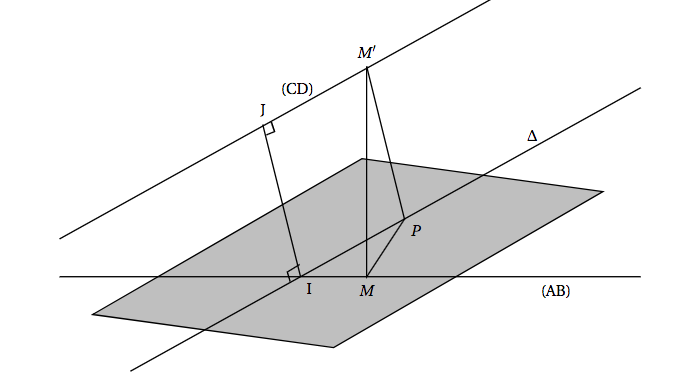
   1. Justifier que la parallèle à la droite (IJ) passant par le point $M'$ coupe la droite $\Delta$ en un point que l'on notera $P$.
   Le point $I$ n’appartenant pas à la droite $(CD)$; le point $I$ et la droite $(CD)$ définissent le plan $(IJM’)$.
   La droite $\Delta$ est parallèle à $(CD)$ et passe par le point $I$ : elle est donc incluse dans le plan $(IJM’)$.
   Ainsi, dans le plan $(IJM’)$, les droites $(JM’)$ et $\Delta$ sont parallèles et la droite $(IJ)$ est perpendiculaire à la droite $\Delta$.
   La droite parallèle à la droite $(IJ)$ passant par le point $M’$ est donc également perpendiculaire à la droite $\Delta$ : ces deux droites ont bien un point d’intersection appelé $P$.
   $\quad$
   
   2. Démontrer que le triangle $MPM'$ est rectangle en $P$.
   Les droites $(IJ)$ et $(M’P)$ sont parallèles par conséquent les vecteurs $\vec{IJ}$ et $\vec{M’P}$ sont colinéaires.
   Le vecteur $\vec{M’P}$ est alors orthogonal à $\vec{IP}$ ($(M’P)$ et $\Delta$ sont perpendiculaires) et à $\vec{IM}$ (car $\vec{IJ}$ et $\vec{AB}$ le sont).
   La droite $\Delta$ est parallèle à $(CD)$. D’après la question 1.b. elle n’est donc pas parallèle à la droite $(AB)$.
   Les droites $\Delta$ et $(AB)$ sont sécantes en $I$ : elles définissent le plan $(IMP)$.
   Le vecteur $\vec{M’P}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(IMP)$. Il est par conséquent orthogonal à tous les vecteurs de ce plan en particulier à $\vec{MP}$.
   Le triangle $MPM’$ est ainsi rectangle en $P$.
   $\quad$
   
   3. Justifier que $MM' > IJ$ et conclure.
   Dans un triangle rectangle, la longueur de l’hypoténuse est plus grande que la longueur des deux côtés de l’angle droit.
   Ainsi $MM’> M’P$ or $IJ=M’P$.
   Par conséquent $MM’>IJ$.