Baccalauréat S Amérique du Nord 29 mai 2018 - Correction Exercice 2
Page 4 sur 10
Correction de l'exercice 2 (4 points)
Lors d'une expérience en laboratoire, on lance un projectile dans un milieu fluide. L'objectif est de déterminer pour quel angle de tir $\theta$ par rapport à l'horizontale la hauteur du projectile ne dépasse pas $1,6$ mètre. Comme le projectile ne se déplace pas dans l'air mais dans un fluide, le modèle parabolique usuel n'est pas adopté. On modélise ici le projectile par un point qui se déplace, dans un plan vertical, sur la courbe représentative de la fonction $f$ définie sur l'intervalle [0 ; 1[ par: \[f(x) = bx + 2\ln (1- x)\] où $b$ est un paramètre réel supérieur ou égal à $2$, $x$ est l'abscisse du projectile, $f(x)$ son ordonnée, toutes les deux exprimées en mètres. 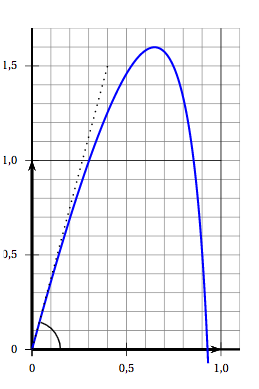
- La fonction $f$ est dérivable sur l'intervalle [0 ; 1[. On note $f'$ sa fonction dérivée. On admet que la fonction $f$ possède un maximum sur l'intervalle [0 ; 1[ et que, pour tout réel $x$ de l'intervalle [0 ; 1[ : \[f'(x) = \dfrac{- bx + b - 2}{1 - x}.\] Montrer que le maximum de la fonction $f$ est égal à $b - 2 + 2\ln \left(\dfrac{2}{b}\right)$. Etudions le signe de la dérivée :
- Déterminer pour quelles valeurs du paramètre $b$ la hauteur maximale du projectile ne dépasse pas $1,6$ mètre. On considère la fonction $g$ définie sur $[2;+\infty[$ par $g(x)=x-2+2\ln\left(\dfrac{2}{x}\right)$.
- Dans cette question, on choisit $b = 5,69$. L'angle de tir $\theta$ correspond à l'angle entre l'axe des abscisses et la tangente à la courbe de la fonction $f$ au point d'abscisse $0$ comme indiqué sur le schéma donné ci-dessus. Déterminer une valeur approchée au dixième de degré près de l'angle $\theta$. On a $f'(x)=\dfrac{-5,69x+5,69-2}{1-x}$
$f$ admet un maximum sur l’intervalle $[0;1[$ quand :
$\begin{align*} f'(x)=0 &\iff \dfrac{-bx+b-2}{1-x}=0 \\
&\iff -bx+b-2=0 \\
&\iff bx=b-2 \\
&\iff x=1-\dfrac{2}{b}
\end{align*}$
Le maximum est donc :
$\begin{align*} f\left(1-\dfrac{2}{b}\right)&=b-2+2\ln\left(1-1+\dfrac{2}{b}\right)\\
&=b-2+2\ln\left(\dfrac{2}{b}\right)\end{align*}$
$\quad$ Par ailleurs ici $x\in [0 ; 1[$, donc $x<1$, donc $ 1-x > 0$.
La fonction $g$ est dérivable sur $[2;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
$g'(x)=1+2\times \dfrac{-\dfrac{2}{x^2}}{\dfrac{2}{x}}=1-\dfrac{2}{x}=\dfrac{x-2}{x}$.
Etude du signe de la dérivée :
On travaille sur $[2;+\infty[$, donc $x-2\geq 0$ et $x>0$, donc $g'(x)\geq 0$.
$ g'(x)=0\iff x=2$.
La fonction $g$ est donc strictement croissante et continue (car dérivable) sur l’intervalle $[2;+\infty[$.
$g(2)=0<1,6$
$g(x)=x\left(1-\dfrac{2}{x}+\dfrac{2}{x}\ln\left(\dfrac{2}{x}\right)\right)$
$\lim\limits_{x \to +\infty} \dfrac{2}{x}= 0$ et $\lim\limits_{t \to 0} t\ln t=0$.
Donc par composée $\lim\limits_{x \to +\infty} g(x)=+\infty$.
Ainsi $1,6\in [0;+\infty[$.
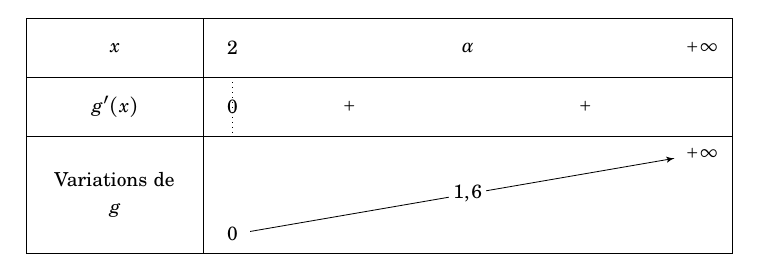
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $g(x)=1,6$ possède donc, sur l’intervalle $[2;+\infty[$ une unique solution $\alpha \approx 5,69$.
La fonction $g$ est strictement croissante.
Ainsi la hauteur maximale du projectile ne dépasse pas $1,6$ mètre quand $b$ appartient à l’intervalle $[2;\alpha]$.
$\quad$
Donc $f'(0)=3,69$.
Un vecteur directeur de la tangente est par conséquent $\vec{u}(1;3,69)$.
Par conséquent $\tan \theta =\dfrac{3,69}{1}$ donc $\theta \approx 74,8$°.
$\quad$
- Vues: 35123
