Baccalauréat S Amérique du Nord 29 mai 2018 - Exercice 3

Page 5 sur 10: Exercice 3

Exercice 3 5 points

Géométrie

On se place dans l'espace muni d'un repère orthonormé dont l'origine est le point A. On considère les points B$(10~;~-8~;~2)$, C$(-1~;~-8~;~5)$ et D$(14~;~4~;~8)$.

1. 1. Déterminer un système d'équations paramétriques de chacune des droites (AB) et (CD).
   2. Vérifier que les droites (AB) et (CD) ne sont pas coplanaires.
2. On considère le point I de la droite (AB) d'abscisse 5 et le point J de la droite (CD) d'abscisse 4.
   1. Déterminer les coordonnées des points I et J et en déduire la distance IJ.
   2. Démontrer que la droite (IJ) est perpendiculaire aux droites (AB) et (CD). La droite (IJ) est appelée perpendiculaire commune aux droites (AB) et (CD).
3. Cette question a pour but de vérifier que la distance IJ est la distance minimale entre les droites (AB) et (CD). Sur le schéma ci -dessous on a représenté les droites (AB) et (CD), les points I et J, et la droite $\Delta$ parallèle à la droite (CD) passant par I. On considère un point $M$ de la droite (AB) distinct du point I. On considère un point $M'$ de la droite (CD) distinct du point J.
   
   
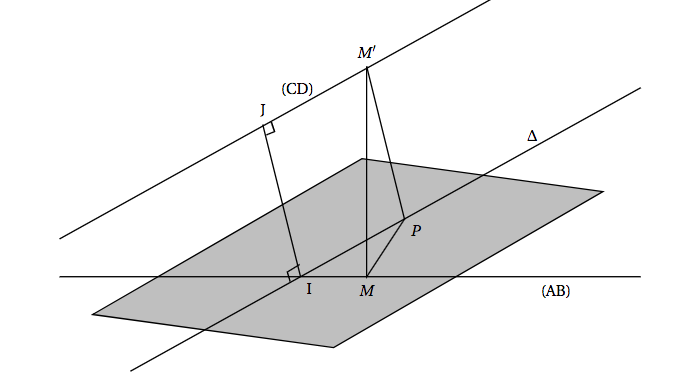
   1. Justifier que la parallèle à la droite (IJ) passant par le point $M'$ coupe la droite $\Delta$ en un point que l'on notera $P$.
   2. Démontrer que le triangle $MPM'$ est rectangle en $P$.
   3. Justifier que $MM' > IJ$ et conclure.