Baccalauréat S Centres étrangers 11 juin 2018 - Correction Exercice 4
Correction de l'exercice 4 5 points
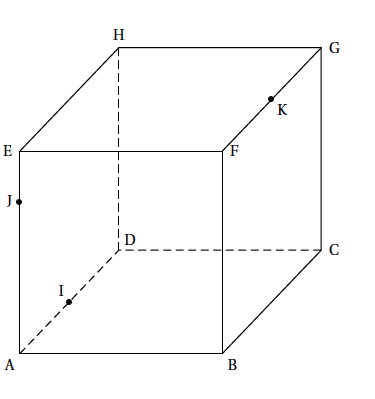
La figure ci-dessous représente un cube ABCDEFGH. Les trois points I, J, K sont définis par les conditions suivantes :
- I est le milieu du segment [AD] ;
- J est tel que $\vec {\text{AJ}} = \dfrac{3}{4} \vec {\text{AE}}$ ;
- K est le milieu du segment [FG].
Partie A
- Sur la figure donnée en annexe, construire sans justifier le point d'intersection P du plan (IJK) et de la droite (EH). On laissera les traits de construction sur la figure.
- En déduire, en justifiant, l'intersection du plan (IJK) et du plan (EFG). Les points $K$ et $P$ appartiennent aux plans $(IJK)$ et $(EFG)$.
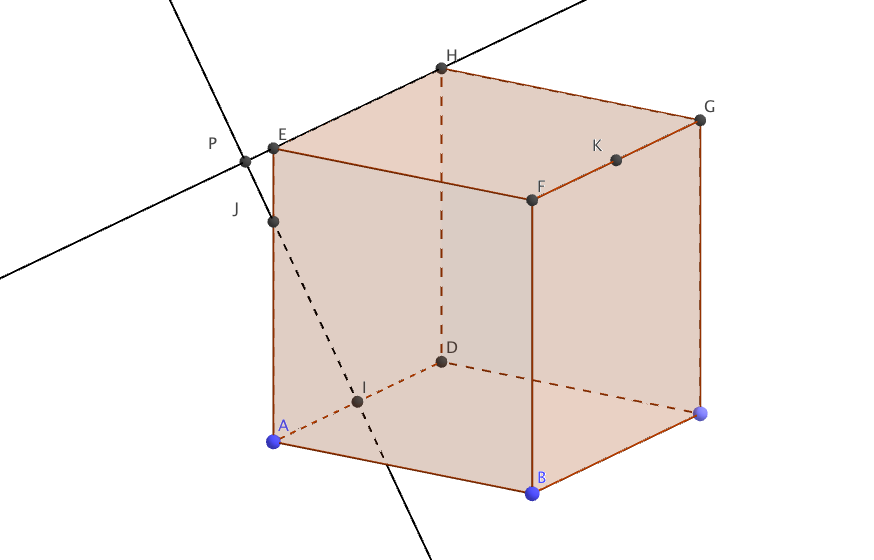 Le point $P$ est l’intersection de la droite $(IJ)$ avec la droite $(EH)$.
Le point $P$ est l’intersection de la droite $(IJ)$ avec la droite $(EH)$.$\quad$
La droite $(KP)$ est donc incluses dans les deux plans.
C’est par conséquent l’intersection de ces deux plans.
$\quad$
Partie B
On se place désormais dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$.
-
- Donner sans justification les coordonnées des points I, J et K. Le point $I$ est le milieu du segment $[AD]$.
- Déterminer les réels $a$ et $b$ tels que le vecteur $\vec {n} (4~;~a~;~b)$ soit orthogonal aux vecteurs $\vec {\text{IJ}}$ et $\vec {\text{IK}}$. On a $\vec{IJ}(0;-0,5;0,75)$ et $\vec{IK}(1;0;1)$.
- En déduire qu'une équation cartésienne du plan (IJK) est : $4x - 6y - 4z + 3 = 0$. Le vecteur $\vec{n}$ est orthogonal a deux vecteurs non colinéaires du plan $(IJK)$ (les coordonnées nulles ne sont pas les mêmes).
Par conséquent le point $I$ a pour coordonnées $(0;0,5;0)$.
On a $\vec{AJ}=\dfrac{3}{4}\vec{AE}$.
Le point $J$ a donc pour coordonnées $(0;0;0,75)$.
$K$ est le milieu du segment $[FG]$.
Par conséquent le point $K$ a pour coordonnées $(1;0,5;1)$
$\quad$
$\vec{n}$ orthogonal aux vecteurs $\vec{IJ}$ et $\vec{IK}$
$\iff \vec{n}.\vec{IJ}=0$ et $\vec{n}.\vec{IK}=0$
$\iff \begin{cases} -0,5a+0,75b=0 \\4+b=0 \end{cases}$
$\iff \begin{cases} b=-4\\-0,5a-0,75\times 4=0 \end{cases} $
$\iff \begin{cases} b=-4\\a=-6\end{cases}$
Ainsi le vecteur $\vec{n}$ a pour coordonnées $(4;-6;-4)$.
$\quad$
Ainsi une équation du plan $(IJK)$ est de la forme $4x-6y-4z+d=0$.
Le point $I(0;0,5;0)$ appartient à ce plan donc :
$0-3-0+d=0 \iff d=3$.
Une équation cartésienne du plan $(IJK)$ est donc $4x-6y-4z+3=0$.$\quad$ -
- Donner une représentation paramétrique de la droite (CG). Un vecteur directeur de la droite $(CG)$ est $\vec{CG}(0;0;1)$.
- Calculer les coordonnées du point N, intersection du plan (IJK) et de la droite (CG). Les coordonnées du point $N$ sont solutions du système suivant :
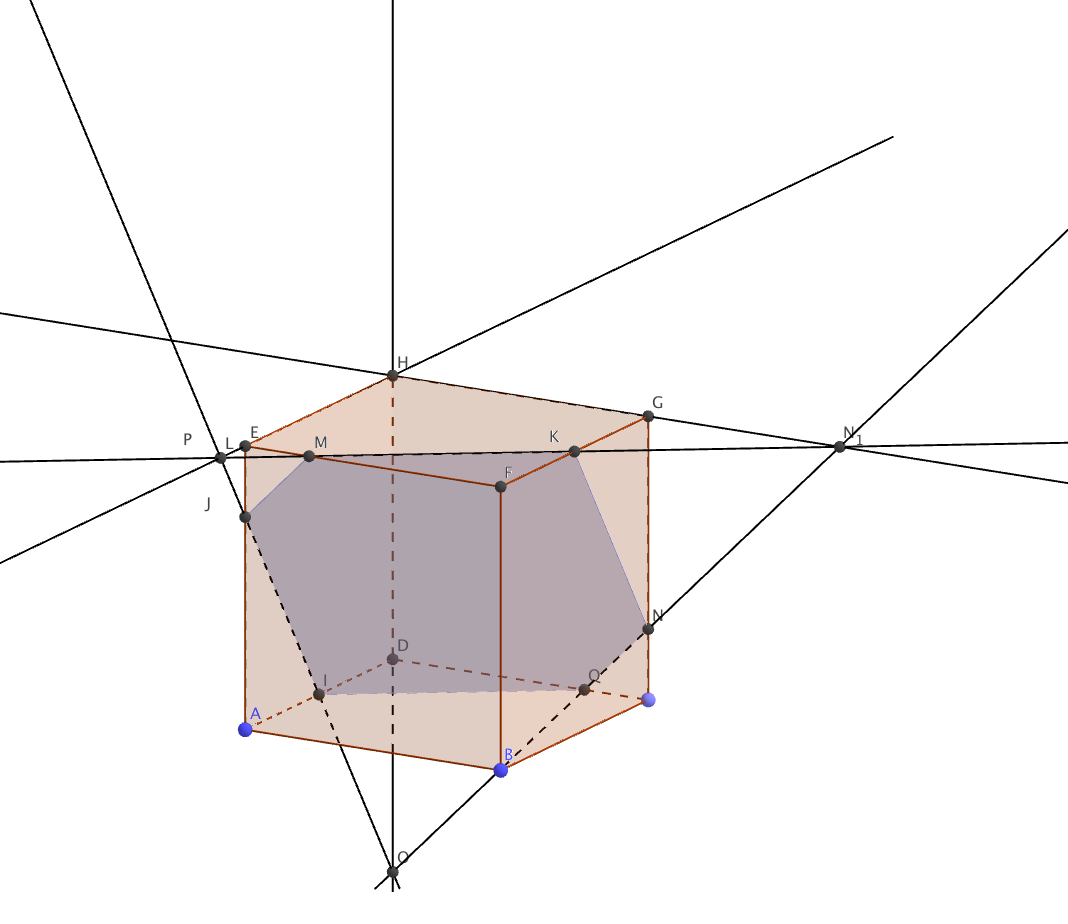
- Placer le point N sur la figure et construire en couleur la section du cube par le plan (IJK).
De plus le point $C$ a pour coordonnées $(1;1;0)$.
Une représentation paramétrique de la droite $(CG)$ est donc $\begin{cases} x=1 \\y=1\\z=t\end{cases} \quad, t \in \mathbb R$.
$\quad$
$\begin{align*} \begin{cases}x=1\\y=1\\z=t\\4x-6y-4z+3=0 \end{cases} &\iff \begin{cases} x=1\\y=1\\z=t\\4-6-4t+3=0\end{cases} \\
&\iff \begin{cases} x=1\\y=1\\z=t\\1-4t=0\end{cases} \\
&\iff \begin{cases} x=1\\y=1\\z=t\\t=0,25\end{cases}
\end{align*}$
Ainsi le point $N$ a pour coordonnées $(1;1;0,25)$.
$\quad$
Partie C
La droite $(FR)$ est orthogonale au plan $(IJK)$. Le vecteur $\vec{n}$ est donc un vecteur directeur de cette droite. Le point $F(1;0;1)$ appartient à cette droite.
Une représentation paramétrique de la droite $(FR)$ est ainsi $\begin{cases} x=1+4k\\y=-6k\\z=1-4k\end{cases}, k\in \mathbb R$.
Les coordonnées du point $R$ sont solutions du système suivant :
$\begin{align*} \begin{cases}x=1+4k\\y=-6k\\z=1-4k\\4x-6y-4z+3=0\end{cases}&\iff \begin{cases}x=1+4k\\y=-6k\\z=1-4k\\4+16k+36k-4+16k+3=0\end{cases} \\
&\iff \begin{cases}x=1+4k\\y=-6k\\z=1-4k\\68k+3=0\end{cases} \\
&\iff \begin{cases}x=1+4k\\y=-6k\\z=1-4k\\k=-\dfrac{3}{68}\end{cases} \\
&\iff \begin{cases}x=\dfrac{14}{17}\\y=\dfrac{9}{34}\\z=\dfrac{20}{17}\\k=-\dfrac{3}{68}\end{cases}
\end{align*}$
On a donc $z_R>1$.
Le point $R$ n’est pas à l’intérieur du cube.
$\quad$
- Vues: 40095
