Baccalauréat S Centres étrangers 11 juin 2018 - Correction Exercice 3
Correction de l'exercice 3 (7 points)
Les parties A et B sont indépendantes .
Un détaillant en fruits et légumes étudie l'évolution de ses ventes de melons afin de pouvoir anticiper ses commandes.
Partie A
Le détaillant constate que ses melons se vendent bien lorsque leur masse est comprise entre $900$ g et 1200 g. Dans la suite, de tels melons sont qualifiés « conformes ». Le détaillant achète ses melons auprès de trois maraîchers, notés respectivement A, B et C. Pour les melons du maraîcher A, on modélise la masse en gramme par une variable aléatoire $M_{\text{A}}$ qui suit une loi uniforme sur l'intervalle $[850~;~x]$, où $x$ est un nombre réel supérieur à 1200 . La masse en gramme des melons du maraîcher B est modélisée par une variable aléatoire $M_{\text{B}}$ qui suit une loi normale de moyenne 1050 et d'écart-type inconnu $\sigma$. Le maraîcher C affirme, quant à lui, que 80 % des melons de sa production sont conformes.
- Le détaillant constate que 75 % des melons du maraîcher A sont conformes. Déterminer $x$. $M_A$ suit une loi uniforme sur l’intervalle $[850;x]$.
- Il constate que 85 % des melons fournis par le maraîcher B sont conformes. Déterminer l'écart-type $\sigma$ de la variable aléatoire $M_{\text{B}}$. En donner la valeur arrondie à l'unité. La variable aléatoire $X=\dfrac{M_B-1~050}{\sigma}$ suit la loi normale centrée réduite.
- Le détaillant doute de l'affirmation du maraîcher C. Il constate que sur $400$ melons livrés par ce maraîcher au cours d'une semaine, seulement $294$ sont conformes. Le détaillant a-t-il raison de douter de l'affirmation du maraîcher C ? On a $n=400$ et $p=0,8$.
Ainsi $P\left(900\leqslant M_A\leqslant 1~200\right)=\dfrac{1~200-900}{x-850}=\dfrac{300}{x-850}$
Par conséquent
$\begin{align*} \dfrac{300}{x-850}&=0,75 &\iff 300=0,75x-637,5 \\
&\iff 937,5=0,75x \\
&\iff x = 1250
\end{align*}$
$\quad$
$\begin{align*} P\left(900\leqslant M_B\leqslant 1200\right)=0,85 &\iff P\left(-150\leqslant M_B-1~050 \leqslant 150\right)=0,85 \\
&\iff P\left(-\dfrac{150}{\sigma} \leqslant \dfrac{M_B-1~050}{\sigma} \leqslant \dfrac{150}{\sigma}\right) =0,85 \\
&\iff P\left(-\dfrac{150}{\sigma} \leqslant X \leqslant \dfrac{150}{\sigma}\right) =0,85 \\
&\iff 2P\left(X \leqslant \dfrac{150}{\sigma}\right)-1=0,85 \\
&\iff 2P\left(X \leqslant \dfrac{150}{\sigma}\right)=1,85 \\
&\iff P\left(X \leqslant \dfrac{150}{\sigma}\right)=0,925
\end{align*}$
À l’aide de la touche inverse loi normale de la calculatrice on trouve $\dfrac{150}{\sigma} \approx 1,440$.
Par conséquent $\sigma \approx 104$.
$\quad$
Donc $n\geqslant 30$, $np=320\geqslant 5$ et $n(1-p)=80\geqslant 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion de melons conformes est donc :
$\begin{align*} I_{400}&=\left[0,8-1,96\sqrt{\dfrac{0,8\times 0,2}{400}};0,8+1,96\sqrt{\dfrac{0,8\times 0,2}{400}}\right] \\
&=[0,760~8;0,839~2]
\end{align*}$
La fréquence observée est $f=\dfrac{294}{400}=0,735 \notin I_{400}$.
Au risque d’erreur de $5\%$, le détaillant a raison de douter de l’affirmation du maraîcher C.
$\quad$
Partie B
Le détaillant réalise une étude sur ses clients. Il constate que:
- parmi les clients qui achètent un melon une semaine donnée, 90 % d'entre eux achètent un melon la semaine suivante;
- parmi les clients qui n'achètent pas de melon une semaine donnée, 60 % d'entre eux n'achètent pas de melon la semaine suivante.
On choisit au hasard un client ayant acheté un melon au cours de la semaine 1 et, pour $n \geqslant 1$, on note $A_n$ l'évènement : « le client achète un melon au cours de la semaine $n$ ». On a ainsi $p\left(A_1\right) = 1$.
-
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
- Démontrer que $p\left(A_3\right) = 0,85$. D’après la formule des probabilités totales on a :
- Sachant que le client achète un melon au cours de la semaine 3, quelle est la probabilité qu'il en ait acheté un au cours de la semaine 2 ? Arrondir au centième. On veut calculer :
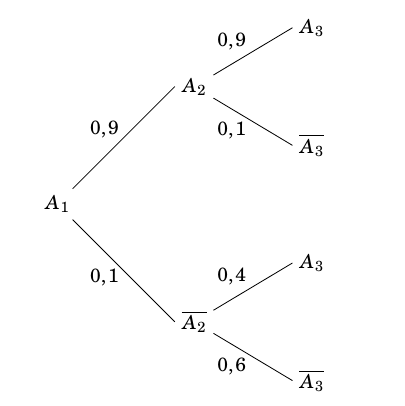
$\begin{align*} P\left(A_3\right)&=P\left(A_2\cap A_3\right)+P\left(\overline{A_2}\cap A_3\right) \\
&=0,9\times 0,9+0,1\times 0,4 \\
&=0,81+0,04 \\
&=0,85
\end{align*}$
$\quad$
$\begin{align*} P_{A_3}\left(A_2\right) &=\dfrac{P\left(A_2\cap A_3\right)}{P\left(A_3\right)} \\
&=\dfrac{0,9\times 0,9}{0,85} \\
&=\dfrac{81}{85} \\
&\approx 0,95
\end{align*}$
Dans la suite, on pose pour tout entier $n \geqslant 1$ : $p_n = P\left(A_n\right)$. On a ainsi $p_1 = 1$.
- Démontrer que, pour tout entier $n \geqslant 1$ : $p_{n+1} = 0,5p_n + 0,4$. On peut représenter la situation par l’arbre de probabilité suivant :
-
- Démontrer par récurrence que, pour tout entier $n \geqslant 1$ : $p_n > 0,8$. Initialisation : si $n=1$ alors $p_1=1 > 0,8$.
- Démontrer que la suite (p n) est décroissante. Soit $n$ un entier naturel non nul.
- La suite $\left(p_n\right)$ est-elle convergente ? La suite $\left(p_n\right)$ est décroissante et minorée par $0,8$. Elle est donc convergente.
La propriété est vraie au rang $1$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $p_n > 0,8$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $p_{n+1}> 0,8$.
$\begin{align*} p_n> 0,8&\iff 0,5p_n > 0,4 \\
&\iff 0,5p_n+0,4> 0,8 \\
&\iff p_{n+1} > 0,8
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul on a $p_n> 0,8$.
$\quad$
$\begin{align*} p_{n+1}-p_n&=0,5p_n+0,4-p_n \\
&=-0,5p_n+0,4 \\
&=0,5\left(-p_n+0,8\right)
\end{align*}$
On sait d’après la question précédente que $p_n> 0,8 \iff 0,8-p_n<0$.
Par conséquent $p_{n+1}-p_n<0$.
La suite $\left(p_n\right)$ est donc décroissante.
$\quad$
- On pose pour tout entier $n \geqslant 1$ : $v_n = p_n - 0,8$.
- Démontrer que $\left(v_n\right)$ est une suite géométrique dont on donnera le premier terme $v_1$ et la raison. Pour tout entier naturel $n \geqslant 1$ on a $v_n=p_n-0,8 \iff p_n=v_n+0,8$.
- Exprimer $v_n$ en fonction de $n$. En déduire que, pour tout $n \geqslant 1$, $p_n = 0,8 + 0,2 \times 0,5^{n-1}$. Par conséquent, pour tout entier $n\geqslant 1$ on a $v_n=0,2\times 0,5^{n-1}$.
- Déterminer la limite de la suite $\left(p_n\right)$. n a $-1<0,5<1$ donc $\lim\limits_{n\to +\infty} 0,5^n=0$. Par conséquent $\lim\limits_{n\to +\infty} 0,5^{n-1}=0$.
$\begin{align*} v_{n+1}&=p_{n+1}-0,8 \\
&=0,5p_n+0,4-0,8 \\
&=0,5p_n-0,4 \\
&=0,5\left(p_n+0,8\right)-0,4 \\
&=0,5p_n+0,4-0,4 \\
&=0,5p_n
\end{align*}$
La suite $\left(v_n\right)$ est donc géométrique de raison $0,5$ et de premier terme $v_1=p_1-0,8=0,2$.
$\quad$
Or $p_n=v_n+0,8=0,8+0,2\times 0,5^{n-1}$.
$\quad$
Et $\lim\limits_{n\to +\infty} p_n=0,8$.
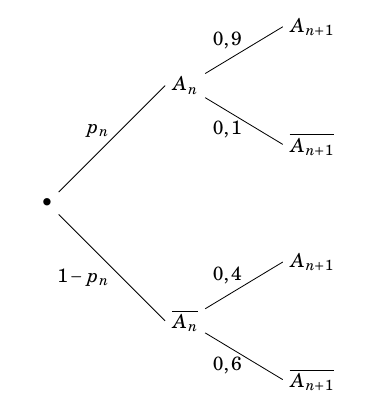
D’après la formule des probabilités totales, on a :
$\begin{align*} p_{n+1}&=P\left(A_n\cap A_{n+1}\right)+P\left(\overline{A_n}\cap A_{n+1}\right) \\
&=0,9p_n+0,4\left(1-p_n\right) \\
&=0,5p_n+0,4 \end{align*}$
$\quad$
- Vues: 40092
