Baccalauréat S Centres étrangers 11 juin 2018 - Exercice 3
Exercice 3 5 points
Les parties A et B sont indépendantes .
Un détaillant en fruits et légumes étudie l'évolution de ses ventes de melons afin de pouvoir anticiper ses commandes.
Partie A
Le détaillant constate que ses melons se vendent bien lorsque leur masse est comprise entre $900$ g et 1200 g. Dans la suite, de tels melons sont qualifiés « conformes ». Le détaillant achète ses melons auprès de trois maraîchers, notés respectivement A, B et C. Pour les melons du maraîcher A, on modélise la masse en gramme par une variable aléatoire $M_{\text{A}}$ qui suit une loi uniforme sur l'intervalle $[850~;~x]$, où $x$ est un nombre réel supérieur à 1200 . La masse en gramme des melons du maraîcher B est modélisée par une variable aléatoire $M_{\text{B}}$ qui suit une loi normale de moyenne 1050 et d'écart-type inconnu $\sigma$. Le maraîcher C affirme, quant à lui, que 80 % des melons de sa production sont conformes.
- Le détaillant constate que 75 % des melons du maraîcher A sont conformes. Déterminer $x$.
- Il constate que 85 % des melons fournis par le maraîcher B sont conformes. Déterminer l'écart-type $\sigma$ de la variable aléatoire $M_{\text{B}}$. En donner la valeur arrondie à l'unité.
- Le détaillant doute de l'affirmation du maraîcher C. Il constate que sur $400$ melons livrés par ce maraîcher au cours d'une semaine, seulement $294$ sont conformes. Le détaillant a-t-il raison de douter de l'affirmation du maraîcher C ?
Partie B
Le détaillant réalise une étude sur ses clients. Il constate que:
- parmi les clients qui achètent un melon une semaine donnée, 90 % d'entre eux achètent un melon la semaine suivante;
- parmi les clients qui n'achètent pas de melon une semaine donnée, 60 % d'entre eux n'achètent pas de melon la semaine suivante.
On choisit au hasard un client ayant acheté un melon au cours de la semaine 1 et, pour $n \geqslant 1$, on note $A_n$ l'évènement : « le client achète un melon au cours de la semaine $n$ ». On a ainsi $p\left(A_1\right) = 1$.
-
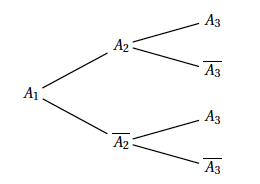
- Reproduire et compléter l'arbre de probabilités ci-dessous, relatif aux trois premières semaines.
- Démontrer que $p\left(A_3\right) = 0,85$.
- Sachant que le client achète un melon au cours de la semaine 3, quelle est la probabilité qu'il en ait acheté un au cours de la semaine 2 ? Arrondir au centième.
Dans la suite, on pose pour tout entier $n \geqslant 1$ : $p_n = P\left(A_n\right)$. On a ainsi $p_1 = 1$.
- Démontrer que, pour tout entier $n \geqslant 1$ : $p_{n+1} = 0,5p_n + 0,4$.
-
- Démontrer par récurrence que, pour tout entier $n \geqslant 1$ : $p_n > 0,8$.
- Démontrer que la suite (p n) est décroissante.
- La suite $\left(p_n\right)$ est-elle convergente ?
- On pose pour tout entier $n \geqslant 1$ : $v_n = p_n - 0,8$.
- Démontrer que $\left(v_n\right)$ est une suite géométrique dont on donnera le premier terme $v_1$ et la raison.
- Exprimer $v_n$ en fonction de $n$. En déduire que, pour tout $n \geqslant 1$, $p_n = 0,8 + 0,2 \times 0,5^{n-1}$.
- Déterminer la limite de la suite $\left(p_n\right)$.
- Vues: 40093
