Baccalauréat S Centres étrangers 11 juin 2018

Page 1 sur 10

 

 

Exercice 1 4 points

Commun à tous les candidats

Dans une usine, on se propose de tester un prototype de hotte aspirante pour un local industriel. Avant de lancer la fabrication en série, on réalise l'expérience suivante : dans un local clos équipé du prototype de hotte aspirante, on diffuse du dioxyde de carbone (CO$_2$) à débit constant. Dans ce qui suit, $t$ est le temps exprimé en minute. À l'instant $t = 0$, la hotte est mise en marche et on la laisse fonctionner pendant $20$ minutes. Les mesures réalisées permettent de modéliser le taux (en pourcentage) de CO$_2$ contenu dans le local au bout de $t$ minutes de fonctionnement de la hotte par l'expression $f(t)$, où $f$ est la fonction définie pour tout réel $t$ de l'intervalle $[0~;~20]$ par : \[f(t) = (0,8t + 0,2)\text{e}^{-0,5t} + 0,03.\] On donne ci-dessous le tableau de variation de la fonction $f$ sur l'intervalle $[0~;~20]$. Ainsi, la valeur $f(0) = 0,23$ traduit le fait que le taux de CO$_2$ à l'instant $0$ est égal à 23 %.
 

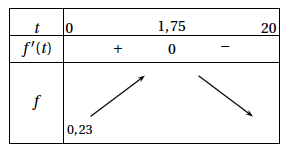
1. Dans cette question, on arrondira les deux résultats au millième.
   1. Calculer $f (20)$.
   2. Déterminer le taux maximal de CO$_2$ présent dans le local pendant l'expérience.
2. On souhaite que le taux de CO$_2$ dans le local retrouve une valeur $V$ inférieure ou égale à $3,5$ %.
   1. Justifier qu'il existe un unique instant $T$ satisfaisant cette condition.
   2. On considère l'algorithme suivant : $$ \begin{array} {|l |}\hline t \gets 1,75 \\ p \gets 0,1 \\ V \gets 0,7 \\ \text{Tant que } V > 0,035 \\ \hspace{0.75cm} t \gets t + p \\ \hspace{0.75cm} V \gets (0,8t + 0,2)\text{e}^{-0,5t} + 0,03 \\ \text{Fin Tant que}\\ \hline \end{array} $$ Quelle est la valeur de la variable $t$ à la fin de l'algorithme ? Que représente cette valeur dans le contexte de l'exercice ?
3. On désigne par $V_m$ le taux moyen ( en pourcentage) de CO$_2$ présent dans le local pendant les Il premières minutes de fonctionnement de la hotte aspirante.
   1. Soit $F$ la fonction définie sur l'intervalle $[0~;~11]$ par : \[F(t) = (-1,6t -3,6)\text{e}^{-0,5t} +0,03t.\] Montrer que la fonction $F$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~11]$.
   2. En déduire le taux moyen $V_m$, valeur moyenne de la fonction $f$ sur l'intervalle $[0~;~11]$. Arrondir le résultat au millième, soit à $0,1$ %.