Baccalauréat S Antilles-Guyane 6 septembre 2018 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (4 points)

Commun à tous les candidats

On considère un cube ABCDEFGH. L'espace est rapporté au repère $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$. La figure est donnée ci-dessous.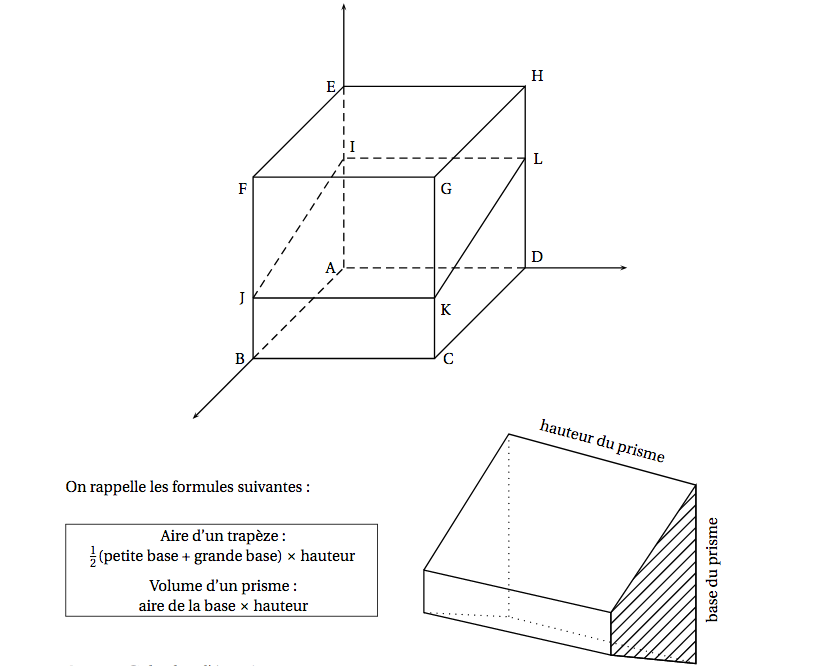

On note $\mathcal{P}_1$ le plan d'équation $4x + 15z - 9 = 0$. La section IJKL du cube ABCDEFGH par le plan $\mathcal{P}_1$ est représentée sur la figure.

1. Déterminer les coordonnées des points I et J.
Le point $I$ a pour coordonnées $(0;0;z)$. Il appartient de plus au plan $\mathscr{P}_1$.
Donc $15z-9=0 \iff z=\dfrac{3}{5}$
Ainsi $I$ a pour coordonnées $(0;0;0,6)$.
$\quad$
Le point $J$ a pour coordonnées $(1,0,z)$.
Il appartient de plus au plan $\mathscr{P}_1$.
Donc $4+15z-9=0 \iff z=\dfrac{1}{3}$.
Le point $J$ a pour coordonnées $\left(1;0;\dfrac{1}{3}\right)$.
$\quad$
2. Le plan $\mathcal{P}_1$ partage le cube en deux prismes. Calculer le volume de chacun de ces deux prismes.
Volume du prisme $BCKJADLI$ :
$\begin{align*} V_1&=\dfrac{(BJ+AI)\times AB}{2}\times BC \\
&=\dfrac{\dfrac{1}{3}+\dfrac{3}{5}}{2}
&=\dfrac{7}{15}\end{align*}$
$\quad$
Volume du prisme $JKGFILHE$ : $V_2=V_{ABCDEFGH}-V_1=1-\dfrac{7}{15}=\dfrac{8}{15}$.
$\quad$
3. Soit M un point du segment [EI]. On cherche un plan $\mathcal{P}_2$ parallèle à $\mathcal{P}_1$ et passant par M qui partage le cube en deux prismes de même volume. Déterminer une équation cartésienne de $\mathcal{P}_2$.
Une équation d’un plan parallèle à $\mathscr{P}_1$ est de la forme $4x+15z-m=0$.
Le point $I’$ a pour coordonnées $(0;0;z)$. Il appartient de plus au plan $\mathscr{P}_2$.
Donc $15z-m=0 \iff z=\dfrac{m}{15}$
Ainsi $I’$ a pour coordonnées $\left(0;0;\dfrac{m}{15}\right)$.
$\quad$
Le point $J’$ a pour coordonnées $(1,0,z)$.
Il appartient de plus au plan $\mathscr{P}_2$.
Donc $4+15z-m=0 \iff z=\dfrac{m-4}{15}$.
Le point $J’$ a pour coordonnées $\left(1;0;\dfrac{m-4}{15}\right)$.
$\quad$
Volume du prisme $BCKJ’ADLI’$ :
$\begin{align*} V’_1&=\dfrac{(BJ’+AI’)\times AB}{2}\times BC \\
&=\dfrac{\dfrac{m-4}{15}+\dfrac{m}{15}}{2}
&=\dfrac{2m-4}{30}\\
&=\dfrac{m-2}{15}\end{align*}$
$\quad$
On veut que :
$\begin{align*} V’_1=\dfrac{1}{2}&\iff \dfrac{m-2}{15}=\dfrac{1}{2} \\
&\iff 2(m-2)=15 \\
&\iff 2m-4=15\\
&\iff 2m=19\\
&\iff m=9,5
\end{align*}$
$\quad$
Une équation de $\mathscr{P}_2$ est donc $4x+15z-9,5=0$.
$\quad$