Baccalauréat S Antilles-Guyane 6 septembre 2018 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

On note $\mathbb{R}$ l'ensemble des nombres réels.

Partie A

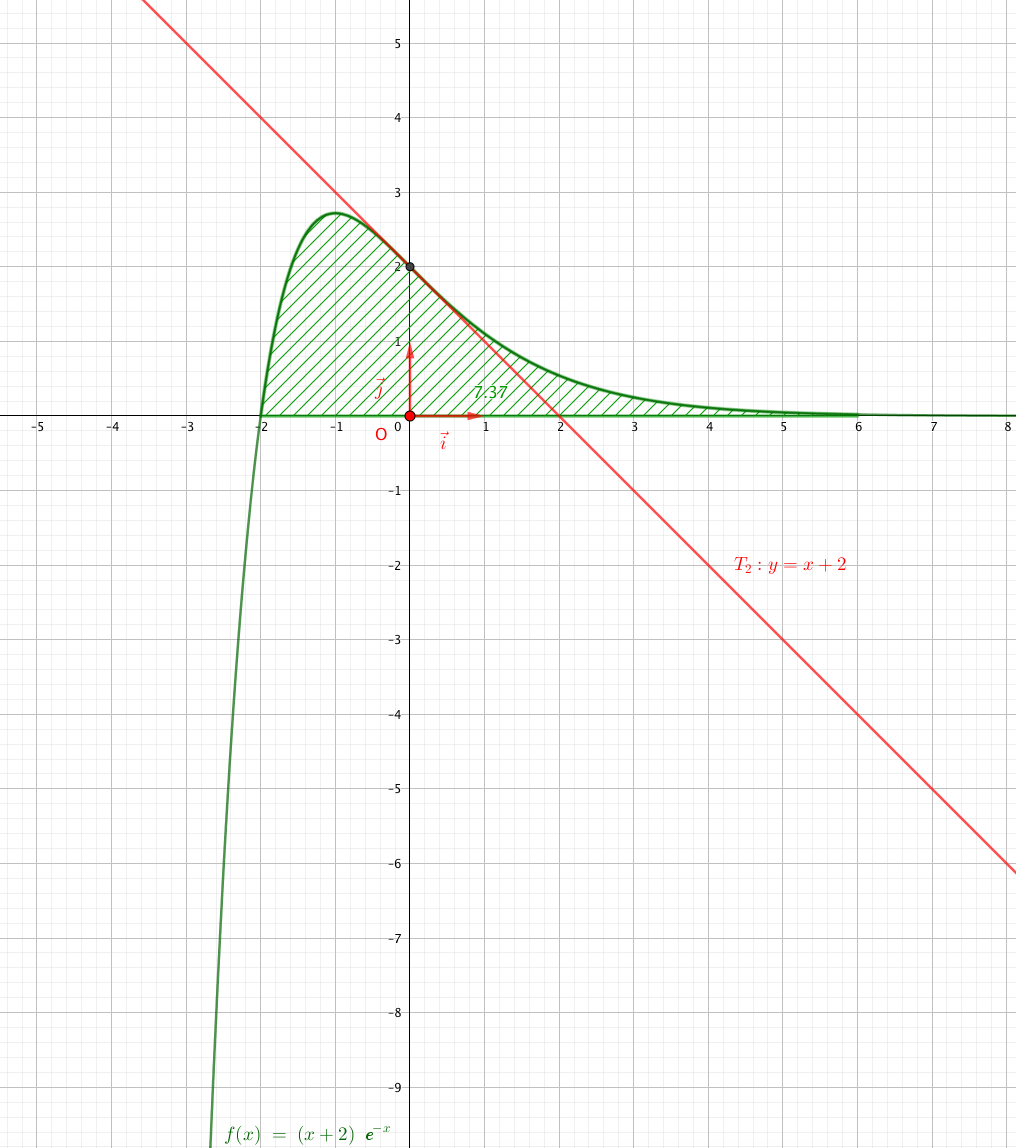
Soit $f_2$ la fonction définie sur $\mathbb{R}$ par \[f_2(x) = (x + 2)\text{e}^{-x}.\] La courbe représentative de $f_2$, notée $\mathcal{C}_2$, est tracée dans un repère orthonormé sur l'ANNEXE à rendre avec la copie.
Aucune justification ni aucun calcul ne sont attendus dans cette partie.

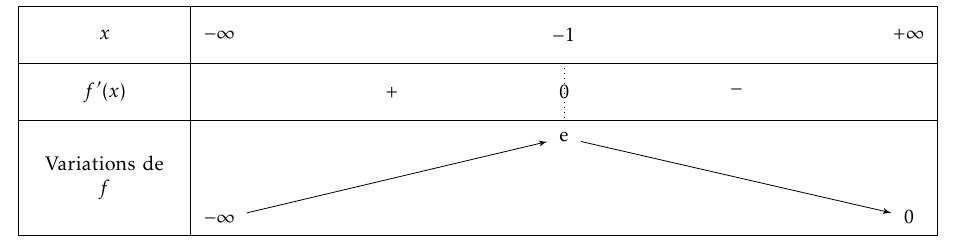
1. Conjecturer les limites de $f_2$ en $- \infty$ et $+ \infty$.
D’après le graphique, il semblerait que $\lim\limits_{x\to -\infty} f_2(x)=-\infty$ et $\lim\limits_{x \to +\infty}f_2(x)=0$.
$\quad$
2. Conjecturer le tableau de variations de $f_2$ à l'aide du graphique.
On peut conjecturer le tableau de variations suivant :


3. Soit $T_2$ la tangente à la courbe $\mathcal{C}_2$ au point d'abscisse $0$. Tracer cette tangente sur l'ANNEXE à rendre avec la copie, puis en conjecturer une équation par lecture graphique.
Il semblerait qu’une équation de $T_2$ soit $y=-x+2$.

4. Sur l'ANNEXE à rendre avec la copie, hachurer un domaine dont l'aire est donnée par l'intégrale \[\displaystyle\int_{-2}^6 f_2(t)\:\text{d}t.\]

 

Partie B

Pour tout réel $m$, on note $f_m$ la fonction définie sur $\mathbb{R}$ par \[f_m(x) = (x + m)\text{e}^{- x}\] et $\mathcal{C}_m$ sa courbe représentative dans un repère orthonormé.

1. Calculer les limites de $f_m$ en $- \infty$ et $+ \infty$.
$\lim\limits_{x \to -\infty} x+m=-\infty$
Or $\lim\limits_{x \to -\infty} -x=+\infty$ et $\lim\limits_{X \to +\infty} \text{e}^X=+\infty$ donc $\lim\limits_{x \to -\infty} \text{e}^{-x}=+\infty$.
Donc $\lim\limits_{x \to -\infty} f_m(x)=-\infty$.
$\quad$
On a $f_m(x)=x\text{e}^{-x}+m\text{e}^{-x}$
Or $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$ donc $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$.
De plus $\lim\limits_{x \to +\infty} -x=+\infty$ et $\lim\limits_{X \to +\infty} X\text{e}^X=0$ donc $\lim\limits_{x \to +\infty} x\text{e}^{-x}=0$.
Par conséquent $\lim\limits_{x \to +\infty} f_m(x)=0$.

2. On admet que $f_m$ est dérivable sur $\mathbb{R}$ et on note $f'_m$ sa dérivée. Montrer que, pour tout réel $x$, $f'_m(x) = (-x - m + 1)\text{e}^{- x}$.
Pour tout réel $x$ on a :
$\begin{align*} {f_m}'(x)&=\text{e}^{-x}-(x+m)\text{e}^{-x} \\
&=(-x-m+1)\text{e}^{-x} \end{align*}$
$\quad$
3. En déduire les variations de $f_m$ sur $\mathbb{R}$.
La fonction exponentielle est strictement positive.
Par conséquent le signe de ${f_m}'(x)$ ne dépend que de celui de $-x-m+1$.
Or $-x-m+1=0 \iff x=1-m$ et $-x-m+1>0 \iff x<1-m$.
La fonction $f_m$ est donc croissante sur l’intervalle $]-\infty;1-m]$ et décroissante sur l’intervalle $[1-m;+\infty[$.
$\quad$
4. 1. Pour tout réel $m$, on note $T_m$ la tangente à la courbe $\mathcal{C}_m$ au point d'abscisse $0$. Démontrer que $T_m$ a pour équation réduite $y = (1 - m)x + m$.
   2. a. Une équation de $T_m$ est $y={f_m}'(0)x+f_m(0)$
      Soit $y=(-m+1)x+m$
      $\quad$
   3. Démontrer que toutes les droites $T_m$ passent par un même point dont on précisera les coordonnées.
   Il semblerait que le point de coordonnées $(1;1)$ appartienne à toutes les droites $T_m$.
   Vérifions cette conjecture : $(1-m)\times 1+m=1-m+m=1$.
   Toutes les droites $T_m$ passent donc par le point de coordonnées $(1;1)$.
   $\quad$
5. Étudier le signe de $f_m(x)$ pour tout réel $x$.
La fonction exponentielle est strictement positive. Le signe de $f_m(x)$ ne dépend donc que de celui de $x+m$.
Or $x+m=0\iff x=-m$ et $x+m>0 \iff x>-m$.
Ainsi :
– sur l’intervalle $]-\infty;-m[$, on a $f_m(x)<0$;
– on a $f_m(-m)=0$;
– sur l’intervalle $]-m;+\infty[$, on a $f_m(x)>0$.
$\quad$
6. On admet que la fonction $F_2$ définie sur $\mathbb{R}$ par $F_2(x) = -(x + 3)\text{e}^{- x}$ est une primitive de $f_2$ sur $\mathbb{R}$.
   1. Déterminer, en fonction de $x$, l'expression de \[\displaystyle\int_{-2}^x f_2(t)\:\text{d}t.\]
   Pour tout réel $x$ on a :
   $\displaystyle \begin{align*} \int_{-2}^x f_2(t)\:\text{d}t &=F_2(x)-F_2(-2) \\
   &=-(x+3)\text{e}^{-x}+\text{e}^{2} \end{align*}$
   $\quad$
   
   2. En déduire la valeur de \[\displaystyle\lim_{x \to + \infty} \int_{-2}^x f_2(t)\:\text{d}t.\]
   On a ainsi $\displaystyle \int_{-2}^x f_2(t)\:\text{d}t = -f_3(x)+\text{e}^{2}$
   Or $\lim\limits_{x \to +\infty} f_3(x)=0$ donc $\displaystyle \lim\limits_{x \to +\infty} \int_{-2}^x f_2(t)\:\text{d}t=\text{e}^2$.
   $\quad$

Annexe