Baccalauréat STI2D et STL/SPCL - Polynésie 21 juin 2018
Exercice 1 4 points
Cet exercice est composé de deux parties indépendantes.
Partie A
Pour chacune des questions suivantes, une seule réponse est correcte.
Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse choisie.
Aucune justification n'est demandée.
Une bonne réponse rapporte $0,5$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse ne rapportent ni n'enlèvent aucun point.
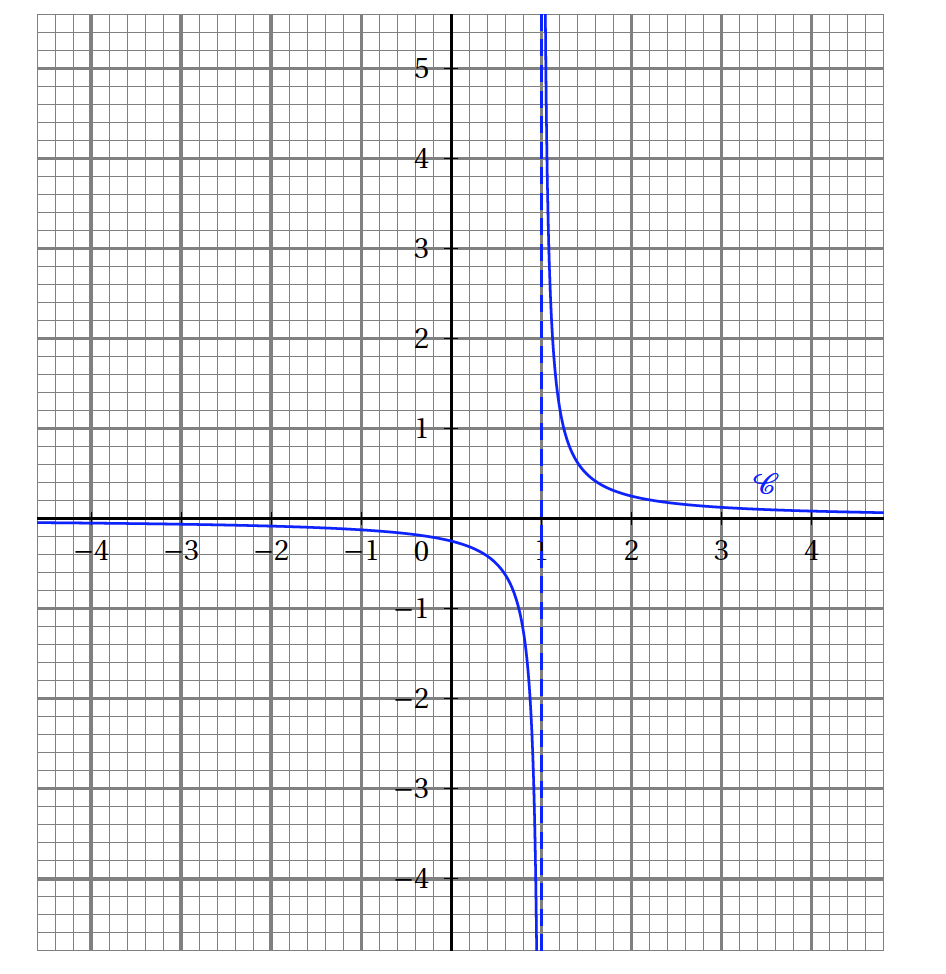
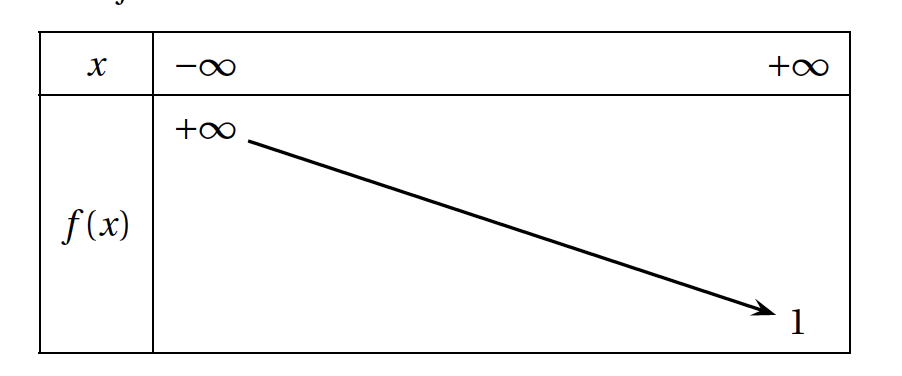
- On donne ci-dessous la représentation graphique $\mathcal{C}$ d'une fonction$f$ définie sur $]-\infty~;~1[ \cup ]1~;~+\infty[$.
- $\displaystyle\lim_{x \to +\infty} f(x)=1$
- $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
- $\displaystyle\lim_{\substack{x \to 1 \\ x > 1}} f(x)= -\infty$
- $\displaystyle\lim_{x\to -\infty} f(x)= -\infty$
- Une solution $g$ de l'équation différentielle $y''+9y=0$ vérifiant $g(0)=1$ est définie sur $\mathbb R$ par:
- $g(t)= \cos\left (9t\right ) + \sin \left (9t\right )$
- $g(t)= 4\,\cos \left (3t\right ) - 3$
- $g(t)= \cos\left (3t\right ) + \sin \left (3t\right )$
- $g(t)= 2\, \cos\left (3t\right ) - \sin \left (3t\right )$
- L'équation $\ln\left (x-2\right ) = -2$ admet pour solution dans $\mathbb R$:
- $0$
- $2+\text{e}^{-2}$
- $2,14$
- $2-\text{e}^{2}$
- La dérivée de la fonction $h$ définie sur $\mathbb R$ par $h(x)=x\text{e}^{-2x}$ est la fonction $h'$ définie sur $\mathbb R$ par:
- $h'(x)=\text{e}^{-2x}$
- $h'(x)=-2\text{e}^{-2x}$
- $h'(x)=-2x\text{e}^{-2x}$
- $h'(x)=\left (1-2x\right )\text{e}^{-2x}$
Partie B
Le plan complexe est muni d'un repère orthonormé $\left(\text{O}~;~\vec{u},~\vec{v}\right)$. On note $ \text{i}$ le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$. On considère les points A, B et C du plan complexe d'affixes respectives $z_{\mathrm A}$, $z_{\mathrm B}$ et $z_{\mathrm C}$: \[z_{\mathrm A} = \dfrac{\sqrt{2} + \text{i} \sqrt{2}}{ \text{i}} \hspace{2cm} z_{\mathrm B} = 2 \text{e}^{ \text{i} \frac{\pi}{3}} \hspace{2cm} z_{\mathrm C} = -2 \text{i}\text{e}^{- \text{i}\frac{\pi}{6}}\] Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier les réponses choisies.Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l'évaluation.
Une réponse non justifiée ne rapporte aucun point.
- Affirmation 1: La forme algébrique de $z_{\mathrm{A}}$ est $\sqrt{2}- \text{i}\sqrt{2}$.
- Affirmation 2: Un argument de $z_{\mathrm{C}}$ est $\dfrac{\pi}{6}$.
- Affirmation 3: Les points A, B et C sont sur un même cercle de centre O.
- Affirmation 4: O est le milieu du segment [BC].
Correction de l'exercice 1 (4 points)
Cet exercice est composé de deux parties indépendantes.
Partie A
Pour chacune des questions suivantes, une seule réponse est correcte.
Recopier sur la copie le numéro de la question et la lettre correspondant à la réponse choisie.
Aucune justification n'est demandée.
Une bonne réponse rapporte $0,5$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse ne rapportent ni n'enlèvent aucun point.
- On donne ci-dessous la représentation graphique $\mathcal{C}$ d'une fonction$f$ définie sur $]-\infty~;~1[ \cup ]1~;~+\infty[$.
- $\displaystyle\lim_{x \to +\infty} f(x)=1$
- $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
- $\displaystyle\lim_{\substack{x \to 1 \\ x > 1}} f(x)= -\infty$
- $\displaystyle\lim_{x\to -\infty} f(x)= -\infty$
 Par lecture graphique, on a : $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
Par lecture graphique, on a : $\displaystyle\lim_{\substack{x \to 1 \\ x < 1}} f(x)= -\infty$
- Une solution $g$ de l'équation différentielle $y''+9y=0$ vérifiant $g(0)=1$ est définie sur $\mathbb R$ par:
- $g(t)= \cos\left (9t\right ) + \sin \left (9t\right )$
- $g(t)= 4\,\cos \left (3t\right ) - 3$
- $g(t)= \cos\left (3t\right ) + \sin \left (3t\right )$
- $g(t)= 2\, \cos\left (3t\right ) - \sin \left (3t\right )$
L'équation différentielle $y″+9y=0$ est du type $y"+\omega ^2y=0$ où $\omega=3$. - L'équation $\ln\left (x-2\right ) = -2$ admet pour solution dans $\mathbb R$:
- $0$
- $2+\text{e}^{-2}$
- $2,14$
- $2-\text{e}^{2}$
$\ln x-2=-2\iff x-2=e^{-2}\iff x=2+e^{-2}$ - La dérivée de la fonction $h$ définie sur $\mathbb R$ par $h(x)=x\text{e}^{-2x}$ est la fonction $h'$ définie sur $\mathbb R$ par:
- $h'(x)=\text{e}^{-2x}$
- $h'(x)=-2\text{e}^{-2x}$
- $h'(x)=-2x\text{e}^{-2x}$
- $h'(x)=\left (1-2x\right )\text{e}^{-2x}$
$h$ est dérivable comme somme de deux fonctions dérivables. $h=u v ,$ d'où $f'=u'v+v'u $ avec pour tout réel $x$: $\left\{ \begin{array}{l} u(x)~ =x \\ v(x)~ = \text{e}^{-2x}\end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = 1 \\ v'(x)~ = -2\text{e}^{-2x}\end{array}\right.$ $$ \begin{array}{cl} h'(x)& =1\times \text{e}^{-2x}+\left (-2\text{e}^{-2x}\right )\times x\\ & = \text{e}^{-2x}-2x\text{e}^{-2x} \\ &= \text{e}^{-2x}\left (1-2x\right ) \end{array} $$ La bonne réponse est d.
Les solutions de l'équation différentielle $y″+9y=0$ sont les fonctions définies $f$ sur $\mathbb R$ par $f(t)=A\cos\left (3t\right ) +B \sin \left (3t\right )$ où $A$ et $B$ sont deux constantes réelles.
La condition $g(0)=1$ équivaut à $A=1$.
Ainsi, une solution $g$ de cette l'équation différentielle vérifiant $g(0)=1$ est définie sur $\mathbb R$ par $f(t)=\cos\left (3t\right ) + \sin \left (3t\right )$
La bonne réponse est b.
Partie B
Le plan complexe est muni d'un repère orthonormé $\left(\text{O}~;~\vec{u},~\vec{v}\right)$. On note $ \text{i}$ le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$. On considère les points A, B et C du plan complexe d'affixes respectives $z_{\mathrm A}$, $z_{\mathrm B}$ et $z_{\mathrm C}$: \[z_{\mathrm A} = \dfrac{\sqrt{2} + \text{i} \sqrt{2}}{ \text{i}} \hspace{2cm} z_{\mathrm B} = 2 \text{e}^{ \text{i} \frac{\pi}{3}} \hspace{2cm} z_{\mathrm C} = -2 \text{i}\text{e}^{- \text{i}\frac{\pi}{6}}\] Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse et justifier les réponses choisies.Toute trace de recherche, même incomplète ou non fructueuse, sera prise en compte dans l'évaluation.
Une réponse non justifiée ne rapporte aucun point.
- Affirmation 1: La forme algébrique de $z_{\mathrm{A}}$ est $\sqrt{2}- \text{i}\sqrt{2}$. $$ \begin{array}{cl} z_{\mathrm A} &= \dfrac{\sqrt{2} + \text{i} \sqrt{2}}{ \text{i}} \\ & = \dfrac{\left ( \sqrt{2} + \text{i} \sqrt{2} \right )\times ( -\text{i} )}{ \text{i}\times (- \text{i} )} \\ &= \dfrac{\left ( -\text{i}\sqrt{2} - \text{i} ^2\sqrt{2} \right )}{ 1} \\ &=\sqrt{2}-\text{i}\sqrt{2} \end{array} $$ L'affirmation 1 est donc vraie.
- Affirmation 2: Un argument de $z_{\mathrm{C}}$ est $\dfrac{\pi}{6}$. $-2\text{i}\text{e}^{- \text{i}\frac{\pi}{6}}$ n'est pas une forme exponentielle d'un nombre complexe. Comme $\text{e}^{- \text{i}\frac{\pi}{2}}=- \text{i}$, on en déduit : $$ \begin{array}{cl} z_{\mathrm C} &= -2\text{i}\text{e}^{- \text{i}\frac{\pi}{6}} \\ & = 2 \text{e}^{- \text{i}\frac{\pi}{2}} \text{e}^{- \text{i}\frac{\pi}{6}} \\ &= 2 \text{e}^{- \text{i}(-\frac{\pi}{2}-\frac{\pi}{6})} \\ &2 \text{e}^{- \text{i} \frac{2\pi}{3} } \end{array} $$ L'affirmation 2 est fausse : un argument de $z_{\mathrm C}$ est $-\frac{2\pi}{3}$.
- Affirmation 3: Les points A, B et C sont sur un même cercle de centre O. Le module du nombre complexe $z_{\mathrm A}=\sqrt 2-\text{i}\sqrt 2$ est : $\rvert z_{\mathrm A}\rvert=\sqrt{\sqrt 2^2+\sqrt 2^2}=\sqrt 4=2$.
- Affirmation 4: O est le milieu du segment [BC]. $$ \begin{array}{cl} \left (\vec{OC} ;\vec{OB}\right )&=arg\left (\dfrac{z_{\mathrm B}}{z_{\mathrm C}}\right ) \\ &= arg\left( z_{\mathrm B} \right ) -arg\left ( z_{\mathrm C} \right ) \\ & =\frac{\pi}{3} -\left ( -\frac{2\pi}{3} \right )\\ &=\pi\\ \end{array} $$ Comme $\left (\vec{OC} ;\vec{OB}\right )=\pi$, les vecteurs $\vec{OC}$ et $\vec{OB}$ sont colinéaires de sens opposé.
Le module du nombre complexe $z_{\mathrm B}=2\text{e}^{ \text{i}\frac{\pi}{3}} $ est $\rvert z_{\mathrm B}\rvert =2$ et, le module du nombre complexe $z_{\mathrm C}= 2 \text{e}^{- \text{i}( \frac{2\pi}{3}}$ est $\rvert z_{\mathrm C}\rvert =2$
L'affirmation 3 est vraie : $\rvert z_{\mathrm A}\rvert = \rvert z_{\mathrm B}\rvert =\rvert z_{\mathrm C}\rvert =2$ donc les points A, B et C sont sur le cercle de centre O et de rayon 2.
Par ailleurs $\rvert z_{\mathrm B}\rvert =\rvert z_{\mathrm C}\rvert =2$, donc $OB=OC=2$.
L'affirmation 4 est vraie :O est le milieu du segment [BC].
Exercice 2 6 points
Les deux parties de l'exercice sont indépendantes.
Partie A
Dans cette partie on s'intéresse à l'évolution, depuis 2010, du nombre de véhicules « 100% électriques » en France. Le 24 mars 2017, l'association nationale pour le développement de la mobilité électrique (Avere-France) a publié l'article suivant:
La France célèbre son 100ieme véhicule
« 100% électrique », une première en Europe
Jeudi 23 mars, le marché français des véhicules particuliers et utilitaires « 100% électrique » a franchi le cap des $100\;000$ immatriculations cumulées depuis 2010, date de lancement de la nouvelle génération de véhicules électriques. La France devient alors le premier pays européen à atteindre un tel parc de véhicules avec zéro émission. 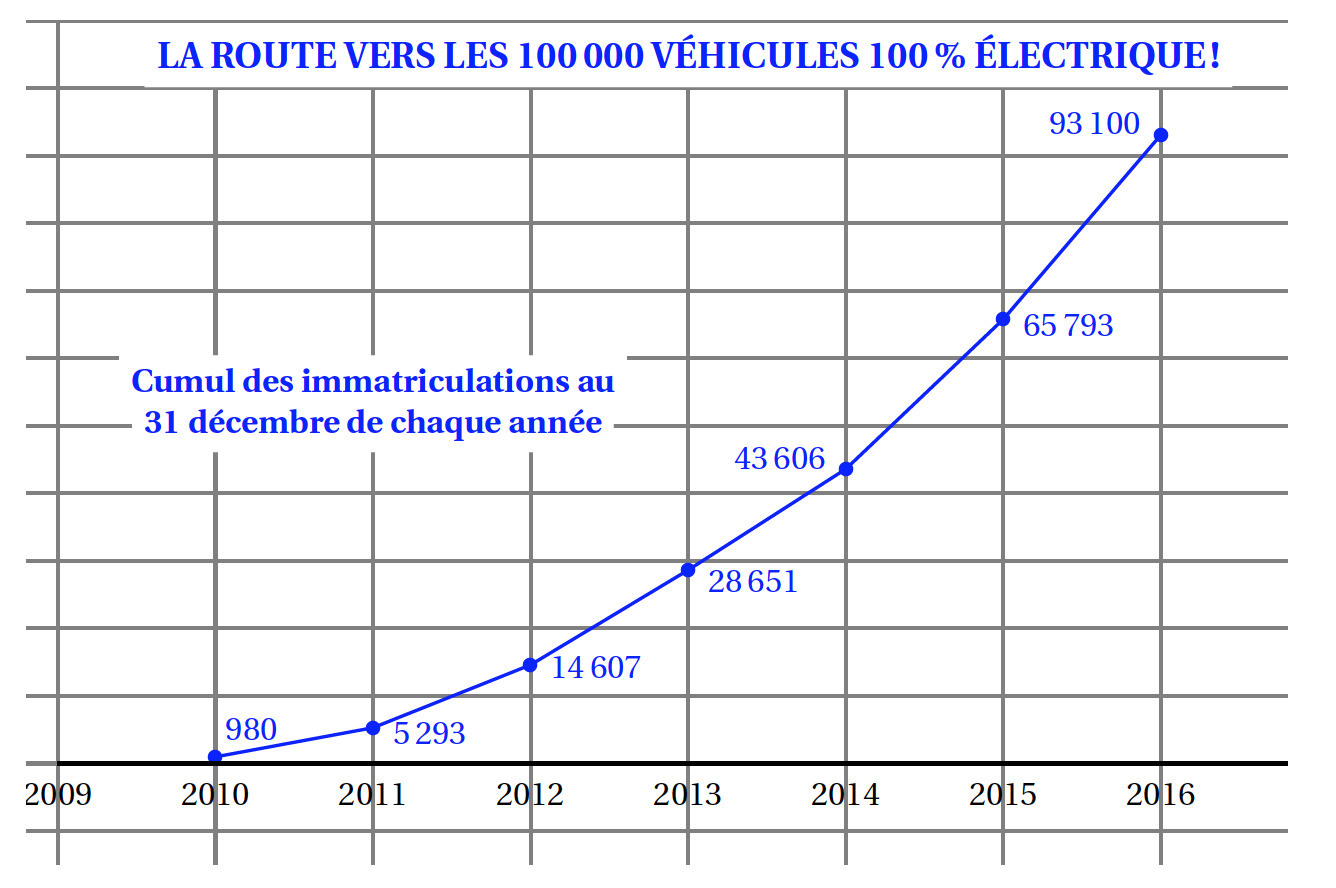
Dans ce contexte économique et environnemental, l'Avere-France estime qu'à l'horizon 2020, la France devrait compter plus de $350\;000$ véhicules « 100% électrique » immatriculés.
D'après l'association Avere-France
La lecture du graphique précédent permet, par exemple, de dire qu'au 31 décembre 2015, il y avait en tout $65\;793$ véhicules « 100% électrique » immatriculés.
- Déterminer le pourcentage d'augmentation, entre le 31 décembre 2015 et le 31 décembre 2016, du nombre de véhicules « 100% électrique » immatriculés en France. Arrondir le résultat à 1%.
-
- Déterminer le nombre de véhicules « 100% électrique » en France au 31 décembre 2017.
- Déterminer la nature de la suite $(u_n)$.
- L'affirmation de l'association Avere-France figurant à la fin de l'article est-elle validée par le modèle proposé? Justifier la réponse.
- À l'aide d'un algorithme, on souhaite estimer l'année au cours de laquelle le nombre de véhicules « 100% électrique » immatriculés en France dépassera $1000\;000$ avec ce modèle.
- Recopier et compléter l'algorithme suivant afin qu'il réponde au problème.
$$\begin{array}{|l|} \hline n \leftarrow 0 \\ u \leftarrow 93\;100 \\ \text{Tant que } \cdots\\ \hspace{1cm} n \leftarrow \cdots \\ \hspace{1cm} u \leftarrow \cdots\\ \text{Fin Tant que}\\ \hline \end{array}$$ - Laquelle des variables $n$ ou $u$ est-il utile d'afficher après l'exécution de cet algorithme pour répondre au problème?
- Quelle est la valeur de cette variable?
- Interpréter cette valeur dans le contexte de l'exercice.
- Recopier et compléter l'algorithme suivant afin qu'il réponde au problème.
On suppose qu'à partir de l'année 2017, l'augmentation annuelle de véhicules « 100% électrique » immatriculés en France sera constante et égale à 40%. Dans le cadre de ce modèle, pour tout entier naturel $n$, on note $u_n$ une estimation du nombre de véhicules « 100% électrique » immatriculés en France au 31 décembre de l'année $2016+n$. Ainsi on a $u_0 = 93\;100 $.
Partie B
Une usine fabrique des batteries Lithium-Ion, garanties 4 ans, nécessaires au fonctionnement des véhicules « 100% électrique ». La durée de vie moyenne d'une telle batterie s'élève à 7 ans. On admet que la variable aléatoire $T$ qui, à une batterie Lithium-Ion prélevée au hasard dans le stock de l'usine, associe sa durée de vie, exprimée en années, suit la loi exponentielle de paramètre $\lambda$.
- Déterminer la valeur exacte de $\lambda$.
- Pour la suite, on prendra $\lambda = 0,143$.
- Déterminer la probabilité qu'une batterie Lithium-Ion soit encore en état de fonctionnement au bout de 8 ans. On donnera une valeur approchée à $10^{-3}$ près.
- Déterminer la probabilité qu'une batterie Lithium-Ion tombe en panne avant la fin de la garantie. On donnera une valeur approchée à $10^{-3}$ près.
- Déterminer le réel $t_0$ tel que $P(T>t_0)=0,75$. On donnera la valeur exacte et la valeur arrondie à l'unité. Interpréter le résultat dans le contexte de l'exercice.
Correction de l'exercice 2 (5 points)
Les deux parties de l'exercice sont indépendantes.
Partie A
Dans cette partie on s'intéresse à l'évolution, depuis 2010, du nombre de véhicules « 100% électriques » en France. Le 24 mars 2017, l'association nationale pour le développement de la mobilité électrique (Avere-France) a publié l'article suivant:
La France célèbre son 100ieme véhicule
« 100% électrique », une première en Europe
Jeudi 23 mars, le marché français des véhicules particuliers et utilitaires « 100% électrique » a franchi le cap des $100\;000$ immatriculations cumulées depuis 2010, date de lancement de la nouvelle génération de véhicules électriques. La France devient alors le premier pays européen à atteindre un tel parc de véhicules avec zéro émission. 
Dans ce contexte économique et environnemental, l'Avere-France estime qu'à l'horizon 2020, la France devrait compter plus de $350\;000$ véhicules « 100% électrique » immatriculés.
D'après l'association Avere-France
La lecture du graphique précédent permet, par exemple, de dire qu'au 31 décembre 2015, il y avait en tout $65\;793$ véhicules « 100% électrique » immatriculés.
- Déterminer le pourcentage d'augmentation, entre le 31 décembre 2015 et le 31 décembre 2016, du nombre de véhicules « 100% électrique » immatriculés en France. Arrondir le résultat à 1%. $$\left (\dfrac{93100}{65793}-1\right )\times 100\approx 41,5$$ Entre le 31 décembre 2015 et le 31 décembre 2016, le nombre de véhicules « 100 % électrique » immatriculés en France a augmenté d'environ 42 %.
-
- Déterminer le nombre de véhicules « 100% électrique » en France au 31 décembre 2017. $$u_1=93100\times \left(1+\dfrac{40}{100}\right)=93100\times 1,4=130340$$
- Déterminer la nature de la suite $(u_n)$. Le coefficient multiplicateur associé à une augmentation de 40 % est égal à 1,4.
- L'affirmation de l'association Avere-France figurant à la fin de l'article est-elle validée par le modèle proposé? Justifier la réponse. $\left(u_n \right)$ est une suite géométrique de raison $q=1,4$ et de premier terme $u_0=93100$ donc pour tout entier naturel $n, u_n=93100\times 1,4^n$.
Pour tout entier naturel $n$, on a $u_{n+1}=1,4u_n$. Par conséquent, $\left(u_n \right)$ est une suite géométrique de raison $q=1,4$.
On en déduit que : $$u_4=93100\times 1,4^4\approx 357653$$ Selon ce modèle, il devrait y avoir plus de 357 600 véhicules « 100 % électrique » immatriculés en France au 31 décembre de l'année 2020. Ce résultat est conforme avec l'estimation de l'association Avere-France. - À l'aide d'un algorithme, on souhaite estimer l'année au cours de laquelle le nombre de véhicules « 100% électrique » immatriculés en France dépassera $1000\;000$ avec ce modèle.
- Recopier et compléter l'algorithme suivant afin qu'il réponde au problème.
$$\begin{array}{|l|} \hline n \leftarrow 0 \\ u \leftarrow 93\;100 \\ \text{Tant que } \cdots\\ \hspace{1cm} n \leftarrow \cdots \\ \hspace{1cm} u \leftarrow \cdots\\ \text{Fin Tant que}\\ \hline \end{array}$$ $$\begin{array}{|l|} \hline n \leftarrow 0 \\ u \leftarrow 93\;100 \\ \text{Tant que }u < 1000000\\ \hspace{1cm} n \leftarrow n+1 \\ \hspace{1cm} u \leftarrow 1,4\times u\\ \text{Fin Tant que}\\ \hline \end{array}$$
- Laquelle des variables $n$ ou $u$ est-il utile d'afficher après l'exécution de cet algorithme pour répondre au problème? Il convient d'afficher la variable $n$ qui contient le nombre d'années depuis 2016 pour que le nombre de véhicules « 100 % électrique » immatriculés en France dépasse 1 000 000.
- Quelle est la valeur de cette variable? pour tout entier naturel $n, u_n=93100\times 1,4^n$ $$\begin{array}{rll} u_n <1 000 000 & \iff 93100\times 1,4^n <1 000 000. &\\ & \iff 1,4^n <\frac{1 000 000}{93100}&\\ &\iff 1,4^n < \frac{10 000}{931}&\\ &\iff \ln\left (1,4^n\right ) <\ln \left (\frac{10 000}{931}\right )& \ln \text{est strictement croissante sur } ]0;+\infty[\\ &\iff n\ln\left (1,4 \right ) <\ln \left ( \frac{10 000}{931}\right )& \text{ car } \ln\left (a^n \right )=n\ln a\\ &\iff n< \dfrac{\ln \left (\frac{10 000}{931}\right )}{\ln\left (1,4 \right )}&\text{ car } 1,4 >1 \text{ donc } \ln\left (1,4 \right ) >0\\ \end{array}$$ Grâce à une calculatrice, on obtient $\dfrac{\ln \left (\frac{10 000}{931}\right )}{\ln\left (1,4 \right )} \approx 7,06$.
- Interpréter cette valeur dans le contexte de l'exercice. Selon ce modèle, c'est en 2024 que le nombre de véhicules « 100 % électrique » immatriculés en France dépassera 1 000 000.
donc le plus petit entier $n$ solution de l'inéquation $u_n>1000000$ est $n=8$.
La valeur de la variable $n$ obtenue à la fin de l'execution de l'algorithme est $n=8$. - Recopier et compléter l'algorithme suivant afin qu'il réponde au problème.
On suppose qu'à partir de l'année 2017, l'augmentation annuelle de véhicules « 100% électrique » immatriculés en France sera constante et égale à 40%. Dans le cadre de ce modèle, pour tout entier naturel $n$, on note $u_n$ une estimation du nombre de véhicules « 100% électrique » immatriculés en France au 31 décembre de l'année $2016+n$. Ainsi on a $u_0 = 93\;100 $.
Partie B
Une usine fabrique des batteries Lithium-Ion, garanties 4 ans, nécessaires au fonctionnement des véhicules « 100% électrique ». La durée de vie moyenne d'une telle batterie s'élève à 7 ans. On admet que la variable aléatoire $T$ qui, à une batterie Lithium-Ion prélevée au hasard dans le stock de l'usine, associe sa durée de vie, exprimée en années, suit la loi exponentielle de paramètre $\lambda$.
- Déterminer la valeur exacte de $\lambda$. L'espérance mathématique de la variable $T $est $E(T)=\dfrac{1}{\lambda} $ d'où : $$\dfrac{1}{\lambda}=7 \iff \lambda \dfrac{1}{7}$$ $T $suit une loi exponentielle de paramètre $\lambda \dfrac{1}{7}$.
- Pour la suite, on prendra $\lambda = 0,143$.
- Déterminer la probabilité qu'une batterie Lithium-Ion soit encore en état de fonctionnement au bout de 8 ans. On donnera une valeur approchée à $10^{-3}$ près. La densité de la variable aléatoire $T$ suivant une loi exponentielle de paramètre $\lambda =0,143$ est la fonction $f$ définie pour tout réel $t$ de l'intervalle $[0;+\infty[ $ par $f(t)=0,143 =0,143e^{-0,143t}$ d'où : $$ \begin{array}{cl} P(T\geq 8) & 1-P(T<8)\\ &= 1- \displaystyle \int_0^8 0,143e^{-0,143t}\; dt \\ & =1-\left [ -e^{-0,143t} \right ]_0^8\\ &=1- \left (-e^{-0,143\times 8} -(-1)\right ) \\ &= e^{-1,144}\\ &\approx 0,319 \end{array} $$ La probabilité qu'une batterie Lithium-Ion soit encore en état de fonctionnement au bout de 8 ans est $P(T\geq 8) \approx 0,319$.
- Déterminer la probabilité qu'une batterie Lithium-Ion tombe en panne avant la fin de la garantie. On donnera une valeur approchée à $10^{-3}$ près. $$ \begin{array}{cl} P(T\leq 4) & = \displaystyle \int_0^4 0,143e^{-0,143t}\; dt \\ & = \left [ -e^{-0,143t} \right ]_0^4\\ &= \left (-e^{-0,143\times 4} -(-1)\right ) \\ &= 1- e^{-0,572}\\ &\approx 0,436 \end{array} $$ La probabilité qu'une batterie Lithium-Ion tombe en panne avant la fin de la garantie est $P(T\leq 4 ) \approx 0,436$.
- Déterminer le réel $t_0$ tel que $P(T>t_0)=0,75$. On donnera la valeur exacte et la valeur arrondie à l'unité. Interpréter le résultat dans le contexte de l'exercice. $$ \begin{array}{cl} P(T\geq t_0) =0,75&\iff 1-P(T < t_0)=0,75\\ &\iff P(T< t_0)=0,25\\ &\iff \displaystyle \int_0^ {t_0} 0,143e^{-0,143t}\; dt =0,25 \\ &\iff \left [ -e^{-0,143t} \right ]_0^{t_0}=0,25\\ &\iff \left (-e^{-0,143\times t_0} -(-1)\right ) =0,25 \\ &\iff 1- e^{-0,143\times t_0} =0,25 \\ &\iff e^{-0,143\times t_0} =0,75 \\ &\iff -0,143t_0=\ln(0,75) \\ &\iff t_0= \dfrac{\ln(0,75)}{-0,143}\\ &\textbf{ soit} t_0\approx 2 \end{array} $$ La probabilité qu'une batterie Lithium-Ion fonctionne plus de deux ans est égale à 0,75.
Exercice 3 4 points
Dans cet exercice, tous les résultats seront arrondis au millième.
Une entreprise assure la maintenance d'un parc de 75 ascenseurs qui fonctionnent de façon indépendante.
Partie A
On considère dans cette partie que la probabilité qu'un ascenseur du parc tombe en panne un jour donné est $0,08$. On note $X$ la variable aléatoire prenant pour valeur le nombre d'ascenseurs qui tombent en panne un jour donné.
-
- Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.
- Calculer la probabilité que 5 ascenseurs tombent en panne un jour donné.
- Calculer la probabilité qu'au moins 5 ascenseurs tombent en panne un jour donné.
- Déterminer l'espérance mathématique de la variable aléatoire $X$.
- On appelle $Y$ la variable aléatoire qui suit la loi normale d'espérance $\mu=6$ et d'écart-type $\sigma=2,349$. On décide d'approcher la loi de $X$ par la loi de $Y$. En utilisant cette nouvelle loi, déterminer la probabilité que:
- entre 5 et 10 ascenseurs tombent en panne un jour donné.
- plus de 10 ascenseurs tombent en panne un jour donné.
Partie B
Depuis quelques temps, l'entreprise constate de nombreuses pannes parmi les 75 ascenseurs. Ainsi, sur une période de 30 jours, il a été relevé 263 pannes en tout. L'entreprise doit-elle remettre en cause, au seuil de 95%, le modèle selon lequel la probabilité qu'un ascenseur tombe en panne un jour donné est $0,08$? Justifier la réponse.
Correction de l'exercice 3 (5 points)
Dans cet exercice, tous les résultats seront arrondis au millième.
Une entreprise assure la maintenance d'un parc de 75 ascenseurs qui fonctionnent de façon indépendante.
Partie A
On considère dans cette partie que la probabilité qu'un ascenseur du parc tombe en panne un jour donné est $0,08$. On note $X$ la variable aléatoire prenant pour valeur le nombre d'ascenseurs qui tombent en panne un jour donné.
-
- Justifier que $X$ suit une loi binomiale dont on précisera les paramètres. On répète 75 fois, de façon indépendante,l'expérience \og On choisit au hasard un ascenceur parmi les 75 du parc . \fg qui comporte 2 issues :
- Calculer la probabilité que 5 ascenseurs tombent en panne un jour donné. À l'aide de la calculatrice, $P(X=5)=\binom{75}{5}\times \left(0,08\right)^5\times\left( 0,92\right)^{70}\approx 0,165$ .
- Calculer la probabilité qu'au moins 5 ascenseurs tombent en panne un jour donné. On calcule : $P(X\geq 5)=1-P(X <5)=1-P(X\leq 4)$.
- Déterminer l'espérance mathématique de la variable aléatoire $X$. Comme $X$ suit une loi binomiale, son espérance mathématique est $E(X)=np=75\times 0.08=6$.
-
« l'ascenseur du parc tombe en panne un jour donné » considéré comme succès, de probabilité $p=0,08$
« l'ascenseur du parc ne tombe pas en panne un jour donné » considéré comme échec, de probabilité $q=1-p=0,92$
Pour tout entier $k$ où $0\leq k\leq 75$, on a $$P(X=k)=\binom{75}{k}\times \left(0,08\right)^k\times\left( 0,92\right)^{75-k}$$2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Arrondie au millième près, la probabilité que 5 ascenseurs tombent en panne un jour donné est 0,165.2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Ainsi $P(X\geq 5)\approx 1-0.274\approx 0.726$
Arrondie au millième près, la probabilité qu'au moins 5 ascenseurs tombent en panne un jour donné est 0,726. - On appelle $Y$ la variable aléatoire qui suit la loi normale d'espérance $\mu=6$ et d'écart-type $\sigma=2,349$. On décide d'approcher la loi de $X$ par la loi de $Y$. En utilisant cette nouvelle loi, déterminer la probabilité que:
- entre 5 et 10 ascenseurs tombent en panne un jour donné. Avec la calculatrice, on trouve $P(5\leq Y\leq 10)\approx 0,621$.
- plus de 10 ascenseurs tombent en panne un jour donné. On calcule $P(Y>10)= \approx 0,044$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
Arrondie au millième près, la probabilité qu'entre 5 et 10 ascenseurs tombent en panne un jour donné est 0,621.
Arrondie au millième près, la probabilité qu'entre 5 et 10 ascenseurs tombent en panne un jour donné est 0,621.2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Arrondie au millième près, la probabilité que plus de 10 ascenseurs tombent en panne un jour donné est 0,044.
Partie B
La fréquence des pannes est $f=\dfrac{263}{30\times 75}=\dfrac{263}{2250}\approx 0,117$.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
Exercice 4 6 points
Partie A
On donne ci-dessous la courbe représentative d'une fonction $f$ définie sur $\mathbb R$. La droite $(d)$ est tangente à cette courbe au point d'abscisse 0. 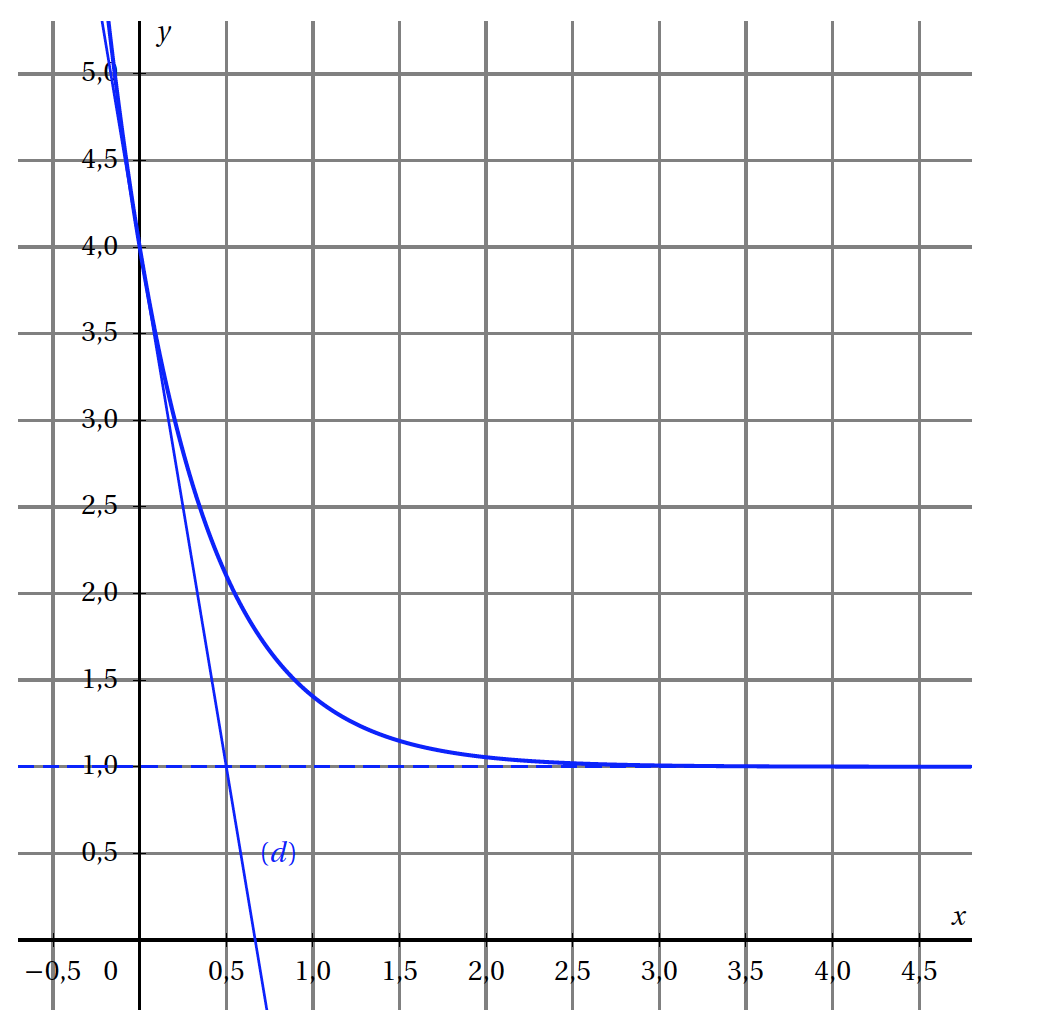
Donner par lecture graphique:
- La valeur de $f(0)$.
- La limite de $f$ en $+\infty$.
- Le tableau de variation de $f$.
- Le coefficient directeur de la tangente $(d)$ à la courbe représentative de $f$ au point d'abscisse 0.
Partie B
On considère l'équation différentielle $y'+2y=2$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et dérivable sur $\mathbb R$. On admet que la fonction représentée dans la Partie A est la solution de cette équation différentielle vérifiant $f(0)=4$.
- Démontrer que, pour tout réel $x$, on a $f(x)=3\text{e}^{-2x}+1$.
- Retrouver, en justifiant par des calculs, les résultats obtenus aux questions 2. 3. et 4. de la partie A.
Partie C
L'unité graphique est le dm (décimètre). On a représenté graphiquement ci-dessous la fonction $f$ sur l'intervalle $[0~;~4]$. On appelle $\mathcal{C}$ la courbe obtenue. 
On fait tourner la courbe $\mathcal{C}$ autour de l'axe des abscisses. On génère ainsi une surface dans l'espace ayant la forme d'un vase représenté ci-après en coupe et en perspective. 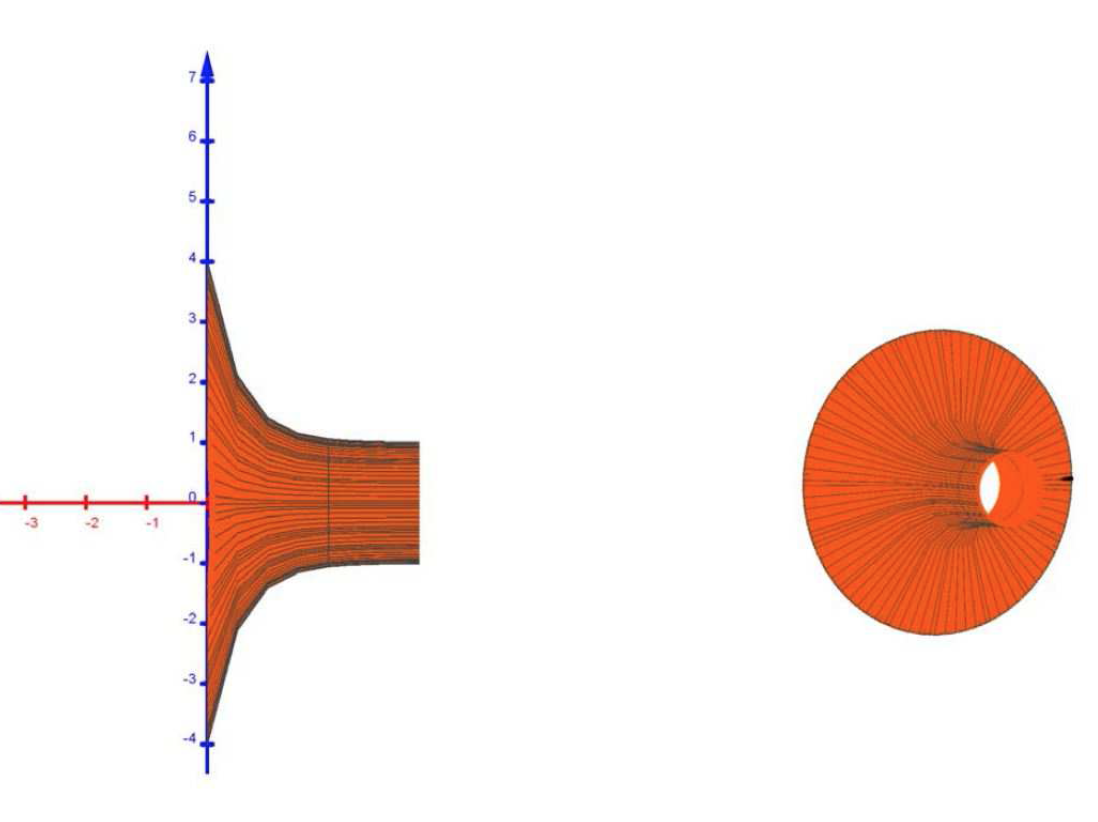
Le volume de ce vase, en dm$^3$, est donné par: \[V=\pi \times\displaystyle \int_{0}^{4} \left (f(x)\right )^2 \text{d} x.\]
- Montrer que, pour tout $x \in [0~;~4]$, on a $\left ( f(x)\right )^2 = 9\text{e}^{-4x} + 6\text{e}^{-2x}+1$.
- Calculer le volume du vase, exprimé en dm$^3$. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près.
- On désire remplir ce vase aux deux tiers du volume avec du sable coloré qui est vendu par sac de 3 dm$^3$. Déterminer le nombre minimum de sacs qu'il faut acheter.
Exercice 4 6 points
Partie A
On donne ci-dessous la courbe représentative d'une fonction $f$ définie sur $\mathbb R$. La droite $(d)$ est tangente à cette courbe au point d'abscisse 0. 
Donner par lecture graphique:
- La valeur de $f(0)$. $f(0)=4$
- La limite de $f$ en $+\infty$. La limite de $f$ en $+\infty$ est égale à 1.
- Le tableau de variation de $f$.
- Le coefficient directeur de la tangente $(d)$ à la courbe représentative de $f$ au point d'abscisse 0. Le coefficient directeur de la tangente $(d)$ à la courbe représentative de $f$ au point d'abscisse 0 est $-\dfrac{3}{0,5}=-6$.
Partie B
On considère l'équation différentielle $y'+2y=2$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et dérivable sur $\mathbb R$. On admet que la fonction représentée dans la Partie A est la solution de cette équation différentielle vérifiant $f(0)=4$.
- Démontrer que, pour tout réel $x$, on a $f(x)=3\text{e}^{-2x}+1$.
- L'équation différentielle $y'+2y=2$ est du type $y'=ay+b$ où $a=-2$ et $b=2$.
$y'+2y=2\iff y'=-2y+2$ - Une solution particulière de l'équation $y'+2y=2$ est la fonction $x \longmapsto=-\dfrac{b}{a}= 1$.
- On en déduit que les solutions de l'équation différentielle $y'+2y=2$ sont les fonctions $x \longmapsto k\text{e}^{-2x}+1$.
- La solution $f$ vérifiant $f(0)=4$ est telle que $k\text{e}^{0}+1=4$ ce qui entraîne $k=3$.
La solution de l'équation différentielle $y'+2y=2$ vérifiant $f(0)=4$ est donc la fonction $f$ définie par $f(x)=3\text{e}^{-2x} +1$.
- L'équation différentielle $y'+2y=2$ est du type $y'=ay+b$ où $a=-2$ et $b=2$.
- Retrouver, en justifiant par des calculs, les résultats obtenus aux questions 2. 3. et 4. de la partie A.
- On cherche $\displaystyle\lim_{x\to +\infty} f(x)$. $\left. \begin{array}{l} \displaystyle\lim_{x\to +\infty} -2x = -\infty\\ \text{On pose } X=-2x\\ \displaystyle\lim_{X\to -\infty} \text{e}^{X} = 0 \end{array} \right \rbrace$ donc $\displaystyle\lim_{x\to +\infty} \text{e}^{-2x} = 0$ et donc $\displaystyle\lim_{x\to +\infty} f(x)=1$
- Tableau de variations de $f$.
- On a vu que $\displaystyle\lim_{x\to +\infty} f(x)=1$.
- $\left. \begin{array}{l} \displaystyle\lim_{x\to -\infty} -2x = +\infty\\ \text{On pose } X=-2x\\ \displaystyle\lim_{X\to +\infty} \text{e}^{X} = +\infty \end{array} \right \rbrace$. donc $\displaystyle\lim_{x\to -\infty} \text{e}^{-2x} = +\infty$ et donc $\displaystyle\lim_{x\to -\infty} f(x)=+\infty$
- $f'(x)= 3\times (-2)\text{e}^{-2x} = -6\text{e}^{-2x}$ et $f'(x)<0$ sur $\mathbb R$; donc la fonction $f$ est strictement décroissante sur $\mathbb R$.
- On cherche le coefficient directeur de la tangente à la courbe en 0. Il est égal à $f'(0) = -6\text{e}^{0} = -6$.
Partie C
L'unité graphique est le dm (décimètre). On a représenté graphiquement ci-dessous la fonction $f$ sur l'intervalle $[0~;~4]$. On appelle $\mathcal{C}$ la courbe obtenue. 
On fait tourner la courbe $\mathcal{C}$ autour de l'axe des abscisses. On génère ainsi une surface dans l'espace ayant la forme d'un vase représenté ci-après en coupe et en perspective. 
Le volume de ce vase, en dm$^3$, est donné par: \[V=\pi \times\displaystyle \int_{0}^{4} \left (f(x)\right )^2 \text{d} x.\]
- Montrer que, pour tout $x \in [0~;~4]$, on a $\left ( f(x)\right )^2 = 9\text{e}^{-4x} + 6\text{e}^{-2x}+1$. $\left (f(x)\right )^2 = \left ( 3\text{e}^{-2x}+1 \right )^2 = 9\left (\text{e}^{-2x}\right )^2 +2\times 3\text{e}^{-2x}\times 1 + 1^2 = 9\text{e}^{-4x} +6\text{e}^{-2x}+1$
- Calculer le volume du vase, exprimé en dm$^3$. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près. Le volume du vase en dm$^3$ est $V=\pi \times \displaystyle\int_{0}^{4} \left (f(x)\right )^2 \text{d} x = \pi \times \displaystyle\int_{0}^{4} \left (9\text{e}^{-4x} +6\text{e}^{-2x}+1 \right ) \text{d} x$. Pour $a$ réel non nul, la fonction $x \longmapsto \text{e}^{ax}$ a pour primitive la fonction $x \longmapsto \dfrac{\text{e}^{ax}}{a}$ donc la fonction $x \longmapsto 9\text{e}^{-4x} +6\text{e}^{-2x}+1$ a pour primitive la fonction $x \longmapsto 9\dfrac{\text{e}^{-4x}}{-4} + 6 \dfrac{\text{e}^{-2x}}{-2} + x$ c'est-à-dire $x \longmapsto -\dfrac{9}{4}\text{e}^{-4x} -3\text{e}^{-2x} + x$. $\text{Donc }V= \pi \times \left [-\dfrac{9}{4}\text{e}^{-4x} -3\text{e}^{-2x} + x \right ]_{0}^{4} = \pi\times \left [ \left ( -\dfrac{9}{4}\text{e}^{-16} - 3\text{e}^{-8} + 4 \right ) - \left ( -\dfrac{9}{4}\text{e}^{0} - 3\text{e}^{0} +0\right ) \right ]\\ \phantom{\text{Donc }V} = \pi\times \left ( -\dfrac{9}{4}\text{e}^{-16} -3\text{e}^{-8} + \dfrac{37}{4}\right )$ dont une valeur approchée à $10^{-2}$ près est $29,06$. Le volume est donc d'environ $29,06$ dm$^3$.
- On désire remplir ce vase aux deux tiers du volume avec du sable coloré qui est vendu par sac de 3 dm$^3$. Déterminer le nombre minimum de sacs qu'il faut acheter. Il faudra donc $\dfrac{2}{3}\,V \approx 19,4$ dm$^3$ de sable; le sable est vendu par sac de 3 dm$^3$. Il faudra donc acheter 7 sacs de sable pour remplir le volume aux deux tiers.
- Vues: 22638
