Baccalauréat STL biotechnologies Polynésie 11 juin 2015
La calculatrice (conforme à la circulaire n° 99-186 du 16 novembre 1999) est autorisée. Le candidat est invité à faire figurer sur la copie toute trace de recherche, même incomplète ou non fructueuse, qu'il aura développée. Il sera tenu compte de la clarté des raisonnements et de la qualité de la rédaction dans l'appréciation des copies.
Exercice 1 3 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions, une seule des trois réponses proposées est exacte. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l’absence de réponse à une question ne rapportent ni n’enlèvent de point.
Indiquer, sans justification, le numéro de la question et la réponse correspondante sur la copie.
- On admet qu’une valeur mesurée suit une loi uniforme sur [0,995 ; 1,005]. La probabilité que la valeur mesurée soit comprise entre 0,998 et 1,002 est :
- 0,01
- 0,004
- 0,4
- 0,03
- Dans cette question, l’unité de mesure est le micromètre. Un élève mesure le diamètre de cellules de levure. Dans cette question, on admet que le résultat de la mesure $X$ suit une loi normale d’espérance 6 et d’écart type 2. La probabilité d’obtenir une mesure comprise entre 4 et 8 vaut à $10^{-3}$ près :
- 0,954
- 0,876
- 0,683
- 0,512
- Des élèves mesurent le diamètre de cellules de levure. Ils effectuent 50 mesures et observent que 15 d’entre elles donnent des diamètres supérieurs à $10\mu m$. Le nombre $p$ désigne la proportion de cellules dont le diamètre est supérieur à $10\mu m$ . L’intervalle de confiance de $p$, au niveau de confiance 95% avec des valeurs à $10^{-3}$ près, est :
- [0,282 ; 0,318]
- [0,173 ; 0,427]
- [9,7 ; 10,3]
Correction de l'exercice 1 (3 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions, une seule des trois réponses proposées est exacte. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l’absence de réponse à une question ne rapportent ni n’enlèvent de point.
Indiquer, sans justification, le numéro de la question et la réponse correspondante sur la copie.
- On admet qu’une valeur mesurée suit une loi uniforme sur [0,995 ; 1,005]. La probabilité que la valeur mesurée soit comprise entre 0,998 et 1,002 est :
- 0,01
- 0,004
- 0,4
- 0,03
La réponse est b.
- Dans cette question, l’unité de mesure est le micromètre. Un élève mesure le diamètre de cellules de levure. Dans cette question, on admet que le résultat de la mesure $X$ suit une loi normale d’espérance 6 et d’écart type 2. La probabilité d’obtenir une mesure comprise entre 4 et 8 vaut à $10^{-3}$ près :
- 0,954
- 0,876
- 0,683
- 0,512
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
La réponse est c.
- Des élèves mesurent le diamètre de cellules de levure. Ils effectuent 50 mesures et observent que 15 d’entre elles donnent des diamètres supérieurs à $10\mu m$. Le nombre $p$ désigne la proportion de cellules dont le diamètre est supérieur à $10\mu m$ . L’intervalle de confiance de $p$, au niveau de confiance 95% avec des valeurs à $10^{-3}$ près, est :
- [0,282 ; 0,318]
- [0,173 ; 0,427]
- [9,7 ; 10,3]
La fréquence est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times \8 $=\3 et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.
L' intervalle de confiance avec un niveau de confiance de 95% est : \[\9 = \left[\8 - 1,96\sqrt{\dfrac{\8(1 - \8)}{n}}~;~\8 + 1,96\sqrt{\dfrac{\8(1 - \8)}{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}} \right]\approx[\5~;~\6]\]
La réponse est b.
Exercice 2 6 points
On injecte dans le sang d’un malade un médicament à l’aide d’une perfusion. L’efficacité de ce médicament est optimale lorsque le débit de la perfusion est stable et que la concentration du produit ne dépasse pas 250 microgrammes (\micro g) par cm$^3$, seuil au-delà duquel des effets indésirables et toxiques apparaissent. On relève l’évolution de la concentration de ce médicament et on obtient les résultats suivants :
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{Temps }t_i \text{ en minutes } &0 & 2& 4 &6 & 10 &12 & 15\\\hline \text{ Concentration } c_i \text{ en } \mu g \text{ par }cm ^3 &0 &64&94 &130 & 195&220 & 230\\\hline \end{array} $$
Dans cet exercice, les résultats seront arrondis à $10^{-2}$.
Partie A
On pose : $y_i = \ln \left(250 - c_i\right)$ où $\ln$ désigne la fonction logarithme népérien.
- Recopier et compléter le tableau suivant (donner des valeurs arrondies à $10^{-2}$ ) :
$$ \begin{array}{|c|c|c|c|c|c|c|c|} \hline \text{ Temps } t_i \text{ en minutes } &0 & 2 & 4 & 6 & 10&12 & 15\\\hline y_i = \ln \left(250 - c_i\right) & & & & & & &\\\hline \end{array} $$ - Dans un repère orthogonal d’unités $1 cm $ en abscisse et $2 cm$ en ordonnée, représenter le nuage de points $M_i\ \left(t_i~;~ y_i\right)$ de la série statistique définie par le tableau précédent.
- Déterminer une équation de la droite $\mathcal{D}$ d’ajustement affine de $y$ en $t$ obtenue par la méthode des moindres carrés. Représenter cette droite dans le repère précédent.
- En déduire une relation entre la concentration $c$ et le temps $t$ sous la forme $c = A + B \text{e}^{k t}$.
Partie B
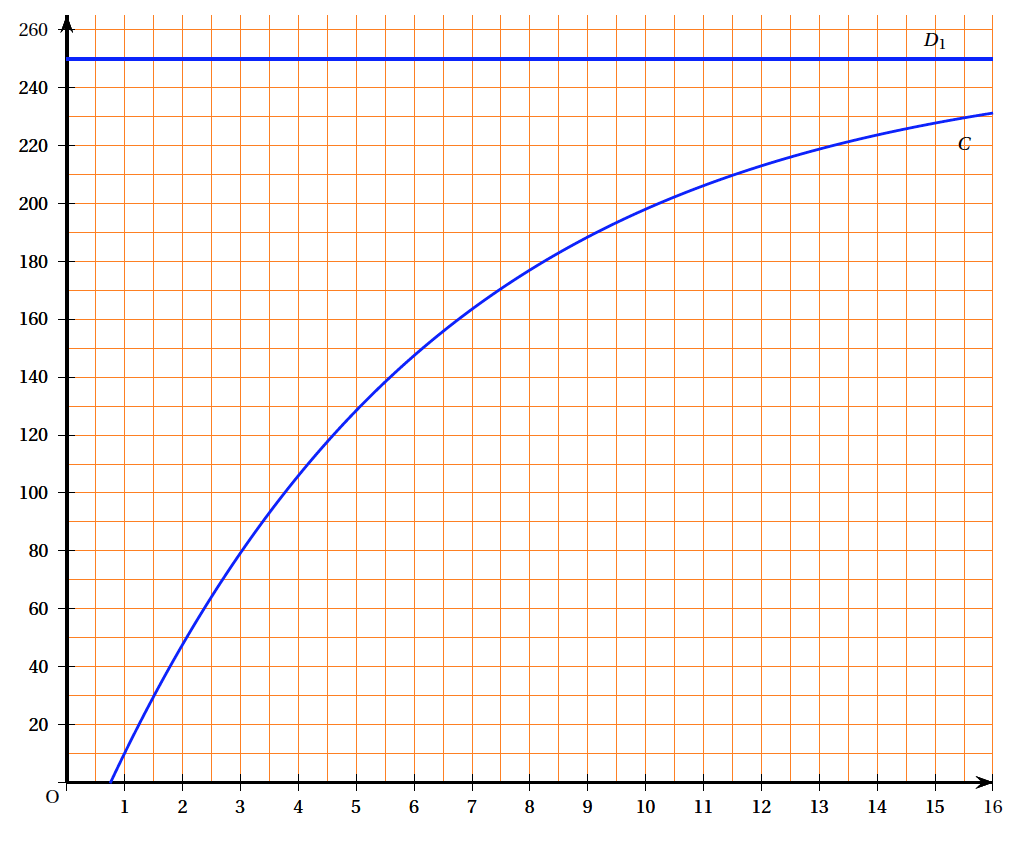
Soit la fonction $f$ définie sur $[0~;~+\infty[$ par $f(t)=250 - 284,29\text{e}^{- 0,17t}$. On admet que la fonction $f$ donne une bonne approximation de la concentration du médicament. La courbe $\mathcal{C}$ de la fonction $f$ et son asymptote $D_1$ d’équation $y = 250$ sont données en annexe 1.
- En justifiant, déterminer graphiquement le signe de la fonction dérivée de $f$ sur $[0~;~+\infty[$.
- En justifiant, déterminer graphiquement la limite de $f$ en $+\infty$.
- Justifier que la concentration du médicament ne dépasse pas $ 250\mu g$ par cm$^3$.
- Résoudre sur $[0,+\infty[$ l’inéquation $f (t) > 180$ .
- En déduire, à une minute près, le temps nécessaire pour atteindre la dose efficace qui est de $ 180\mu g$ par cm$^3$.
- Retrouver ce résultat en utilisant le graphique de la partie A (on expliquera la démarche utilisée en laissant les traits de construction apparents).
ANNEXE 1(À RENDRE AVEC LA COPIE)
EXERCICE 2
Correction de l'exercice 2 (5 points)
Exercice 3 7 points
Partie A
On considère l’équation différentielle (E) : $y' + 0,0865 y = 0 $ où $y$ est une fonction dérivable sur $[0~;~+\infty[$.
- Résoudre cette équation.
- Déterminer la fonction $f$ solution de (E) vérifiant la condition initiale : $f(0) = 4$.
Partie B
Le but de cette partie est l’étude de la décroissance radioactive de l’iode 131. On considère la fonction $N$ définie sur $[0~;~+\infty[$ par $N(t) = 4 \text{e}^{-0,0865 t}$. On admet que $N(t)$ donne le nombre de noyaux, exprimé en millions, d’iode 131 présents dans un échantillon à l’instant $t$ exprimé en jours. On note $C$ la courbe représentative de la fonction $N$.
- Déterminer la limite de $N(t)$ lorsque $t$ tend vers $+\infty$. En donner une interprétation physique.
- Soit $N '$ la fonction dérivée de $N$. Calculer $N '(t)$ .
- Étudier le signe de $N '$ , puis dresser le tableau de variation de la fonction $N$.
- Déterminer une équation de la tangente $T$ à $C$ au point d’abscisse 0.
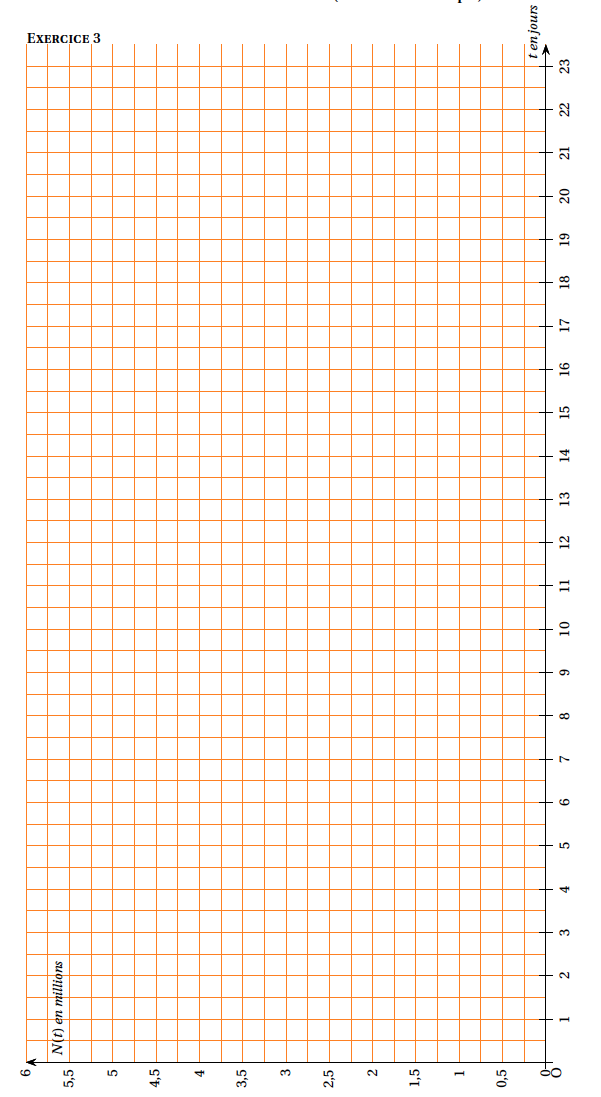
- Recopier et compléter le tableau suivant :
$$\begin{array} {|c|c|c|c|c|c|c|c||c|c|c|c|c|} \hline t \text{ en jours }&0 &2& 4 &6& 8& 10& 12& 14 &16& 18& 20& 25\\\hline N(t)&&&&&&&&&&&&\\\hline \end{array}$$
On donnera des valeurs approchées à 0,1 million. - Construire $T$ et $C$ dans le repère orthogonal donné en annexe 2.
- Calculer au bout de combien de jours le nombre de noyaux radioactifs est inférieur à 750000 .
- Retrouver ce résultat graphiquement (on laissera les traits de construction apparents).
- Déterminer graphiquement le temps nécessaire pour que le nombre de noyaux radioactifs passe de 4 millions à 2 millions, de 2 millions à 1 million, de 1 million à 500000 . Cette valeur est appelée durée de demi-vie de l’iode 131.
ANNEXE 2 (À RENDRE AVEC LA COPIE)
EXERCICE 3
Correction de l'exercice 3 (5 points)
Exercice 4 4 points
Partie A
Une population de bactéries a la propriété de doubler toutes les heures dans des conditions particulières. On suppose que cette capacité de doublement ne dépend pas du nombre initial de bactéries. Lors d’une expérience, Camille décide d’ajouter, chaque heure, un millier de bactéries du même type.
Elle écrit l’algorithme ci-contre : $$\begin{array}{|l|}\hline \text{ Saisir } N \\ H \text{ prend la valeur } 0\\ V \text{ prend la valeur } N\\ \text{ Tant que } V < 10^5 \\ \hspace{1.6em} H \text{ prend la valeur } H+1 \\ \hspace{1.6em} V \text{ prend la valeur } 2*V+ 1000 \\ \text{Fin Tant que }\\ \text{ Afficher } H \\\hline \end{array}$$
- Quelle est la valeur affichée par l’algorithme pour $N =10000$ ? On note $V_n$ le nombre de bactéries à la $nieme $ heure, $n$ étant un entier naturel. On admet que $V_0 = 10000 $.
- Exprimer $V_{n+1}$ en fonction de $V_n$ .
- La suite $( V_n )$ est-elle géométrique ? Justifier la réponse.
Partie B
Camille recommence l’expérience avec 10000 bactéries, dans des conditions différentes et sans ajouter de bactéries à chaque heure. Elle constate que :
- tant que le nombre de bactéries est strictement inférieur à 40000 , le nombre double toutes les heures ;
- à partir de 40000 bactéries, le nombre augmente seulement de 50% toutes les heures.
- Modifier l’algorithme précédent pour prendre en compte ces nouvelles conditions.
- Dans ces conditions, au bout de combien d’heures, le nombre de bactéries dépassera-t-il la valeur de $10^5$ ?
Exercice 4 4 points
- Vues: 17892
