Baccalauréat STI2D - STL Polynésie 16 juin 2014 spécialité SPCL - Exercice 4

Page 7 sur 8: Exercice 4

Exercice 4 7 points

Fonction logarithme

Soit $f$ la fonction définie sur $]0;+\infty[$ par : \[f(x) = 6 \ln x + ax + b\] où $a$ et $b$ sont des constantes réelles.
On appelle $\mathcal{C}_{f}$ la courbe représentative de la fonction $f$ dans un repère orthogonal $\left(\text{O},~\vec{i},\vec{j}\right)$.

• Le point A(1;1) appartient à $\mathcal{C}_{f}$.
• $\mathcal{C}_{f}$ admet une tangente horizontale en son point d'abscisse 2.

PARTIE A

Sur le graphique ci-dessous, on a tracé $\mathcal{C}_{f}$ (trait plein) ainsi que les courbes $\Gamma$ et $\Omega$. L'une de ces deux courbes est la représentation graphique de la fonction dérivée $f'$ de $f$ et l'autre représente une primitive $F$ de $f$.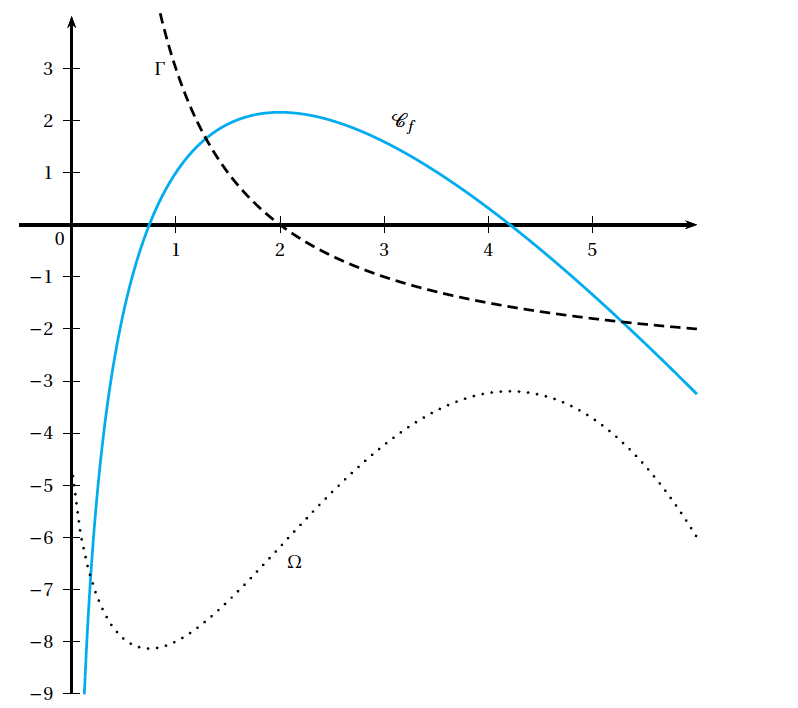

1. Indiquer laquelle des deux courbes est la représentation graphique de $F$.
2. Par lecture graphique, déterminer $f(1)$ et $f'(2)$.
3. Donner l'expression de $f'(x)$ en fonction de $x$ et de $a$.
4. l'aide des résultats précédents, montrer que pour tout $x$ de l'intervalle $]0; + \infty[$, \[f(x) = 6\ln x - 3x + 4.\]

PARTIE B

Dans cette partie, on pourra vérifier la cohérence des résultats obtenus avec la courbe $\mathcal{C}_{f}$ fournie dans la partie A.

1. Calculer la limite de la fonction $f$ lorsque $x$ tend vers $0$. Interpréter graphiquement cette limite.
2. Montrer que pour tout $x$ de l'intervalle $]0; + \infty[ , f'(x) = \dfrac{3}{x}(2 - x).$
3. Étudier le signe de $f'(x)$ puis donner les variations de la fonction $f$.
4. En déduire que la fonction $f$ admet un extremum dont on calculera la valeur exacte.

PARTIE C

Soit $H$ la fonction définie sur $]0; + \infty[$ par: \[H(x) = 6x\ln x - \dfrac{3}{2}x^2 - 2x.\]

1. Montrer que $H$ est une primitive de $f$ sur $]0; + \infty[$.
2. Calculer la valeur exacte de $I = \displaystyle\int_{1}^{\text{e}} f(x)\:\text{dx}.$
3. Donner une interprétation graphique du nombre $I$.
4. 1. l'aide du graphique, donner la valeur de $F(1)$.
   2. En déduire une expression de $F(x)$ pour tout $x$ dans l'intervalle $]0; + \infty[$.