Continuité
Exercice 01
Démontrer que l'équation $x^ 3 + 3 x = 5$ a une solution et une seule dans $\mathbb{R}$ .
Donner une valeur approchée à $10^ {-2}$ près de cette solution.
Exercice 02
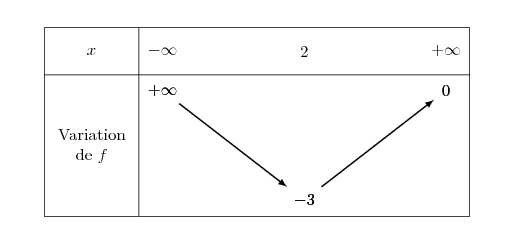
On donne ci-contre le tableau de variations de $f$.
Quel est le nombre de solutions de l'équation $f(x) = 1 $
(On justifiera le résultat)
Exercice 03
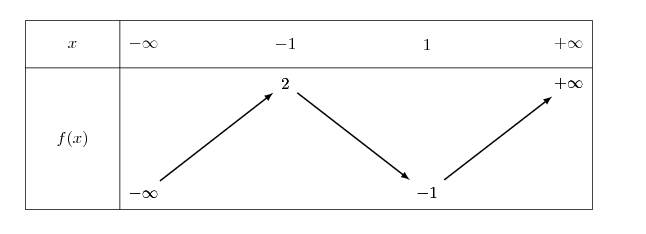
On donne ci-dessus le tableau de variations de $f$.
1°) Quel est le nombre de solutions de l'équation $f(x) = 0$
2°) Quel est le nombre de solutions de l'équation $f(x) = - 5$
(On justifiera les résultats)
Exercice 04
On considère l'équation $(E) : cos x = x$
1°) Montrer que si $x$ est solution de $(E)$ alors $0\leq x\leq\dfrac{\pi}{2} $ .
2°) Montrer que l'équation $(E)$ a une solution unique $\alpha$ dans $\mathbb{R}$ .
3°) Déterminer une valeur approchée de $\alpha$ à $10 ^{-2}$ près par défaut.
Exercice 05
Soit $ (C)$ la courbe représentative de la fonction $f$ définie sur $\mathbb{R}$ par $f(x) = 2 - x^ 2$
et $(C')$ la courbe représentative de la fonction $g$ définie sur $ [0 ; +\infty [$ par $ g(x) =\sqrt{3x}$ .
Quel est le nombre de points d'intersections de $(C)$ et de $(C')$ ? (Justifier)
Exercice 06
On considère la fonction $h$ définie sur $ [- 1 ; +\infty [$ par $ h(x) = 2 x - 3 +\sqrt{x+1}$ .
1°) Donner le tableau de variations de $h$ .
2°) En déduire que l'équation $h(x) = 0$ a une solution unique $\alpha$ dans $[- 1 ; +\infty [$ .
3°) Donner une valeur approchée de $\alpha$ à $ 10 ^{-2}$ près. (Facultatif : donner la valeur exacte de $\alpha$ )
- Vues: 24619
