Baccalauréat S Polynésie 13 juin 2014 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

1. Zoé se rend à son travail à pied ou en voiture. Là où elle habite, il pleut un jour sur quatre.Lorsqu'il pleut, Zoé se rend en voiture à son travail dans 80 % des cas.
Lorsqu'il ne pleut pas, elle se rend à pied à son travail avec une probabilité égale à $0,6$.
Affirmation n° 1 :
« Zoé utilise la voiture un jour sur deux. »

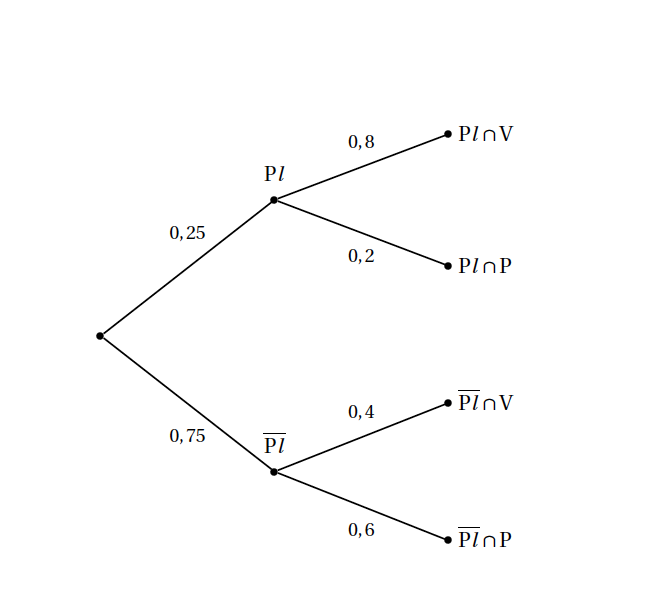
Pl: il pleut; V: en voiture; P: à pied
On cherche $p(V)$: $$\begin{array} p(V)&=p(V\cap \text{Pl})+p(V\cap \overline{\text{Pl}})\\ &=p_{\text{Pl}}(V)\times p(\text{Pl})+p_{\overline{\text{Pl}}}(V)\times p(\overline{\text{Pl}})\\ &= 0,8\times 0,25+0,4\times 0,75=0,5 \end{array}$$
«  Zoé utilise la voiture un jour sur deux. » 
Affirmation no 1 : VRAIE

2. Dans l'ensemble $E$ des issues d'une expérience aléatoire, on considère deux évènements $A$ et $B$.
   Affirmation n° 2 :« Si $A$ et $B$ sont indépendants, alors $A$ et $\overline{B}$ sont aussi indépendants. »

Dans l'ensemble $E$ des issues d'une expérience aléatoire, on considère deux événements $A$ et $B$.  $A$ et $B$ sont indépendants signifie que $p(A\cap B)=p(A)\times p(B)$: \[ p(A)=p(A\cap B)+p(A\cap\overline{B})=p(A)\times p(B)+p(A\cap\overline{B})\Longrightarrow p(A\cap\overline{B})=p(A)-p(A)\times p(B)=p(A)\left(1-p(B)\right)=p(A)\times p(\overline{B}) \]
«  Si $A$ et $B$ sont indépendants, alors $A$ et $\overline{B}$ sont aussi indépendants. » 
Affirmation no 2 : VRAIE

3. On modélise le temps d'attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $0,7$.
Affirmation n° 3 :
« La probabilité qu'un client attende au moins cinq minutes à ce guichet est $0,7$ environ. »
On modélise le temps d'attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $0,7$. Affirmation no 3 : FAUX $$ p(X<5)=\int_0^5 -0,7\text{e}^{-0,7x}\text{d}x=\left\lbrack-\text{e}^{-0,7x}\right\rbrack_0^5 =1-\text{e}^{-0,7\times 5}\approx 0,503 $$ «  La probabilité qu'un client attende au moins cinq minutes à ce guichet est $0,503$ environ. » Affirmation n° 4 :
« Le temps d'attente moyen à ce guichet est de sept minutes.»

Affirmation no 4 : FAUX $$ E(X)=\frac{1}{\lambda}=\frac{1}{0,7}\simeq 1,42 $$ « Le temps d'attente moyen à ce guichet est d'environ 1 minute et demi.» 
4. On sait que 39 % de la population française est du groupe sanguin A+. On cherche à savoir si cette proportion est la même parmi les donneurs de sang. On interroge $183$ donneurs de sang et parmi eux, 34 % sont du groupe sanguin A+.
   Affirmation n° 5 :
   « On ne peut pas rejeter, au seuil de 5 %, l'hypothèse selon laquelle la proportion de personnes du groupe sanguin A+ parmi les donneurs de sang est de 39 % comme dans l'ensemble de la population. »

On sait que 39 % de la population française est du groupe sanguin A+ ($p=0,39$). On cherche à savoir si cette proportion est la même parmi les donneurs de sang. On interroge $n=183$ donneurs de sang et parmi eux, 34 % sont du groupe sanguin A+  ($f=0,34$). On va trouver un intervalle de confiance au seuil de 95 %. $$\left\lbrack f-\frac{1}{\sqrt{n}}\,;\,f+\frac{1}{\sqrt{n}}\right\rbrack= \left\lbrack 0,34-\frac{1}{\sqrt{183}}\,;\,0,34+\frac{1}{\sqrt{183}}\right\rbrack\subset \left\lbrack 0,26~;~0,42\right\rbrack\ni p=0,39 $$ « On ne peut donc pas rejeter, au seuil de 5 %, l'hypothèse selon laquelle la proportion de personnes du groupe sanguin A+ parmi les donneurs de sang est de 39 % comme dans l'ensemble de la population. » 
Affirmation no 5 : VRAIE