Baccalauréat S Pondichéry 8 avril 2014 - Correction Exercice 3

Page 6 sur 11: Correction Exercice 3

Exercice 3 7 points

Commun à tous les candidats

1. Dans les trois situations ci-dessous, on a dessiné la courbe représentative $\mathcal{C}_{1}$ de la fonction $f$. Sur l'une d'entre elles, la courbe $\mathcal{C}_{2}$ de la fonction dérivée $f'$ est tracée convenablement. Laquelle ? Expliquer le choix effectué.
   
   
   
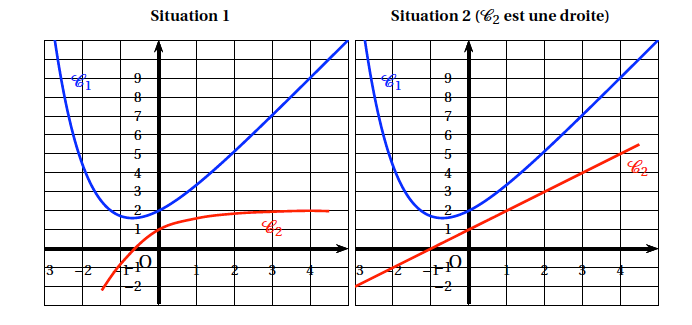
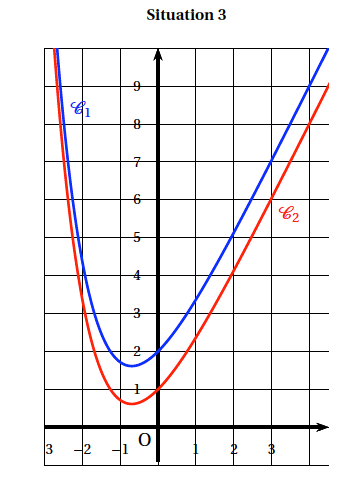La fonction $f$ est décroissante puis croissante, donc la fonction dérivée doit être négative puis positive, ce qui élimine la situation 3.

 

Si la fonction dérivée est représentée par une droite comme dans la situation 2, c'est que la fonction $f$ est une fonction du second degré; donc sa représentation graphique possède un axe de symétrie vertical. Ce n'est pas le cas donc on peut éliminer la situation 2. La bonne situation est donc la situation 1.
1. Déterminer l'équation réduite de la droite $\Delta$ tangente à la courbe $\mathcal{C}_{1}$ en A.
La droite $\Delta$ tangente à la courbe $\mathcal C_1$ en A d'abscisse 0, a pour équation $y= f'(0)(x-0)+f(0)$. $f(0)$ est l'ordonnée de A donc $f(0)=2$; $f'(0)$ est l'ordonnée du point B donc $f'(0)=1$. L'équation réduite de la tangente est donc: $y=x+2$.
2. On sait que pour tout réel $x,\: f(x) = \text{e}^{-x} + ax + b$ où $a$ et $b$ sont deux nombres réels.
   1. Déterminer la valeur de $b$ en utilisant les renseignements donnés par l'énoncé.
   $f(0)=2 \iff\,\text{e}\,^{0} + 2\times 0 + b = 2 \iff 1+b=2 \iff b=1$
   2. Prouver que $a = 2$.
    $b=1$ donc $f(x)=\,\text{e}\,^{-x}+ax+1$ donc 
   
   
   $f'(x)= -\,\text{e}\,^{-x}+a$; or $f'(0)=1 \iff -\,\text{e}\,^{0}+a = 1 \iff 1+a=1 \iff a=2$
   
   
   Donc $f(x)=\,\text{e}\,^{-x}+2x+1$
3. Étudier les variations de la fonction $f$ sur $\mathbb{R}$.
On a vu que $f'(x)=-\,\text{e}\,^{-x}+a$ et comme $a=2$, $f'(x)=-\,\text{e}\,^{-x}+2$. $f'(x) >0 \iff -\,\text{e}\,^{-x}+2>0 \iff 2 >\,\text{e}\,^{-x} \iff \ln 2 > -x \iff -\ln 2 < x$

 

$$\begin{array}{ l l} \text{Donc:} & \text{la fonction } f \text{ est strictement décroissante sur } \\texttt{]} -\infty\:; -\ln 2 \\texttt{]}; \\ & \text{ la fonction } f \text{ admet un minimum pour } x=-\ln 2;\\ & \text{la fonction } f \text{ est strictement croissante sur } \\texttt{[} -\ln 2\:; +\infty \\texttt{[}. \end{array}$$
1. Déterminer la limite de la fonction $f$ en $+ \infty$.
On sait que $\displaystyle\lim_{x \to +\infty}\,\text{e}\,^{-x}=0$ et que $\displaystyle\lim_{x \to +\infty} 2x+1=+\infty$ donc, par somme, $\displaystyle\lim_{x \to +\infty} f(x)=+\infty$.

1. 1. Montrer que la fonction $g$ admet $0$ comme minimum sur $\mathbb{R}$.
   $g'(x)=f'(x)-1 = -\,\text{e}\,^{-x}+2-1 = -\,\text{e}\,^{-x}+1$. $g'(x)>0 \iff -\,\text{e}\,^{-x}+1 >0 \iff 1 >\,\text{e}\,^{-x} \iff \ln 1 > -x \iff x>0$ Donc $g$ est strictement décroissante sur $\mathbb{R}_{-}$, et strictement croissante sur $\mathbb{R}_{+}$; la fonction $g$ admet donc un minimum en $x=0$. Ce minimum vaut $g(0)=f(0)-(0+2) = 2-2 = 0$.
   2. En déduire la position de la courbe $\mathcal{C}_{1}$ par rapport à la droite $\Delta$.
   D'après la question précédente, pour tout réel $x$: $g(x) \geq 0$ donc $f(x)-(x+2)\geq 0 \iff f(x) \geq x+2$ ce qui veut dire que la courbe $\mathcal C_1$ est au-dessus de la droite $\Delta$ sur $\mathbb{R}$.

La figure 2 ci-dessous représente le logo d'une entreprise. Pour dessiner ce logo, son créateur s'est servi de la courbe $\mathcal{C}_{1}$ et de la droite $\Delta$, comme l'indique la figure 3 ci-dessous. Afin d'estimer les coûts de peinture, il souhaite déterminer l'aire de la partie colorée en gris.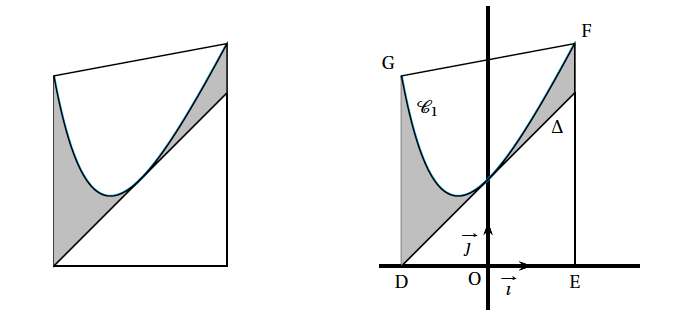

Le contour du logo est représenté par le trapèze DEFG où :

• D est le point de coordonnées $(-2 ; 0)$,
• E est le point de coordonnées (2 ; 0),
• F est le point d'abscisse 2 de la courbe $\mathcal{C}_{1}$,
• G est le point d'abscisse $- 2$ de la courbe $\mathcal{C}_{2}$.

La partie du logo colorée en gris correspond à la surface située entre la droite $\Delta$, la courbe $\mathcal{C}_{1}$, la droite d'équation $x = - 2$ et la droite d'équation $x = 2$.

1. Calculer, en unités d'aire, l'aire de la partie du logo colorée en gris (on donnera la valeur exacte puis la valeur arrondie à $10^{-2}$ du résultat).
On a vu que la courbe $\mathcal C_1$ était au dessus de la droite $\Delta$ sur $\mathbb{R}$ donc c'est vrai sur $ \\texttt{[} -2\:; 2 \\texttt{]}$.

 

De plus, la courbe $\mathcal C_1$ et la droite $\Delta$ sont toutes les deux au-dessus de l'axe des abscisses sur l'intervalle $ \\texttt{[} -2\:; 2 \\texttt{]}$.

 

L'aire de la partie grisée est égale à la différence de l'aire sous la courbe $\mathcal C_1$ entre $x=-2$ et $x=2$, et l'aire sous la droite entre $x=-2$ et $x=2$.

 

Autrement dit cette aire est égale à $\displaystyle\int_{-2}^2 f(x) \,\text{d}x - \displaystyle\int_{-2}^2 (x+2) \,\text{d} x = \displaystyle\int_{-2}^2 f(x)-(x+2) \,\text{d} x = \displaystyle\int_{-2}^2 g(x) \,\text{d} x $ $g(x)=\,\text{e}\,^{-x}+2x+1-x-2 =\,\text{e}\,^{-x} +x -1$;

 

donc $g$ a pour primitive la fonction $G$ telle que $G(x)=-\,\text{e}\,^{-x} + \dfrac{x^2}{2}-x$.

 

$\displaystyle\int_{-2}^2 g(x) \,\text{d} x = G(2)-G(-2)=\left[ -\,\text{e}\,^{-x} + \dfrac{x^2}{2}-x \right]_{-2}^2 = \left (-\,\text{e}\,^{-2} + \dfrac{2^2}{2}-2 \right ) - \left ( -\,\text{e}\,^{-(-2)} +\dfrac{(-2)^2}{2} -(-2)\right )$

 

$ \displaystyle\int_{-2}^2 g(x) \,\text{d} x = -\,\text{e}\,^{-2} + 2 - 2 +\,\text{e}\,^2 - 2 - 2 =\,\text{e}\,^2 -\,\text{e}\,^{-2} - 4$

 

$  \displaystyle\int_{-2}^2 g(x) \,\text{d}x \approx 3,25$ unités d'aire.