Baccalauréat S Asie 22 juin 2017 - Correction Exercice 4

Page 8 sur 12: Correction Exercice 4

Exercice 4 3 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

L'objet du problème est l'étude des intégrales $I$ et $J$ définies par : $$I = \displaystyle\int_0^1 \dfrac{1}{1 + x}\:\text{d}x\quad \text{ et }\quad J = \displaystyle\int_0^1 \dfrac{1}{1 + x^2}\:\text{d}x.$$

Partie A : valeur exacte de l'intégrale $I$

 

1. Donner une interprétation géométrique de l'intégrale $I$.
$I$ est l’aire du domaine compris entre la courbe représentant la fonction $x\mapsto \dfrac{1}{1+x}$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$.
$\quad$
2. Calculer la valeur exacte de $I$.
$\begin{align*} \displaystyle I&=\int_0^1\dfrac{1}{1+x} \;dx \\ &=\big[\ln(1+x)\big]_0^1 \\ &=\ln(2)-\ln(1) \\ &=\ln(2) \end{align*}$

 

Partie B : estimation de la valeur de $J$

Soit $g$ la fonction définie sur l'intervalle $[0~;~1]$ par $g(x) = \dfrac{1}{1 + x^2}$. On note $\mathcal{C}_g$ sa courbe représentative dans un repère orthonormé du plan. On a donc : $J = \displaystyle\int_0^1 g(x)\:\text{d}x$. Le but de cette partie est d'évaluer l'intégrale $J$ à l'aide de la méthode probabiliste décrite ci-après. On choisit au hasard un point M$\,(x~;~y)$ en tirant de façon indépendante ses coordonnées $x$ et $y$ au hasard selon la loi uniforme sur [0~;~1]. On admet que la probabilité $p$ qu'un point tiré de cette manière soit situé sous la courbe $\mathcal{C}_g$ est égale à l'intégrale $J$. En pratique, on initialise un compteur $c$ à $0$, on fixe un entier naturel $n$ et on répète $n$ fois le processus suivant :

• on choisit au hasard et indépendamment deux nombres $x$ et $y$, selon la loi uniforme sur $[0~;~1]$ ;
• si M$\,(x~;~y)$ est au-dessous de la courbe $\mathcal{C}_g$ on incrémente le compteur $c$ de 1.

On admet que $f = \dfrac{c}{n}$ est une valeur approchée de $J$. C'est le principe de la méthode dite de Monte-Carlo. La figure ci-dessous illustre la méthode présentée pour $n = 100$. $100$ points ont été placés aléatoirement dans le carré. Les disques noirs correspondent aux points sous la courbe, les disques blancs aux points au-dessus de la courbe. Le rapport du nombre de disques noirs par le nombre total de disques donne une estimation de l'aire sous la courbe.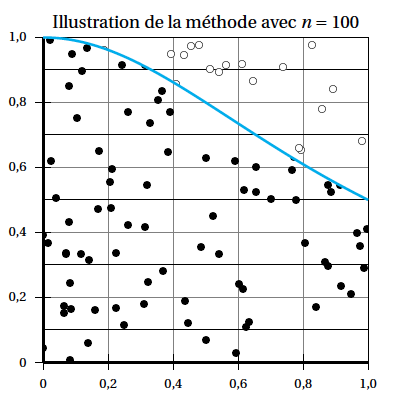

1. Recopier et compléter l'algorithme ci-après pour qu'il affiche une valeur approchée de $J$. $$\begin{array}{ |c|c| }\hline \text{Variables}& n , c, f, i, x, y \text{ sont des nombres}\\ \hline &\text{ Lire la valeur de } n\\ &c \text{ prend la valeur }\ldots \\ &\text{ Pour i allant de 1 à }\ldots{} \text{ faire }\\ &\hspace{0.5cm}x \text{ prend une valeur aléatoire entre 0 et 1}\\ \text{Traitement} &\hspace{0.5cm}y \text{ prend }\ldots {}\\ &\hspace{0.5cm}\text{ Si }{}\ldots {} \text{ alors }\\ &\hspace{0.5cm}\ldots \text{ prend la valeur } \ldots{}\\ &\hspace{0.5cm} \text{ Fin si }\\ &\text{ Fin pour}\\ &f\text{ prend la valeur }{}\ldots{}\\ \hline \text{Sortie}&\text{ Afficher }f\\ \hline \end{array}$$
Variables
$\quad$ $n,c,f,i,x,y$ sont des nombres
Traitement
$\quad$ Lire la valeur de $n$
$\quad$ $c$ prend la valeur $0$
$\quad$ pour $i$ allant de $1$ à $n$ faire
$\qquad$ $x$ prend une valeur aléatoire entre $0$ et $1$
$\qquad$ $y$ prend la valeur une valeur aléatoire entre $0$ et $1$
$\qquad$ Si $y< \dfrac{1}{1+x^2}$ alors
$\qquad$ $\quad$ $c$ prend la valeur $c+1$
$\qquad$ Fin si
$\quad$ Fin pour
$\quad$ $f$ prend la valeur $\dfrac{c}{n}$
Sortie
$\quad$ Afficher $f$
$\quad$
2. Pour $n = 1000$, l'algorithme ci-dessus a donné pour résultat : $f = 0,781$. Donner un intervalle de confiance, au niveau de confiance de 95 %, de la valeur exacte de $J$.
On a $n=1~000 \geq 30$ et $f=0,781$ donc $nf=781 \geq 5$ et $n(1-f)=219\geq 5$.
Un intervalle de confiance au niveau de confiance de $95\%$, est donc :
$\begin{align*} I_{1~000}&=\left[0,781-\dfrac{1}{\sqrt{1~000}};0,781+\dfrac{1}{\sqrt{1~000}}\right] \\&\approx [0,749;0,813] \end{align*}$

3. Quelle doit-être, au minimum, la valeur de $n$ pour que l'intervalle de confiance, au niveau de confiance de 95 %, ait une amplitude inférieure ou égale à $0,02$ ?
Un intervalle de confiance est de la forme $\left[f-\dfrac{1}{\sqrt{n}};f+\dfrac{1}{\sqrt{n}}\right]$.
Donc son amplitude est $f+\dfrac{1}{\sqrt{n}}-\left(f-\dfrac{1}{\sqrt{n}}\right)=\dfrac{2}{\sqrt{n}}$.
On veut donc résoudre :
$\dfrac{2}{\sqrt{n}}=0,02 \iff \sqrt{n}=100 \iff n=10~000$
$\quad$ La valeur minimale de $n$ est 10000.