Bac STI2D Polynésie 9 juin 2016 - Exercice 4

Page 7 sur 8: Exercice 4

Exercice 4 6 points

Fonctions

 

Partie A : Lecture graphique

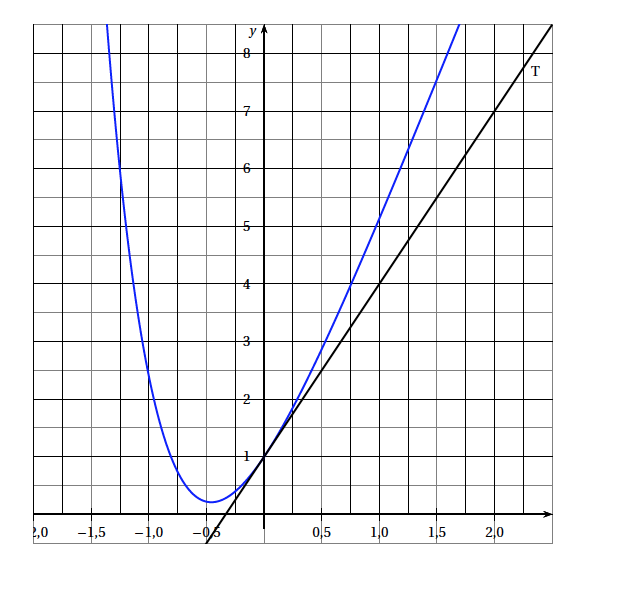
On considère la courbe $C$ associée à une fonction $f$ représentée en ANNEXE 2 avec la droite T, tangente à la courbe $C$ au point d'abscisse $0$.

1. Résoudre graphiquement sur l'intervalle $[- 1~;~1,5]$ et avec la précision permise par le dessin les deux inéquations suivantes:
   1. $f(x) \geqslant 1$
   2. $f'(x) \geqslant 0$.
2. 1. Donner l'équation. de la tangente T à la courbe $C$ au point de coordonnées (0 ; 1) en sachant que cette tangente passe par le point de coordonnées (2 ; 7).
   2. En déduire le nombre dérivé $f'(0)$.

 

Partie B : Étude de la fonction $f$

Soit $f$ la fonction définie sur $\mathbb R$ par la relation $f(x) = \text{e}^{-2x} + 5x$.

1. Déterminer, en la justifiant, la limite de $f$ en $+ \infty$. On admet pour la suite que la limite de $f$ en $- \infty$ est $+ \infty$.
2. Calculer $f'(x)$ et étudier son signe sur $\mathbb R$.
3. En déduire le tableau des variations de la fonction $f$ sur $\mathbb R$.
4. 1. Déterminer à partir du tableau des variations le nombre de solutions de l'équation $f(x) = 2$.
   2. Donner une valeur arrondie à $10^{-2}$ près de chaque solution.

 

Partie C. : Calcul d'aire

On admet :

• que la courbe $C$ de la partie A est la représentation de la fonction $f$ définie dans la partie B ;
• que la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$.

L'objectif de cette partie est de déterminer par un calcul l'aire $\mathcal{A}$ comprise entre la courbe $C$, la droite T et les droites verticales d'équations $x = 0$ et $x = 1,5$.

1. Hachurer sur le dessin, en ANNEXE 2, l'aire $\mathcal{A}$ que l'on veut déterminer.
2. 1. Déterminer une primitive de la fonction $g$ définie sur $\mathbb R$ par : \[\text{pour tout réel }\:x,\: g(x) = \text{e}^{-2x} + 2x - 1.\]
   2. Justifier que l'aire $\mathcal{A}$ recherchée vaut, en unité d'aire: \[\mathcal{A} = \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\]
   3. En déduire la valeur exacte puis l'arrondi à $10^{- 2}$ de $\mathcal{A}$.
      
      

 

Exercice 4 Parties A et C