Bac STI2D Polynésie 9 juin 2016
Exercice 1 3 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte $1$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point. Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.
Dans cet exercice, $\text{i}$ désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$.
- L'écriture exponentielle du nombre complexe $z = \dfrac{-3\text{i}}{1 + \text{i}}$ est :
\[ \textbf{a.} z = \frac{3\sqrt{2}}{2}\text{e}^{-\text{i}\frac{5\pi}{4}}\hspace{2cm}\textbf{b.}z = - \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}}\hspace{2cm} \textbf{c.} z =\frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}} \hspace{2cm} \textbf{d.} z = \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{\pi}{4}} \] - Soit $f$ la fonction définie pour tout réel $t$ positif par : $f(t) = 8\text{e}^{-0,12t }+11$. La valeur moyenne de $f$ arrondie à $10^{-1}$ sur l'intervalle [0;24] est :
$$ \textbf{a. }15,2\hspace{2cm} \textbf{b. }13,6 \hspace{2cm} \textbf{c }16,7 \hspace{2cm}\textbf{d. } 11,2$$ - On donne dans un repère orthonormé les points : A(0;2) ; B(1;3) ; C$(-2;1)$ et D$(-1;0)$. Le produit scalaire $\vec{\text{AB}} \cdot \vec{\text{CD}}$ est égal à :
$$ \textbf{a.} \vec{\text{AB}} \cdot \vec{\text{CD}} = 0 \hspace{2cm}\hspace{2cm}\hspace{2cm} \textbf{b.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{0} \hspace{2cm}\hspace{2cm} \textbf{c.} \vec{\text{AB}} \cdot \vec{\text{CD}} = - 2 \hspace{2cm} \textbf{d.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{\text{AD}}$$
Exercice 1 3 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte $1$ point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point. Pour répondre, vous recopierez sur votre copie le numéro de la question et la seule réponse choisie.
Dans cet exercice, $\text{i}$ désigne le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$.
- L'écriture exponentielle du nombre complexe $z = \dfrac{-3\text{i}}{1 + \text{i}}$ est :
\[ \textbf{a.} z = \frac{3\sqrt{2}}{2}\text{e}^{-\text{i}\frac{5\pi}{4}}\hspace{2cm}\textbf{b.}z = - \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}}\hspace{2cm} \textbf{c.} z =\frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{5\pi}{4}} \hspace{2cm} \textbf{d.} z = \frac{3\sqrt{2}}{2}\text{e}^{\text{i}\frac{\pi}{4}} \] Bonne réponse : c
- Module : \begin{align*} |z| &= \sqrt{\left (\dfrac{3}{2}\right )^2+\left (\dfrac{3}{2}\right )^2}\\ &= \sqrt{ \dfrac{9}{4} +\dfrac{9}{4}}\\ &=\sqrt{ \dfrac{18}{4} } \\ &= \dfrac{3\sqrt{2}}{2} \end{align*}
- Argument :
$$\left\lbrace \begin{array}{l} \cos \theta=\dfrac{a}{r}=\dfrac{-\dfrac{3}{2}}{\dfrac{3\sqrt{2}}{2}}= -\dfrac{3}{2}\times \dfrac{2}{3\sqrt 2}=-\dfrac{\sqrt 2}{2}\\ \sin \theta=\dfrac{b}{r}=\dfrac{-\dfrac{3}{2}}{\dfrac{3\sqrt{2}}{2}}= -\dfrac{3}{2}\times \dfrac{2}{3\sqrt 2}=-\dfrac{\sqrt 2}{2} \end{array} \right.$$ Donc $\theta = -\dfrac{3\pi}{4}$ convient ou en ajoutant $2\pi$,$\theta = -\dfrac{3\pi}{4}+2\pi= \dfrac{5\pi}{4}$ - On utilise la calculatrice :( en mode degré) pour les vieilles TI83 ...
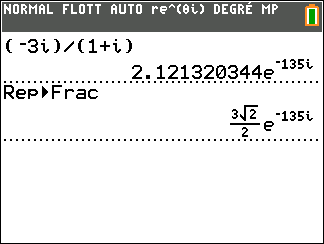
- On utilise la calculatrice :( en mode radian) pour la TI83 Premium ...
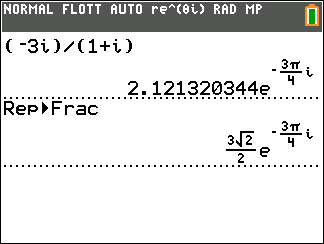
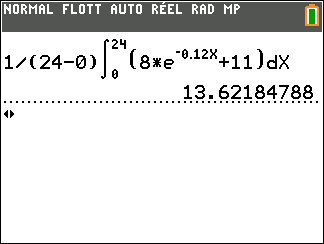
- Soit $f$ la fonction définie pour tout réel $t$ positif par : $f(t) = 8\text{e}^{-0,12t }+11$. La valeur moyenne de $f$ arrondie à $10^{-1}$ sur l'intervalle [0;24] est :
$$ \textbf{a. }15,2\hspace{2cm} \textbf{b. }13,6 \hspace{2cm} \textbf{c }16,7 \hspace{2cm}\textbf{d. } 11,2$$ Bonne réponse : b
- On met tout d'abord $z$ sous forme algégrique $z = \dfrac{-3\text{i}}{1 + \text{i}}$ sous forme algébrique : \begin{align*} z &= \dfrac{-3\text{i}}{1 + \text{i}}\\ &= \dfrac{-3\text{i}(1 - \text{i})}{(1 + \text{i})(1 - \text{i})}\\ &=\dfrac{-3\text{i} +3\text{i}^2 }{(1^2 + 1^2)} \\ &=\dfrac{-3-3\text{i} }{2} \end{align*} $z=a+\text{i}b$ où $a= -\dfrac{3}{2}$ et $b= -\dfrac{3}{2}$
- Une méthode rapide ? On utilise la calculatrice :
|
|
- Le calcul direct : la valeur moyenne d'une fonction $f$ sur $[ a; b]$ est $V_{Moy}= \dfrac{1}{b-a}\displaystyle\int_a^b \; f(t)\; dt$
- On donne dans un repère orthonormé les points : A(0;2) ; B(1;3) ; C$(-2;1)$ et D$(-1;0)$. Le produit scalaire $\vec{\text{AB}} \cdot \vec{\text{CD}}$ est égal à :
$$ \textbf{a.} \vec{\text{AB}} \cdot \vec{\text{CD}} = 0 \hspace{2cm}\hspace{2cm}\hspace{2cm} \textbf{b.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{0} \hspace{2cm}\hspace{2cm} \textbf{c.} \vec{\text{AB}} \cdot \vec{\text{CD}} = - 2 \hspace{2cm} \textbf{d.} \vec{\text{AB}} \cdot \vec{\text{CD}} = \vec{\text{AD}}$$ Bonne réponse : a
- Ici $f(t)= 8\text{e}^{-0,12t }+11$, une primitive est donc la fonction $F$ dénie sur $\mathbb R$ par $F(t) = \dfrac{8}{-0,12}\text{e}^{-0,12t }+11t$ \begin{align*} V_{Moy} &= \dfrac{1}{24}\displaystyle\int_0^{24} \; f(t)\; dt \\ &= \dfrac{1}{24}\left (F(24)-F(0)\right )\\ F(24)&= \dfrac{8}{-0,12}\text{e}^{-0,12\times 24 }+11\times 24\approx 260,26 \\ F(0)&= \dfrac{8}{-0,12}\text{e}^{ 0}+11\times 0\approx -66.6 7 \\ V_{Moy} &\approx \dfrac{1}{24} (326.92)\approx 13,6 \end{align*}
- On a $\vec{AB} \begin{pmatrix} x_B-x_A \\y_B-y_A \end{pmatrix}= \begin{pmatrix} 1-0 \\3-2 \end{pmatrix}= \begin{pmatrix} 1 \\1 \end{pmatrix}$ de même on obtient $\vec{CD} \begin{pmatrix} 1 \\-1 \end{pmatrix}$ \begin{align*} \vec{\text{AB}} \cdot \vec{\text{CD}} &= XX'+YY'\\ &= 1\times 1 + (-1)\times 1\\ &= 1-1 \\ &=0 \end{align*}
Exercice 2 6 points
L'énergie photovoltaïque voit son coût baisser de façon importante depuis plusieurs années, ce qui engendre une croissance forte de ce secteur. L'évolution de la puissance solaire photovoltaïque installée dans le monde entre fin 2004 et fin 2015 est résumée dans le graphique ci-dessous : 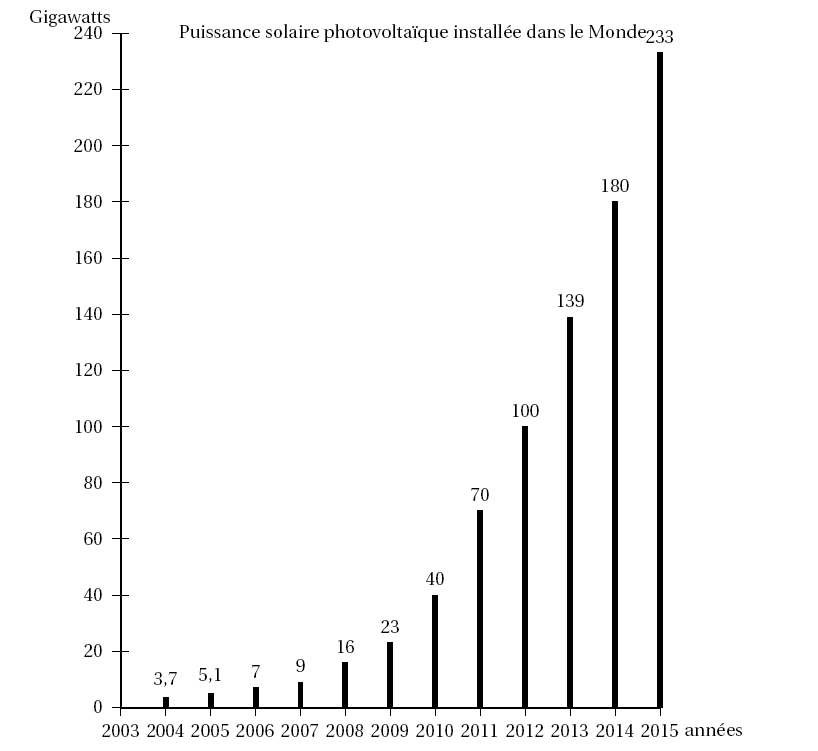
- Calculer les pourcentages d'augmentation annuels entre 2013 et 2014 ainsi qu'entre 2014 et 2015 $\left(\text{arrondir à } 10^{-1}\right)$. On se propose d'estimer la puissance solaire photovoltaïque installée dans le monde dans les 15 ans à venir, si le taux de croissance annuel reste constant et égal à 30%. On note $P_n$ la puissance solaire photovoltaïque installée dans le monde, en GW, à la fin de l'année $2015 + n$. On a ainsi $P_0 = 233$.
- Calculer $P_1$ puis $P_2$ $\left(\text{arrondir à } 10^{-1}\right)$.
- Exprimer $P_{n+1}$ en fonction de $P_n$.
- En déduire la nature de la suite $\left(P_n\right)$ et donner ses éléments caractéristiques.
- Exprimer $P_n$ en fonction de $n$.
- Calculer la puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 (arrondir à l'unité).
- Quel est le pourcentage global d'augmentation de cette puissance solaire mondiale entre 2015 et 2025 (arrondir à l'unité) ?
- On veut déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde atteindrait 16000 GW. Pour atteindre cette puissance, les panneaux photovoltaïques occuperaient au sol l'équivalent d'un carré de 400km de côté et suffiraient pour produire toute l'électricité consommée dans le monde (consommation domestique, industrielle et des transports).
- On considère l'algorithme ci-dessous. Recopier et compléter les lignes 3 et 7 afin que cet algorithme réponde à la question posée. $$ \begin{array}{|l |l|}\hline 1/& \text{ Affecter à } N \text{ la valeur } 0 \\ 2/& \text{ Affecter à } P \text{ la valeur } 233\\ 3/& \text{ Tant que } \ldots\\ 4/&\text{ Affecter à } N \text{ la valeur } N +1 \\ 5/&\text{ Affecter à } P \text{ la valeur } P \times 1,30 \\ 6/&\text{ Fin Tant que }\\ 7/& \text{ Afficher } \ldots\\ \hline \end{array} $$
- En faisant tourner cet algorithme complété, déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde dépasserait 16000 GW.
- Proposer une autre méthode, directe et non algorithmique, pour répondre à la question précédente en détaillant la démarche utilisée.
Exercice 2 6 points
L'énergie photovoltaïque voit son coût baisser de façon importante depuis plusieurs années, ce qui engendre une croissance forte de ce secteur. L'évolution de la puissance solaire photovoltaïque installée dans le monde entre fin 2004 et fin 2015 est résumée dans le graphique ci-dessous : 
- Calculer les pourcentages d'augmentation annuels entre 2013 et 2014 ainsi qu'entre 2014 et 2015 $\left(\text{arrondir à } 10^{-1}\right)$. $\dfrac{180}{139} \approx 1,295 $ et $\dfrac{233}{180}\approx 1,294$.
- Calculer $P_1$ puis $P_2$ $\left(\text{arrondir à } 10^{-1}\right)$. On calcule $P_1= P_0 + 30\%\times P_0 = 233\times \left(1+\dfrac{30}{100}\right)= 1,3 \times 233 = 302,9$
- Exprimer $P_{n+1}$ en fonction de $P_n$. $\begin{align*} P_{n+1}&= P_n + 30\%\times P_n\\ & = \left(1+\dfrac{30}{100}\right)\times P_n\\ &= 1,3P_n \end{align*}$
- En déduire la nature de la suite $\left(P_n\right)$ et donner ses éléments caractéristiques. Ayant pour tout entier naturel $n$ ; $P_{n+1}=1,3P_n$, on déduit que la suite $\left(P_n\right)$ est géométrique de raison 1,3.
- Exprimer $P_n$ en fonction de $n$. Comme la suite $\left(P_n\right)$ est géométrique, on a $P_n=q^n \times P_0$ $$P_n=1,3^n \times 233$$
- Calculer la puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 (arrondir à l'unité). La puissance solaire photovoltaïque, en GW, installée dans le monde fin 2025 est donnée par $P_{10}=1,3^{10}\times 233\approx 3212$
- Quel est le pourcentage global d'augmentation de cette puissance solaire mondiale entre 2015 et 2025 (arrondir à l'unité) ? On calcule $t$ tel que $P_{10}=(1+t)P_0$ donc $1+t = \dfrac{P_{10}}{P_0}\approx \dfrac{3212}{233}\approx 13,7854$
- On veut déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde atteindrait 16000 GW. Pour atteindre cette puissance, les panneaux photovoltaïques occuperaient au sol l'équivalent d'un carré de 400km de côté et suffiraient pour produire toute l'électricité consommée dans le monde (consommation domestique, industrielle et des transports).
- On considère l'algorithme ci-dessous. Recopier et compléter les lignes 3 et 7 afin que cet algorithme réponde à la question posée. $$ \begin{array}{|l |l|}\hline 1/& \text{ Affecter à } N \text{ la valeur } 0 \\ 2/& \text{ Affecter à } P \text{ la valeur } 233\\ 3/& \text{ Tant que } \ldots\\ 4/&\text{ Affecter à } N \text{ la valeur } N +1 \\ 5/&\text{ Affecter à } P \text{ la valeur } P \times 1,30 \\ 6/&\text{ Fin Tant que }\\ 7/& \text{ Afficher } \ldots\\ \hline \end{array} $$ $$ \begin{array}{|l |l|}\hline 1/& \text{ Affecter à } N \text{ la valeur } 0 \\ 2/& \text{ Affecter à } P \text{ la valeur } 233\\ 3/& \text{ Tant que } P< 16\; 000\\ 4/&\text{ Affecter à } N \text{ la valeur } N +1 \\ 5/&\text{ Affecter à } P \text{ la valeur } P \times 1,30 \\ 6/&\text{ Fin Tant que }\\ 7/& \text{ Afficher } 2015+N\\ \hline \end{array} $$
- En faisant tourner cet algorithme complété, déterminer l'année durant laquelle la puissance solaire photovoltaïque installée dans le monde dépasserait 16000 GW. On utilise la calculatrice :
- Proposer une autre méthode, directe et non algorithmique, pour répondre à la question précédente en détaillant la démarche utilisée. $$\begin{array}{ll} P_n> 16 000 &\iff 1,3^n \times 233 > 16 000\\ &\iff 1,3^n > \dfrac{16 000}{233}\\ &\iff n \ln(1,3) > \ln \left(\dfrac{16 000}{233}\right)\\ &\iff n > \dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} \\ \end{array}$$ REMARQUE : Comme $\dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} \approx 16,12$, le plus petit entier $N$ tel que $N>\dfrac{ \ln \left(\dfrac{16 000}{233}\right)}{ \ln (1,3)} $ est $N=17$. On retrouve le résultat de la question précédente.
Conclusion : La puissance solaire photovoltaïque installée dans le monde dépasserait 16000 GW pour la première fois en 2032.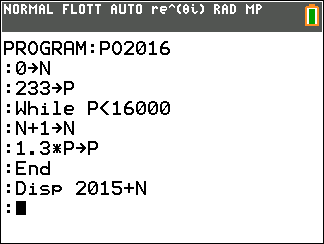
On se propose d'estimer la puissance solaire photovoltaïque installée dans le monde dans les 15 ans à venir, si le taux de croissance annuel reste constant et égal à 30%. On note $P_n$ la puissance solaire photovoltaïque installée dans le monde, en GW, à la fin de l'année $2015 + n$. On a ainsi $P_0 = 233$.
$P_2= P_1 + 30\%\times P_1 = 302,9\times \left(1+\dfrac{30}{100}\right)= 1,3 \times 302,9 \approx 393,8$
On déduit $t\approx 12,79$
Exercice 3 5 points
Deux amis ont monté un atelier associatif pour réparer des vélos. Le but de cette association est que chaque adhérent puisse venir réparer son vélo dans cet atelier avec l'aide d'un spécialiste. Le matériel et les outils sont fournis. Les trois parties de cet exercice peuvent être traitées de manière indépendante
Partie A : les roulements à billes
Nos deux amis commandent régulièrement des lots de $60$ roulements à billes pour les vélos. Ils ont constaté que, lors de leur dernière livraison, sur le lot des $60$ roulements à billes, $3$ étaient défectueux. Ils s'inquiètent donc de la fiabilité du fabricant. Le contrat précise que seulement 4% des pièces sont défectueuses.
- Calculer la fréquence des pièces défectueuses dans le dernier lot. On considère que les pièces constituant ce lot forment un échantillon prélevé de façon aléatoire dans un stock dans lequel 4% des pièces sont défectueuses.
- Déterminer l'intervalle de fluctuation asymptotique à 95% de la fréquence des roulements à billes non conformes dans un échantillon de $60$ roulements. Les valeurs approchées seront arrondies à $10^{-2}$.
On rappelle que l'intervalle de fluctuation asymptotique à 95% sur un échantillon de taille $n$, avec $p$ la proportion de pièces défectueuses sur la population, est : \[\left[p - 1,96\sqrt{\dfrac{p(1 - p)}{p}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{p}}\right]\] - Nos amis ont-ils raison de s'inquiéter ? Justifier votre réponse.
Partie B : les billes
Nos amis se demandent s'ils ne devraient pas plutôt commander des billes pour réparer les roulements évoqués dans la partie A. Ils commandent une grande quantité de billes de 6~mm de diamètre. Malheureusement, certaines présentent un défaut de diamètre. Ils s'aperçoivent qu'ils ne peuvent utiliser que les billes mesurant entre $5,9$ mm et $6,1$ mm. Sur la note du fabricant est indiqué que la variable aléatoire $D$ qui, à chaque bille, lui associe son diamètre, suit la loi normale d'espérance $\mu = 6$ mm et d'écart-type $\sigma = 0,05$ mm.
Question : Calculer la probabilité $P(5,9 \leqslant D \leqslant 6,1)$. Le résultat sera arrondi à $10^{-2}$.
Partie C : les chaînes de vélo
Un tableau est mis à disposition pour permettre aux utilisateurs de savoir quand ils doivent changer leur chaîne de vélo. Par exemple, pour une personne utilisant son vélo en ville $\left(\text{vitesse moyenne } 16~ \text{km.h}^{-1}\right)$ environ 2 heures par jour, la durée de vie moyenne de la chaîne est de 625~jours. On admet que la durée de vie en jour, d'une chaîne de vélo pour un tel utilisateur est une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$. On rappelle que la probabilité que $X$ soit inférieure ou égale à $t$ (exprimé en jour) vaut : $P(X \leqslant t) = 1 - \text{e}^{- \lambda t}$.
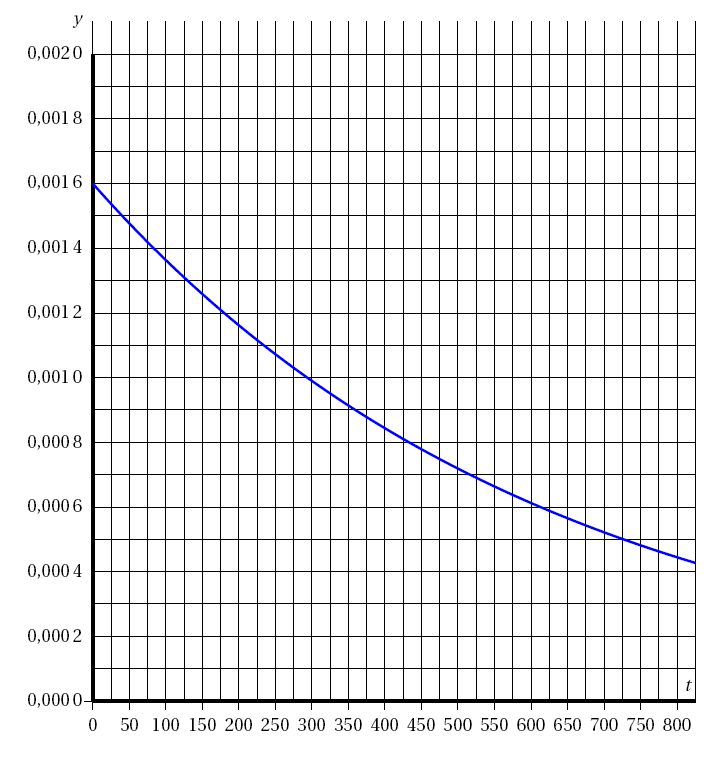
- Démontrer que $\lambda = 0,0016 $.
- Le graphique en ANNEXE 1 représente la fonction de densité de la loi exponentielle de paramètre $\lambda = 0,0016 $ $\left(\text{exprimé en jour}^{-1}\right)$.
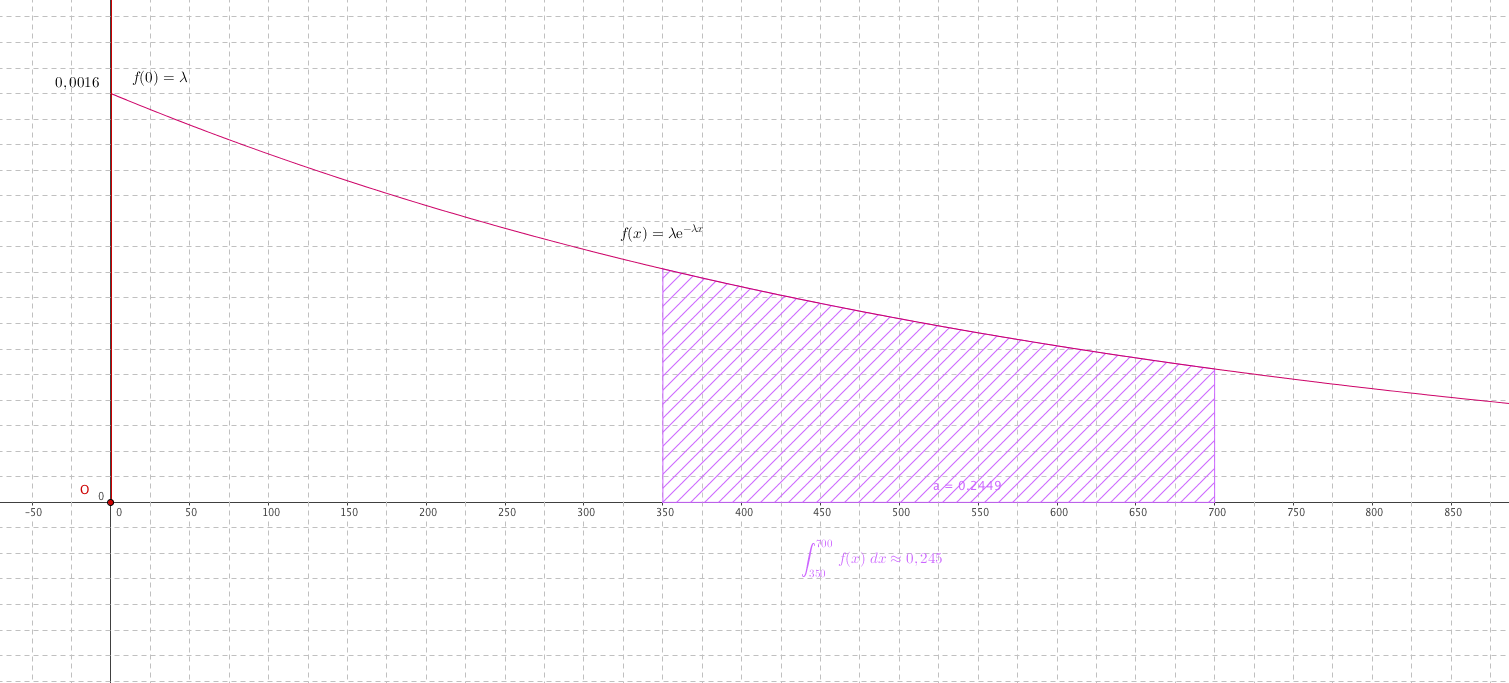
- Représenter sur ce graphique la probabilité que $X$ soit comprise entre 350 jours et 700 jours.
- Calculer la probabilité que $X$ soit comprise entre $350$ jours et $700$ jours. Arrondir le résultat à $10^{-3}$.
- Calculer la probabilité que $X$ soit de moins de $550$ jours. Arrondir à $10^{-3}$.
- Déterminer la valeur de $x$ pour que $P(X < x) = 0,8$. Le résultat sera arrondi à l' unité. Interpréter ce résultat en le resituant dans le contexte.
Annexe à rendre avec la copie
Correction de l'exercice 3 (5 points)
Deux amis ont monté un atelier associatif pour réparer des vélos. Le but de cette association est que chaque adhérent puisse venir réparer son vélo dans cet atelier avec l'aide d'un spécialiste. Le matériel et les outils sont fournis. Les trois parties de cet exercice peuvent être traitées de manière indépendante
Partie A : les roulements à billes
Nos deux amis commandent régulièrement des lots de $60$ roulements à billes pour les vélos. Ils ont constaté que, lors de leur dernière livraison, sur le lot des $60$ roulements à billes, $3$ étaient défectueux. Ils s'inquiètent donc de la fiabilité du fabricant. Le contrat précise que seulement 4% des pièces sont défectueuses.
- Calculer la fréquence des pièces défectueuses dans le dernier lot. On considère que les pièces constituant ce lot forment un échantillon prélevé de façon aléatoire dans un stock dans lequel 4% des pièces sont défectueuses. La fréquence des pièces défectueuses est $f= \dfrac{3}{60}= \dfrac{1}{20}=0,05$
- Déterminer l'intervalle de fluctuation asymptotique à 95% de la fréquence des roulements à billes non conformes dans un échantillon de $60$ roulements. Les valeurs approchées seront arrondies à $10^{-2}$.
On rappelle que l'intervalle de fluctuation asymptotique à 95% sur un échantillon de taille $n$, avec $p$ la proportion de pièces défectueuses sur la population, est : \[\left[p - 1,96\sqrt{\dfrac{p(1 - p)}{p}}~;~p + 1,96\sqrt{\dfrac{p(1 - p)}{p}}\right]\] - Nos amis ont-ils raison de s'inquiéter ? Justifier votre réponse. Comme $f\in I_{60}$ . Nos amis n'ont pas raison de s'inquiéter. L'écart constaté entre le 5% observé dans l'échantillon et e 4% attendu est dû à des fluctuations d'échantillonnage.
- Méthode 1 :
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$ - Méthode 2 :
On remarque que $P(5,9 \leqslant D \leqslant 6,1)= P(\mu-2\sigma \leqslant D \leqslant \mu+2\sigma)\approx 0,954$ d'après un résultat du cours. - Démontrer que $\lambda = 0,0016 $.
- Méthode 1 :
On sait que $E(X)= \dfrac{1}{\lambda}$ donc $\lambda = \dfrac{1}{E(X)} =\dfrac{1}{625}=0,0016$ - Méthode 2 :
La densité d'une loi exponentielle de paramètre $\lambda$ est définie sur $[0; +\infty[$ par $f(x)= \lambda\text{e}^{- \lambda x}$
On a donc $f(0)=\lambda \text{e}^{0}= \lambda$
Par ailleurs on lit graphiquement $f(0)= 0,0016$ , on déduit donc $$\lambda = 0,0016 $$
- Méthode 1 :
- Le graphique en ANNEXE 1 représente la fonction de densité de la loi exponentielle de paramètre $\lambda = 0,0016 $ $\left(\text{exprimé en jour}^{-1}\right)$.
- Représenter sur ce graphique la probabilité que $X$ soit comprise entre 350 jours et 700 jours.
- Calculer la probabilité que $X$ soit comprise entre $350$ jours et $700$ jours. Arrondir le résultat à $10^{-3}$. \begin{align*} P(350\leq X\leq 700) &=\displaystyle\int_{350}^{700} f(x)\; dx \\ &= \displaystyle\int_{350}^{700} \lambda \text{e}^{-\lambda x}\; dx \\ &=\left [ -\text{e}^{-\lambda x}\right ]_{350}^{700}\\ &= -\text{e}^{-700 \lambda }-\left (-\text{e}^{-350 \lambda }\right )\\ &=\text{e}^{-350 \times 0,0016 }-\text{e}^{-700 \times 0,0016 }\\ &\approx 0,245\\ \end{align*}
- Calculer la probabilité que $X$ soit de moins de $550$ jours. Arrondir à $10^{-3}$. \begin{align*} P( X\leq 550) &=\displaystyle\int_{0}^{550} f(x)\; dx \\ &= \displaystyle\int_{0}^{550} \lambda \text{e}^{-\lambda x}\; dx \\ &=\left [ -\text{e}^{-\lambda x}\right ]_{0}^{550}\\ &= -\text{e}^{-550 \lambda }-\left (-\text{e}^{0 }\right )\\ &=1-\text{e}^{-550 \times 0,0016 }\\ &\approx 0,5855\\ \end{align*}
- Déterminer la valeur de $x$ pour que $P(X < x) = 0,8$. Le résultat sera arrondi à l' unité. Interpréter ce résultat en le resituant dans le contexte . On cherche $x$ tel que $P(X < x) = 0,8$
- Résoudre graphiquement sur l'intervalle $[- 1~;~1,5]$ et avec la précision permise par le dessin les deux inéquations suivantes:
- $f(x) \geqslant 1$
- $f'(x) \geqslant 0$.
-
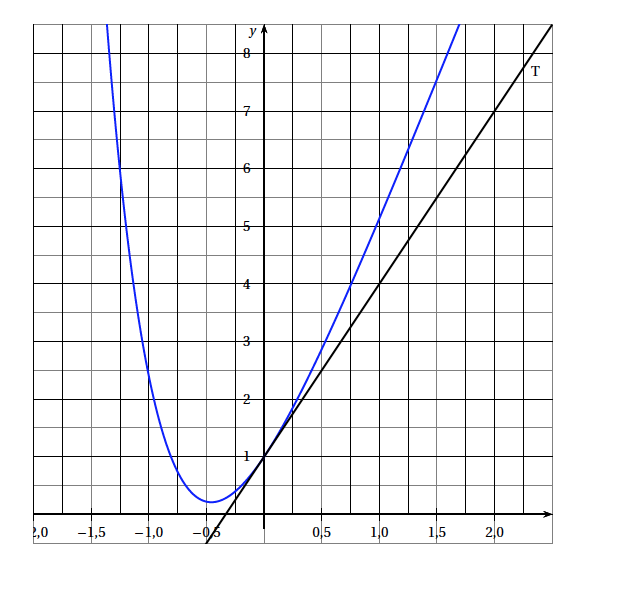
- Donner l'équation. de la tangente T à la courbe $C$ au point de coordonnées (0 ; 1) en sachant que cette tangente passe par le point de coordonnées (2 ; 7).
- En déduire le nombre dérivé $f'(0)$.
- Déterminer, en la justifiant, la limite de $f$ en $+ \infty$. On admet pour la suite que la limite de $f$ en $- \infty$ est $+ \infty$.
- Calculer $f'(x)$ et étudier son signe sur $\mathbb R$.
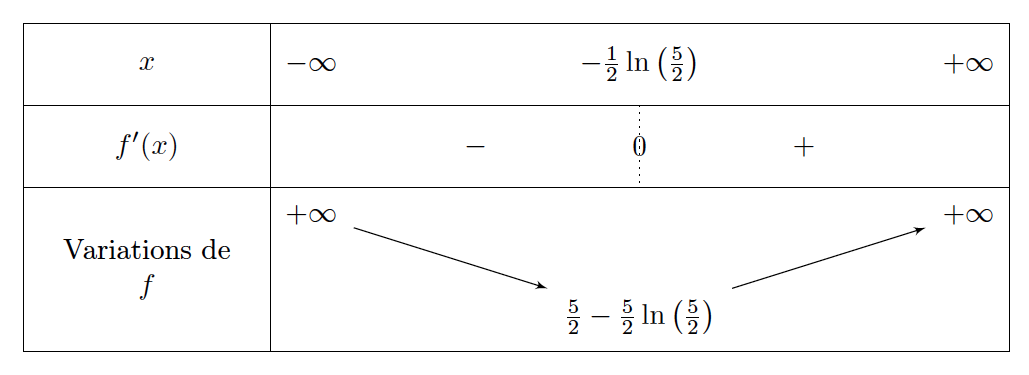
- En déduire le tableau des variations de la fonction $f$ sur $\mathbb R$.
-
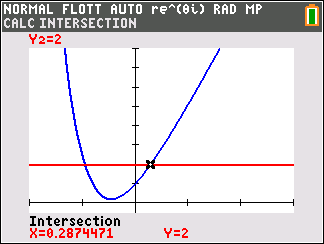
- Déterminer à partir du tableau des variations le nombre de solutions de l'équation $f(x) = 2$.
- Donner une valeur arrondie à $10^{-2}$ près de chaque solution.
- que la courbe $C$ de la partie A est la représentation de la fonction $f$ définie dans la partie B ;
- que la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$.
- Hachurer sur le dessin, en ANNEXE 2, l'aire $\mathcal{A}$ que l'on veut déterminer.
-
- Déterminer une primitive de la fonction $g$ définie sur $\mathbb R$ par : \[\text{pour tout réel }\:x,\: g(x) = \text{e}^{-2x} + 2x - 1.\]
- Justifier que l'aire $\mathcal{A}$ recherchée vaut, en unité d'aire: \[\mathcal{A} = \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\]
- En déduire la valeur exacte puis l'arrondi à $10^{- 2}$ de $\mathcal{A}$.
- Résoudre graphiquement sur l'intervalle $[- 1~;~1,5]$ et avec la précision permise par le dessin les deux inéquations suivantes:
- $f(x) \geqslant 1$ Les solutions de l'inéquation $f(x)\geq 1$ sont les abscisses des points situés au dessus de la droite d'équation $y=1$. On lit àla précision du dessin : $$\mathcal{S}= [-1; -0,8] \cup [0; +\infty[$$
- $f'(x) \geqslant 0$. D'après le graphique $f$ est croissante sur $[x(S); +1,5]$.
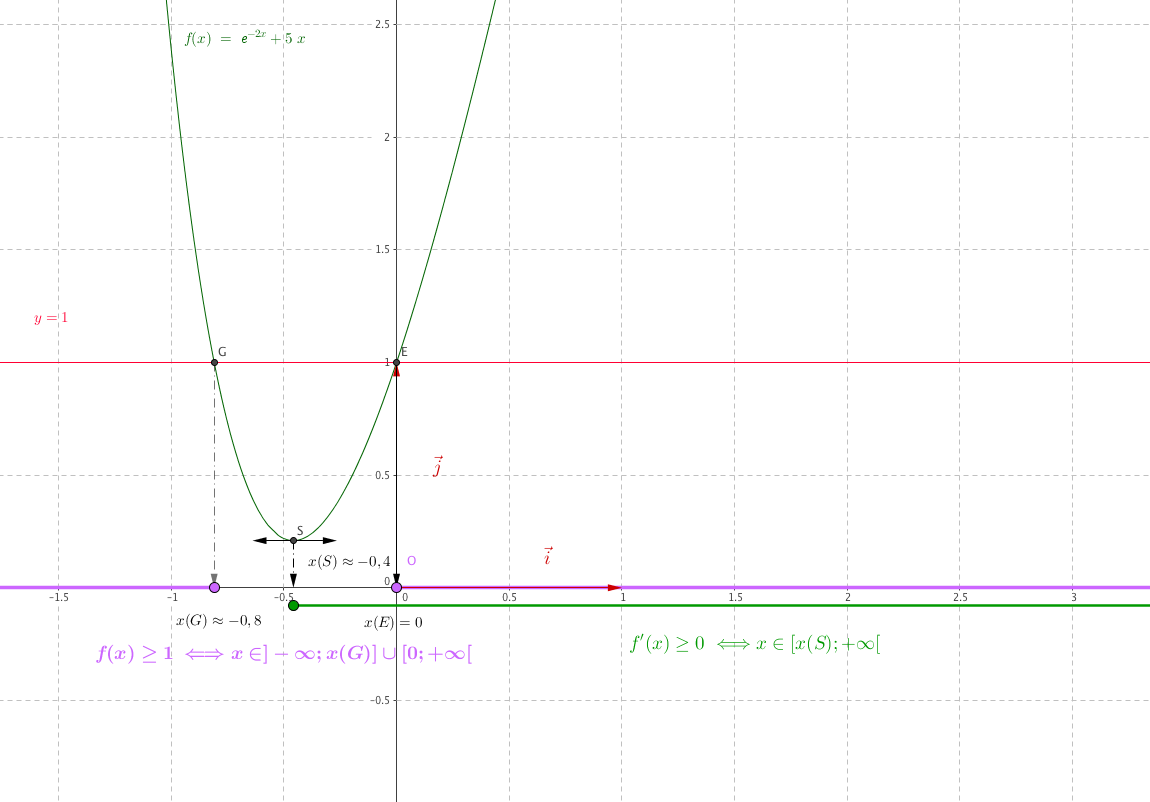
L'ensemble des solutions de l'inéquation $f'(x)\geq 0$ est : $$\mathcal{S}= [-0,4; 1,5]$$ -
- Donner l'équation. de la tangente T à la courbe $C$ au point de coordonnées (0 ; 1) en sachant que cette tangente passe par le point de coordonnées P(2 ; 7). $T$ a une équation du type $y=mx+p$ où \begin{align*} m&=\dfrac{y_P-y_E}{x_P-x_E} \\ &= =\dfrac{4-1}{1-0} \\ &=3\\ \end{align*} Donc $T: y=3x+p$ Comme $E(1,0)\in T$ on déduit $y_E=3x_E+p$ ce qui donne $1=3\times 0 + 1$ soit $p=1$
- En déduire le nombre dérivé $f'(0)$. $f'(0)$ est le coefficient directeur de la tangente $T$ au point d'abscisse 0
d'après la question précédente $f'(0)= 3$. - Déterminer, en la justifiant, la limite de $f$ en $+ \infty$. On admet pour la suite que la limite de $f$ en $- \infty$ est $+ \infty$. $\left.\begin{array}{l} \lim\limits_{-2x \to +\infty} =-\infty\\ \lim\limits_{t \to -\infty}~\text{e}^t=0 \end{array}\right\}$ par composée on obtient: $\lim\limits_{x \to +\infty}\text{e}^{-2x} =0$
- Calculer $f'(x)$ et étudier son signe sur $\mathbb R$. Comme $\left(\text{e}^u\right)'=u'\text{e}^u$, on obtient $$f'(x)=-2\text{e}^{-2x}+5$$ Etudions le signe de la dérivée :
- \begin{align*} f'(x)=0 &\iff -2\text{e}^{-2x}+5=0 \\ &\iff - 2\text{e}^{-2x} =-5 \\ &\iff \text{e}^{-2x} = \dfrac{5}{2}\\ &\iff -2x =\ln\left (\dfrac{5}{2}\right )\\ &\iff x=-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )\\ \end{align*}
- \begin{align*} f'(x)>0 &\iff -2\text{e}^{-2x}+5>0 &\\ &\iff - 2\text{e}^{-2x} >-5 &\\ &\iff \text{e}^{-2x} < \dfrac{5}{2}& \text{en divisant par } -2< 0\\ &\iff -2x < \ln\left (\dfrac{5}{2}\right )&\text{en appliquant } \ln \text{strictement croissante sur }]0; +\infty[\\ &\iff x>-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )&\text{en divisant par } -2< 0 \\ \end{align*}
- En déduire le tableau des variations de la fonction $f$ sur $\mathbb R$. On déduit le tableau de variations de $f$ sur $\mathbb R$:
-
- Déterminer à partir du tableau des variations le nombre de solutions de l'équation $f(x) = 2$. D'après le tableau de variation de $f$ l'équation $f(x)=2$ a deux solutions :
- une notée $x_1$ dans $]-\infty; \alpha]$
- une autre notée $x_2$ dans $[ \alpha; +\infty[$
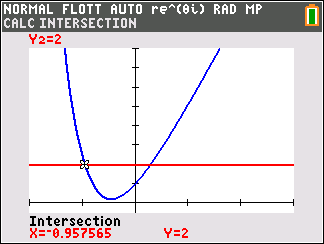
- Donner une valeur arrondie à $10^{-2}$ près de chaque solution. Avec les outils graphiques de la calculatrice on obtient :
- $x_1\approx 0,96 $
- $x_2\approx 0,29$
- que la courbe $C$ de la partie A est la représentation de la fonction $f$ définie dans la partie B ;
- que la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$.
- Hachurer sur le dessin, en ANNEXE 2, l'aire $\mathcal{A}$ que l'on veut déterminer.
-
- Déterminer une primitive de la fonction $g$ définie sur $\mathbb R$ par : \[\text{pour tout réel }\:x,\: g(x) = \text{e}^{-2x} + 2x - 1.\] On utilise deux résultats du cours :
- La primitive d'une somme est la somme des primitives.
- $x\mapsto \text{e}^{ax}$ admat pour primitive $x\mapsto \dfrac{1}{a}\text{e}^{ax}$
- Justifier que l'aire $\mathcal{A}$ recherchée vaut, en unité d'aire: \[\mathcal{A} = \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\] Déterminons tout d'aboerd une équation de T:
- En déduire la valeur exacte puis l'arrondi à $10^{- 2}$ de $\mathcal{A}$.
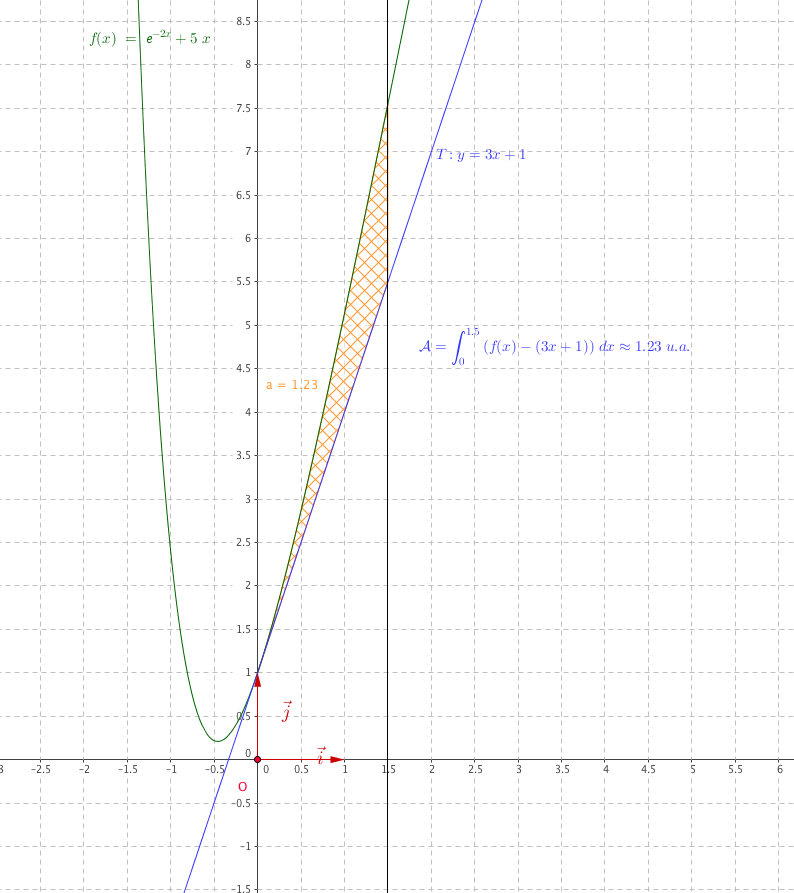
$\begin{align*} \mathcal{A} &= \displaystyle\int_0^{1,5} g(x)\:\text{d}x.\\ &=G(1,5)-G(0)\\ G(1,5)=-\dfrac{1}{2} \text{e}^{-2\times 1,5} + 1,5^2 - 1,5=-\dfrac{1}{2} \text{e}^{-3}+0,75 &\quad G(0)=-\dfrac{1}{2} \text{e}^{-2\times 0} + 0^2 - 0=-0,5\\ \mathcal{A} &= -\dfrac{1}{2} \text{e}^{-3}+0,75+0,5\\ \mathcal{A} &= -\dfrac{1}{2} \text{e}^{-3}+\dfrac{5}{4}\\ &\approx 1,23\end{align*}$
$T: y=f'(0)(x-0)+f(0)$, ici $f(0)=1$ et $f'(0)=3$
On déduit donc : $$T:y=3x+1$$ D'après l'énoncé la courbe $C$ se situe « au-dessus » de la droite tangente T sur $\mathbb R$,
L'aire $\mathcal{A}$ est donc
$$\begin{align*} \mathcal{A} &= \displaystyle\int_0^{1,5} \left(f(x)-y_T\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(f(x)-3x-1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(\text{e}^{-2x} + 5x-3x-1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} \left(\text{e}^{-2x} + 2x -1\right)\:\text{d}x\\ &= \displaystyle\int_0^{1,5} g(x)\:\text{d}x. \end{align*}$$
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique ne sont pas sont réunies !
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
On obtient $I_{60}\approx [ 0; 0,0896]$
Partie B : les billes
Nos amis se demandent s'ils ne devraient pas plutôt commander des billes pour réparer les roulements évoqués dans la partie A. Ils commandent une grande quantité de billes de 6 mm de diamètre. Malheureusement, certaines présentent un défaut de diamètre. Ils s'aperçoivent qu'ils ne peuvent utiliser que les billes mesurant entre $5,9$ mm et $6,1$ mm. Sur la note du fabricant est indiqué que la variable aléatoire $D$ qui, à chaque bille, lui associe son diamètre, suit la loi normale d'espérance $\mu = 6$ mm et d'écart-type $\sigma = 0,05$ mm.
Partie C : les chaînes de vélo
Un tableau est mis à disposition pour permettre aux utilisateurs de savoir quand ils doivent changer leur chaîne de vélo. Par exemple, pour une personne utilisant son vélo en ville $\left(\text{vitesse moyenne } 16~ \text{km.h}^{-1}\right)$ environ 2 heures par jour, la durée de vie moyenne de la chaîne est de 625 jours. On admet que la durée de vie en jour, d'une chaîne de vélo pour un tel utilisateur est une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$. On rappelle que la probabilité que $X$ soit inférieure ou égale à $t$ (exprimé en jour) vaut : $P(X \leqslant t) = 1 - \text{e}^{- \lambda t}$.
On sait que $P(X < x) = 1-\text{e}^{-\lambda x}$ \begin{align*} P( X\leq x) =0,8&\iff 1-\text{e}^{-\lambda x} =0,8 \\ &\iff \text{e}^{-\lambda x} =0,8 \\ &\iff -\lambda x =\ln(0,2) \\ &\iff x=-\dfrac{\ln(0,2)}{\lambda}\\ &\iff x=-\dfrac{\ln(0,2)}{0,0016}\\ &x\approx 1006\\ \end{align*} Il y a 80% de chance que la durée de vie moyenne de la chaîne soit inférieure à 1006 jours.
Exercice 4 6 points
Partie A : Lecture graphique
On considère la courbe $C$ associée à une fonction $f$ représentée en ANNEXE 2 avec la droite T, tangente à la courbe $C$ au point d'abscisse $0$.
Partie B : Étude de la fonction $f$
Soit $f$ la fonction définie sur $\mathbb R$ par la relation $f(x) = \text{e}^{-2x} + 5x$.
Partie C. : Calcul d'aire
On admet :
L'objectif de cette partie est de déterminer par un calcul l'aire $\mathcal{A}$ comprise entre la courbe $C$, la droite T et les droites verticales d'équations $x = 0$ et $x = 1,5$.
Exercice 4 Parties A et C
Exercice 4 6 points
Partie A : Lecture graphique
On considère la courbe $C$ associée à une fonction $f$ représentée en ANNEXE 2 avec la droite T, tangente à la courbe $C$ au point d'abscisse $0$.
Partie B : Étude de la fonction $f$
Soit $f$ la fonction définie sur $\mathbb R$ par la relation $f(x) = \text{e}^{-2x} + 5x$.
$\left.\begin{array}{l} \lim\limits_{x \to +\infty} \text{e}^{-2x} =0\\ \lim\limits_{ x \to +\infty}~5x=+\infty \end{array}\right\}$ par somme on obtient: $\lim\limits_{x \to +\infty} f(x)=+\infty$
$f\left(-\dfrac{1}{2}\ln\left (\dfrac{5}{2}\right )\right ) =f(\alpha)=\text{e}^{-2\alpha} + 5\alpha $
Comme $f'(\alpha)=0$ on déduit $-2\text{e}^{-2\alpha} + 5=0$ donc $ \text{e}^{-2\alpha}=\dfrac{5}{2}$
Ainsi $f(\alpha)=\dfrac{5}{2} - \dfrac{5}{2}\ln\left (\dfrac{5}{2}\right ) $
Partie C. : Calcul d'aire
On admet :
L'objectif de cette partie est de déterminer par un calcul l'aire $\mathcal{A}$ comprise entre la courbe $C$, la droite T et les droites verticales d'équations $x = 0$ et $x = 1,5$.
- Vues: 20536
