Fonction Exponentielle ; des exercices avec corrigé ...
Exercice 1 ![]()

En utilisant la méthode d'Euler, tracer avec un tableur une approximation de la représentation graphique d'une fonction $f$ définie et dérivable sur $[0 ; 2]$ vérifiant : $f'(x)=x^2+x$ et $f(0)=1$.
En utilisant vos connaissances sur les dérivées, rechercher l'expression d'une telle fonction $f$ et comparer sa représentation graphique avec son approximation.

En utilisant la méthode d'Euler, tracer avec un tableur ou une calculatrice une approximation de la courbe d'une fonction $f$ définie et dérivable sur $[-1 ; 1]$, vérifiant : $f'(x)=\dfrac{1}{1+x^2}$ et $f(0)=0$.

- On considère un partage de l'intervalle $[0 ; 1 ]$ en n intervalles de même amplitude $n; (n \in \mtns)$.En utilisant les approximations affines et la méthode d'Euler , donner en fonction de n une approximation de $exp(1/n)$ et $exp(2/n)$ .
- On considère la suite $(u_n)$définie par $u_n=(1+1/n)^n$. Donner à $10^{ -3}$ près les valeurs de $u_n$ obtenues avec une calculatrice pour : $n=10;n=100;n=1000;n=10 000; n=100 000$.
- En déduire une valeur approchée de $exp(1)$.

Écrire plus simplement : $$\begin{array}{ll}\\1. \quad e^{2x}\times e^{1-2x} &2. \quad \dfrac{e^{2x+3}}{e^{x-1}} \\3. \quad (e^x+e^{-x})^2&4. \quad e^{-2x}-\dfrac{e^{2x}+1}{e^{2x}} \end{array} $$

Soit $f$ définie sur $\mtr$ par $f(x)=\left(e^x+e^{x}\right)^2-\left(e^x-e^{-x}\right)^2$. Montrer que $f$ est une fonction constante sur $\mtr$.

On considère la fonction $f$ définie sur $\mtr$ par : $f(x)=x-\dfrac{e^x-1}{e^x+1}$ .
- Vérifier que pour tout réel $x$ : $f(x)=x-\dfrac{1-e^{-x}}{1+e^{-x}}$
- Montrer que $f(x)=x-1+\dfrac{2}{e^x+1}$ ;
- Montrer que $f(x)=x+1-\dfrac{2}{e^{-x}+1}$
- Montrer que $ f$ est dérivable sur $\mtr$ , vérifier que :$f'(x)=\dfrac{e^{2x}+1}{(e^x+1)^2}=\dfrac{1+e^{-2x}}{(e^{-x}+1)^2}$ .
Exercice 8 ![]()

Résoudre dans $\mtr$ les inéquations suivantes :
- $e^{2x-1}>1$
- $e^x-e^{2x}\geq 0$ ;
- $e^{2x+5}<e^{1-x}$.
 Déterminer les limites suivantes : $$\begin{array}{ll} 1. \quad \dis\lim_{x\to +\infty}3xe^{-x}& 2 . \quad \dis\lim_{x\to -\infty}(x+1)e^x\\ 3.\quad \dis\lim_{x\to +\infty}\dfrac{2e^x-5}{3x}& 4. \quad \dfrac{e^x-1}{x^3}\\ 5. \quad \dis\lim_{x\to -\infty}\dfrac{e^x+e^{-x}}{3+e^x}& \end{array}$$
Déterminer les limites suivantes : $$\begin{array}{ll} 1. \quad \dis\lim_{x\to +\infty}3xe^{-x}& 2 . \quad \dis\lim_{x\to -\infty}(x+1)e^x\\ 3.\quad \dis\lim_{x\to +\infty}\dfrac{2e^x-5}{3x}& 4. \quad \dfrac{e^x-1}{x^3}\\ 5. \quad \dis\lim_{x\to -\infty}\dfrac{e^x+e^{-x}}{3+e^x}& \end{array}$$ Déterminer les limites suivantes : $$\begin{array}{ll} 1. \quad \dis\lim_{x\to +\infty}e^{x^2-3x-5}& 2 . \quad \dis\lim_{x\to -\infty}e^{x^2-3x-5}\\ 3.\quad \dis\lim_{x\to +\infty}2+3e^{-x^2+1}& 4. \quad \dis\lim_{x\to -\infty}\dfrac{ e^x-3}{e^x+2}\\5. \quad \dis\lim_{x\to 0}\dfrac{ e^x+1}{e^{2x}} & \end{array}$$
Déterminer les limites suivantes : $$\begin{array}{ll} 1. \quad \dis\lim_{x\to +\infty}e^{x^2-3x-5}& 2 . \quad \dis\lim_{x\to -\infty}e^{x^2-3x-5}\\ 3.\quad \dis\lim_{x\to +\infty}2+3e^{-x^2+1}& 4. \quad \dis\lim_{x\to -\infty}\dfrac{ e^x-3}{e^x+2}\\5. \quad \dis\lim_{x\to 0}\dfrac{ e^x+1}{e^{2x}} & \end{array}$$
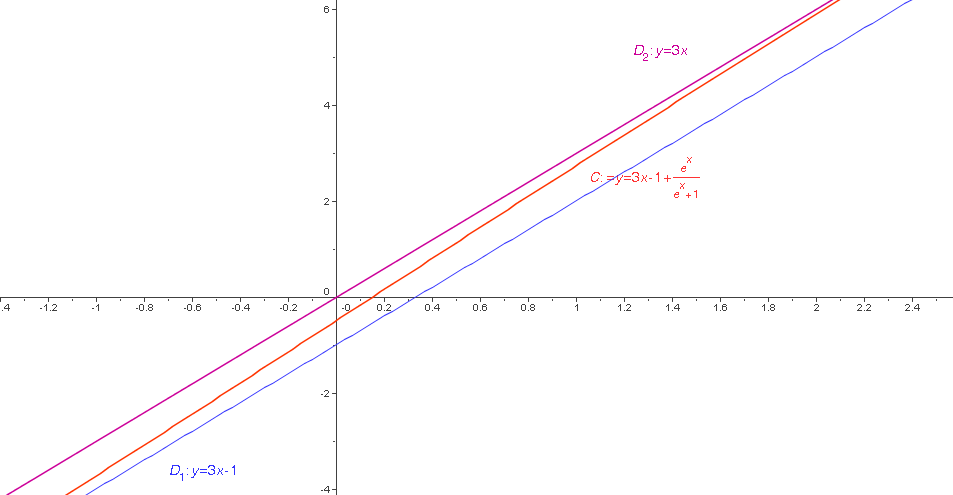
Soit $(C)$ la courbe de la fonction $f$ définie sur $\mtr$ par : $f(x)=3x-1+\dfrac{e^x}{e^x+1}$ .
Démontrer que $(C)$ a deux asymptotes obliques dont on donnera une équation.

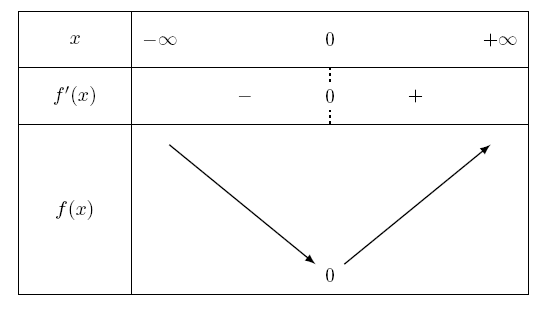
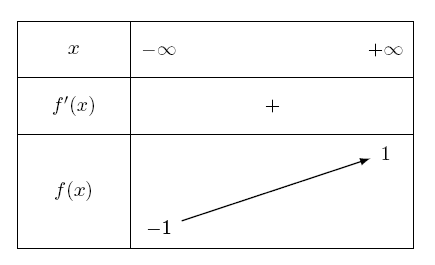
- Étudier les variations de la fonction $f$ définie sur $\mtr$ par $f(x)=\dfrac{e^{ 2x }-1}{e^{ 2x }+1 }$.
- Dresser son tableau de variations. Soit $\mathcal{C}$ la courbe représentative de $f$ .
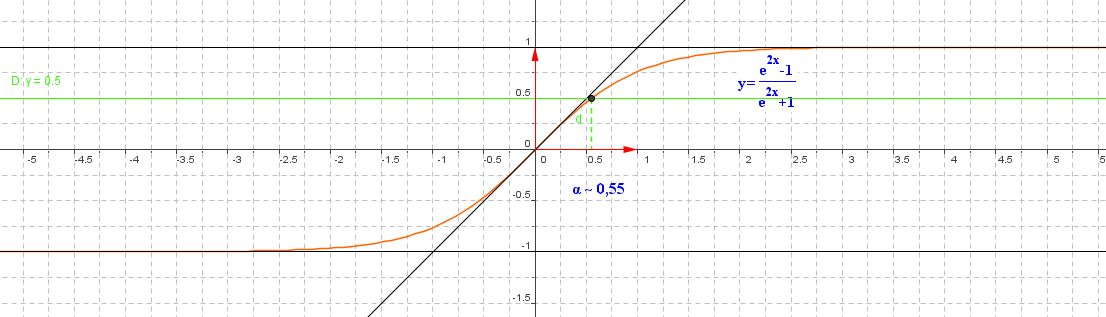
- Donner l'équation de la tangente $T$ à $\mathcal{C}$ au point d'abscisse 0. Tracer $\mathcal{C}$ et $T$.
- Démontrer que l'équation $f(x)=\dfrac{1}{2}$ a une solution unique $\alpha$ dans $\mtr$ . Donner une valeur approchée de $\alpha$ .

Résoudre dans $\mtr$ les équations suivantes :
$$\begin{array}{ll} 1. \quad e^{2x+1}-1=0& 2 . \quad e^{x+1}-e^{2x-3}=0 \\ 3.\quad e^{x-1}\times e^{3x+5}=1& 4. \quad e^{2x}+e^x-2=0\\ 5. \quad\dfrac{2e^x+1}{e^x}=2e^3+e^{-x} &\\\end{array}$$
Justifier que chacune des fonctions est dérivable sur $\mtr$ , calculer la dérivée et étudier le signe de cette dérivée.
$$\begin{array}{ll} 1. \quad f(x)=e^{2x^2+1}& 2 . \quad g(x)=(2x+1)e^{2x+1} \\ 3.\quad h(x)=\dfrac{ e^x-e^{-x}}{ 2}& 4. \quad t(x)=\dfrac{3e^x}{e^{2x}+1} \end{array}$$
- Vues: 4666