Exercices sur le chapitre continuité : des corrections
Exercice 01
Donner une valeur approchée à $10^ {-2}$ près de cette solution.
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = [\2 ; \3]$.
- $\1$ est strictement croissante sur l' intervalle $I = [\2 ; \3]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
$\6$ est compris entre $\1\left(\2\right)$ et $\1\left(\3\right)$, en effet $\1\left(\2\right) < \6 $ et $\1\left(\3\right) > \6 $
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $[\2 ; \3]$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$
Exercice 02
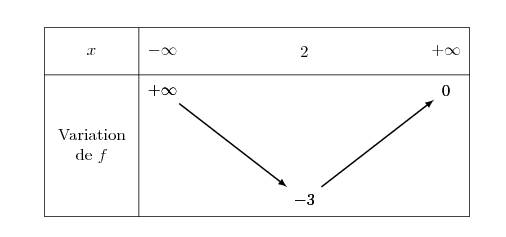
On donne ci-contre le tableau de variations de $f$.
Quel est le nombre de solutions de l'équation $f(x) = 1 $
(On justifiera le résultat)
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\1 \left(\3\right)=\5$
$\6\in \left[\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right]$ .
Exercice 03
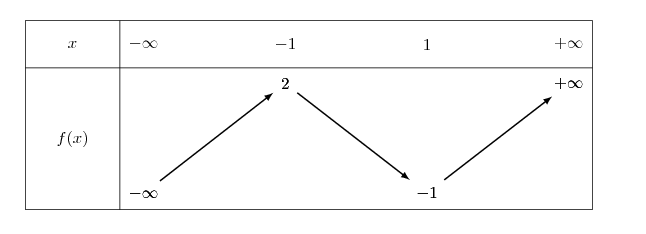
- Quel est le nombre de solutions de l'équation $f(x) = 0$
- \(\1 \) est une fonction dérivable (donc continue) sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\1\) est strictement croissante sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\lim\limits_{x \to \2}~\1(x)=\4\) et \(\1 \left(\3\right)=\5\)
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
- $\1 $ est une fonction dérivable donc continue sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1 \left(\2\right)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- Quel est le nombre de solutions de l'équation $f(x) = - 5$
(On justifiera les résultats)
- \(\1 \) est une fonction dérivable (donc continue) sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\1\) est strictement croissante sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\lim\limits_{x \to \2}~\1(x)=\4\) et \(\1 \left(\3\right)=\5\)
D'après le théorème de la bijection :
\(\1\) réalise donc une bijection de \(\left]\2 ; \3\right]\) sur \(\left]\4;\5\right]\)
\(\6\in \left]\4;\5\right]\),
donc l'équation \(\1(x) = \6 \) a une racine unique \(\7\) dans \(\left]\2 ; \3\right]\) .
$\6$ est compris entre $\5$ et $\4$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right]$ .
$\6\in \left[\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right[$ .
D'après le théorème de la bijection :
\(\1\) réalise donc une bijection de \(\left]\2 ; \3\right]\) sur \(\left]\4;\5\right]\)
\(\6\in \left]\4;\5\right]\),
donc l'équation \(\1(x) = \6 \) a une racine unique \(\7\) dans \(\left]\2 ; \3\right]\) .
Sur $[-1; +\infty[$, $f$ présente un minimum absolu en $1$ qui vaut $-1$, donc pour tout réel $x$ de $[-1; +\infty[$ on a $f(x)\geq -1$,
donc l'équation $f(x) = - 5$ n'a pas de solution sur $[-1; +\infty[$.
Exercice 04
Une figure ?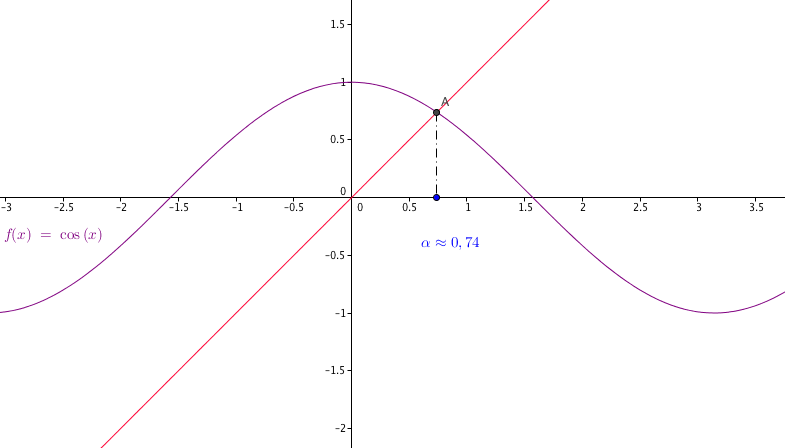
- Montrer que si $x$ est solution de $(E)$ alors $0\leq x\leq\dfrac{\pi}{2} $ . Tout d'abord comme pour tout réel $x$ on a : $-1\leq \cos x \leq 1 $; et comme $\cos x = x$ , on déduit qu'une solution de $(E)$ est nécessairement dans $[-1; 1]$.
- Montrer que l'équation $(E)$ a une solution unique $\alpha$ dans $\mathbb{R}$ . Déjà si $(E)$ a une solution alors celle-ci est nécessairement dans l'intervalle $\left[0; \dfrac{\pi}{2}\right]$. $$(E) \Leftrightarrow \cos x - x=0$$ Notons $f$ la fonction définie sur $\left[0; \dfrac{\pi}{2}\right]$ par $f(x)= \cos x - x $
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left[\2 ; \3\right]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
Par ailleurs si $x\in [-1;0[$ on a $-\dfrac{\pi}{2} < -1 < x < 0$, on lit sur le cercle trigonométrique $\cos x \geq 0$
Donc $(E)$ n'a pas de solution sur $[-1;0[$
$f$ est dérivable sur $\left[0; \dfrac{\pi}{2}\right]$ et $f'(x)= -\sin x - 1 $
Pour tout réel $x$; on a : \begin{align*} -1 \leq \sin x \leq 1& \\ 1 \geq -\sin x \geq -1& \text{ en multipliant par } -1 < 0\\ -1 \leq -\sin x \leq 1& \\ -2 \leq -\sin x -1\leq 0&\text{ en ajoutant } -1 \\ f'(x)\leq 0 & \\ \end{align*} Par ailleurs comme $f'(x)=0\Leftrightarrow -\sin x -1=0\Leftrightarrow \sin x= -1 \Leftrightarrow x = -\dfrac{\pi}{2} = k 2 \pi$
Ainsi la dérivée de $f$ est strictement négative sauf en des valeurs isolées où elle s'annule, donc $f$ est strictement décroissante sur $\left[0; \dfrac{\pi}{2}\right]$.
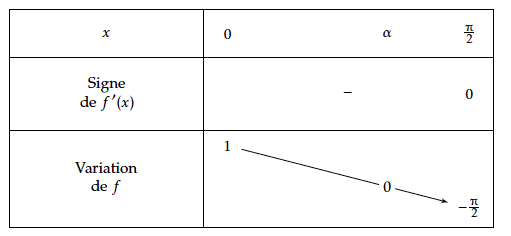
$\6$ est compris entre $\5$ et $\4$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right]$ .
- Déterminer une valeur approchée de $\alpha$ à $10 ^{-2}$ près par défaut.
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right) > \8 > \3\left(\6\right)$, soit $\3\left(\4\right)> \3\left(\1\right)>\3\left(\6\right)$
comme $\3$ est strictement décroissante sur $\left[\9;\10\right]$; on déduit $\4< \1 < \6$
Exercice 05
et $(C')$ la courbe représentative de la fonction $g$ définie sur $ [0 ; +\infty [$ par $ g(x) =\sqrt{3x}$ .
Quel est le nombre de points d'intersections de $(C)$ et de $(C')$ ? (Justifier)
Une figure ?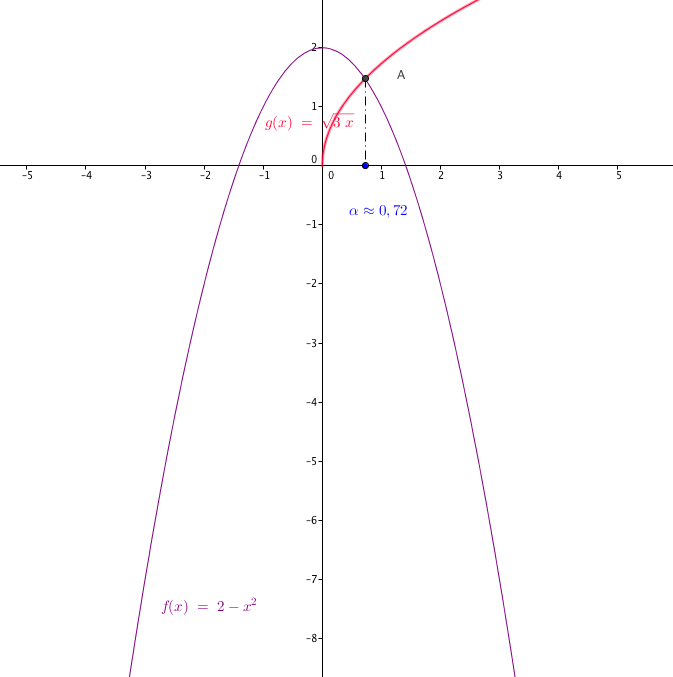
On résout $f(x)= g(x)\rightarrow 2-x^2-\sqrt{3x}=0$
On note $h: x\mapsto 2-x^2-\sqrt{3x}$
$h$ est dérivable sur $]0; +\infty[$ et $h'(x)= -2x-\dfrac{3}{2\sqrt{3x}}$
Comme ici $x>0$; on a clairement $h'(x)<0$ comme somme de deux réels strictement négatifs.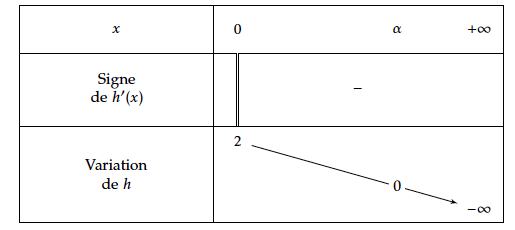
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
$ \6 \in \left]\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right[$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right) > \8 > \3\left(\6\right)$, soit $\3\left(\4\right)> \3\left(\1\right)>\3\left(\6\right)$
comme $\3$ est strictement décroissante sur $\left[\9;\10\right]$; on déduit $\4< \1 < \6$
Exercice 06
Une figure ?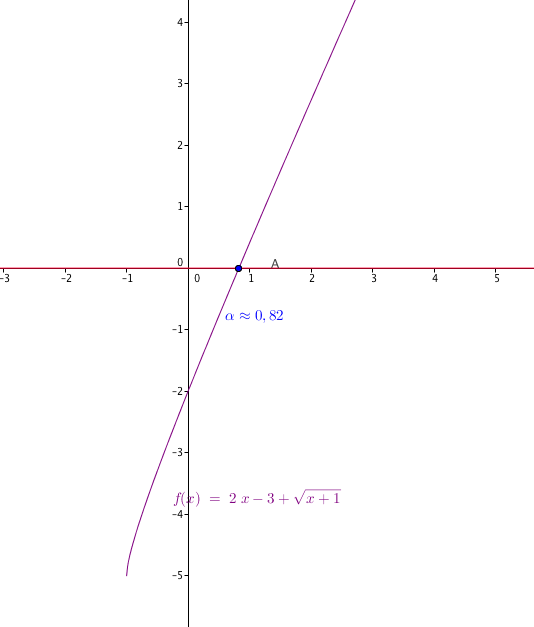
- Donner le tableau de variations de $h$ .
- En déduire que l'équation $h(x) = 0$ a une solution unique $\alpha$ dans $[- 1 ; +\infty [$ .
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- Donner une valeur approchée de $\alpha$ à $ 10 ^{-2}$ près. (Facultatif : donner la valeur exacte de $\alpha$ )
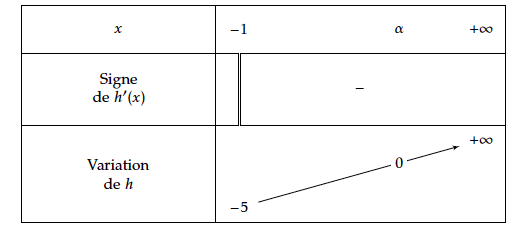
$\1$ réalise donc une bijection de $\left]\2 ; \3\right[$ sur $\left]\4;\5\right[$
$\6\in \left]\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right[$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès : Avec une calculatrice on obtient : $\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$
Exercice 07
Dans les exemples qui suivent; dénombrer les solutions des équations dans un intervalle $I$ et en donner un encadrement d'amplitude $10^{-2}$.
- $x^3+5x=2$, $I=[0;1]$. Soit $f: x\mapsto x^3+5x$
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = [\2 ; \3]$.
- $\1$ est strictement croissante sur l' intervalle $I = [\2 ; \3]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
- $x^5-5x+1=0$, $I=[-2;2]$. Soit $f: x\mapsto x^5-5x+1$
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = [\2 ; \3]$.
- $\1$ est strictement croissante sur l' intervalle $I = [\2 ; \3]$.
- $\1\left(\2\right)=\4$ et $\1\left(\3\right)=\5$
$\6$ est compris entre $\1\left(\2\right)$ et $\1\left(\3\right)$, en effet $\1\left(\2\right) < \6 $ et $\1\left(\3\right) > \6 $
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $[\2 ; \3]$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$
$$f'(x)=5x^4-5=5(x^4-1)=5(x^2-1)(x^2+1)= 5(x -1)(x+1)(x^2+1)$$
$\6$ est compris entre $\1\left(\2\right)$ et $\1\left(\3\right)$, en effet $\1\left(\2\right) < \6 $ et $\1\left(\3\right) > \6 $
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $[\2 ; \3]$ .
- \(\1 \) est une fonction dérivable (donc continue) sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\1\) est strictement croissante sur l' intervalle \(I = \left]\2 ; \3\right]\).
- \(\lim\limits_{x \to \2}~\1(x)=\4\) et \(\1 \left(\3\right)=\5\)
- $\1 $ est une fonction dérivable donc continue sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1 \left(\2\right)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- $x+\dfrac{4}{x^2}=\dfrac{9}{2}$, $I=[1;4]$.
- $2x\sqrt{x+2}=-1$, $I=[2;+\infty]$. Clairement cette équation n'a pas de solution, car sur $I=[2;+\infty]$, on a $x\geq 2 > 0$ et de même $\sqrt{x+2} >0$, par produit on a donc $2x\sqrt{x+2} > 0$ et donc ne peut pas égal à -1 !
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right) > \8 > \3\left(\6\right)$, soit $\3\left(\4\right)> \3\left(\1\right)>\3\left(\6\right)$
comme $\3$ est strictement décroissante sur $\left[\9;\10\right]$; on déduit $\4< \1 < \6$
D'après le théorème de la bijection :
\(\1\) réalise donc une bijection de \(\left]\2 ; \3\right]\) sur \(\left]\4;\5\right]\)
\(\6\in \left]\4;\5\right]\),
donc l'équation \(\1(x) = \6 \) a une racine unique \(\7\) dans \(\left]\2 ; \3\right]\) .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$
$\6\in \left[\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right[$ .
Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$
- Vues: 5119
