Baccalauréat S Pondichéry 4 mai 2018 - Correction Exercice 2
Page 4 sur 10
Correction de l'exercice 2 (4 points)
Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$.
Les points A, B et C ont pour affixes respectives $a = - 4,\: b = 2$ et $c = 4$.
- On considère les trois points A$'$, B$'$ et C$'$ d'affixes respectives $a'= \text{j}a$, $b'= \text{j}b$ et $c'= \text{j}c$ où j est le nombre complexe $-\dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$.
- Donner la forme trigonométrique et la forme exponentielle de j. En déduire les formes algébriques et exponentielles de $a'$, $b'$ et $c'$. $|j|=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}}=1$
- Les points A, B et C ainsi que les cercles de centre O et de rayon 2, 3 et 4 sont représentés sur le graphique fourni ci-dessous.
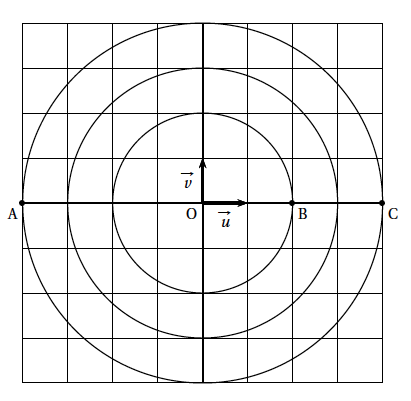
Placer les points A$'$, B$'$ et C$'$ sur ce graphique.
$j=\cos \left(\dfrac{2\pi}{3}\right)+\sin \left(\dfrac{2\pi}{3}\right) =\text{e}^{2 \text{i}\pi/3}$.
$\quad$
Ainsi
$\begin{align*} a’&=-4j \\
&=2-2 \text{i}\sqrt{3}\quad \text{forme algébrique}\\
&=-4\text{e}^{2 \text{i} \pi/3} \\
&=4\text{e}^{2 \text{i} \pi/3+ \text{i}\pi} \\
&=4\text{e}^{5 \text{i}\pi/3} \quad \text{forme exponentielle}
\end{align*}$
$b’=-1+ \text{i}\sqrt{3}$ et $c’=-2+2 \text{i}\sqrt{3}$ $\quad$ Formes algébriques.
$b’= 2j=2\text{e}^{2 \text{i}\pi/3}$ et $c’=4j=4\text{e}^{2 \text{i}\pi/3}$ $\quad$ Formes exponentielles.
$\quad$
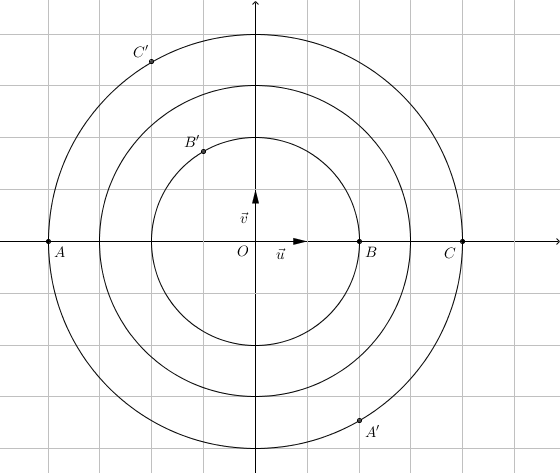
- Montrer que les points A$'$, B$'$ et C$'$ sont alignés. Calculons :
- On note M le milieu du segment [A$'$C], N le milieu du segment [C$'$C] et P le milieu du segment [C$'$A]. Démontrer que le triangle MNP est isocèle. L’affixe de $M$ est :
$\begin{align*} \dfrac{b’-a’}{c’-a’} &=\dfrac{2j+4j}{4j+4j} \\
&=\dfrac{6}{8} \\
&=\dfrac{3}{4}
\end{align*}$
Ainsi un argument de $\dfrac{b’-a’}{c’-a’}$ est $0$.
Les points $A’,B’$ et $C’$ sont donc alignés.
$\begin{align*} m&=\dfrac{c+a’}{2}\\
&=\dfrac{4-4j}{2}\\
&=2-2j\\
&=2+1- \text{i}\sqrt{3} \\
&=3- \text{i}\sqrt{3}
\end{align*}$.
L’affixe de $N$ est :
$\begin{align*} n&=\dfrac{c+c’}{2} \\
&=\dfrac{4+4j}{2}\\
&=2+2j\\
&=2-1+ \text{i}\sqrt{3} \\
&=1+ \text{i}\sqrt{3}\end{align*}$.
L’affixe de $P$ est :
$\begin{align*} p&=\dfrac{c’+a}{2} \\
&=\dfrac{4j-4}{2} \\
&=2j-2 \\
&=-1+ \text{i}\sqrt{3}-2 \\
&=-3+ \text{i}\sqrt{3}
\end{align*}$.
Ainsi l’affixe du vecteur $\vec{PN}$ est $z_1=1+ \text{i}\sqrt{3}-\left(-3+ \text{i}\sqrt{3}\right)=4$.
Ainsi $PN=4$
et l’affixe du vecteur $\vec{NM}$ est $z_2=3- \text{i}\sqrt{3}-\left(1+ \text{i}\sqrt{3}\right)=2-2 \text{i}\sqrt{3}$
Ainsi $NM=\sqrt{2^2+\left(2\sqrt{3}\right)^2}=4$.
Le triangle $MNP$ est donc isocèle en $N$.
- Vues: 30328
